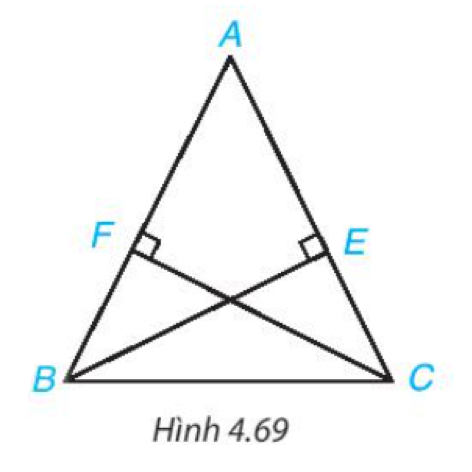
Bài 4.23 trang 84 Toán lớp 7: Cho tam giác ABC cân tại A và các điểm E, F lần lượt nằm trên các cạnh AC, AB sao cho BE vuông góc với AC, CF vuông góc với AB (H.4.69). Chứng minh rằng BE = CF.
Phương pháp giải:
Lời giải:
Do tam giác ABC cân tại A nên: (tính chất tam giác cân)
Xét 2 tam giác vuông BFC và CEB:
BC chung
=>(cạnh huyền – góc nhọn)
=>BE=CF (2 cạnh tương ứng).
Bài 4.24 trang 84 Toán lớp 7: Cho tam giác ABC cân tại A và M là trung điểm của đoạn thẳng BC. Chứng minh AM vuông góc với BC và AM là tia phân giác của góc BAC.
Phương pháp giải:
Lời giải:
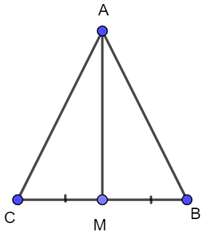
Xét 2 tam giác AMC và AMB có:
AM chung
AB=AC (do tam giác ABC cân tại A)
MB=MC (gt)
AMB=AMC(c.c.c)
(2 góc tương ứng)
AM là phân giác của góc BAC
Mặt khác: (2 góc tương ứng) mà ( 2 góc kề bù)
Nên: .
Vậy AM vuông góc với BC.
Bài 4.25 trang 84 Toán lớp 7: Cho tam giác ABC và M là trung điểm của đoạn thẳng BC.
a) Giả sử AM vuông góc với BC. Chứng minh rằng tam giác ABC cân tại A.
b) Giả sử AM là tia phân giác của góc BAC. Chứng minh rằng tam giác ABC cân tại A.
Phương pháp giải:
a) Chứng minh tam giác hai tam giác AMB và AMC bằng nhau Tam giác ABC cân.
b) Từ M kẻ hai đường vuông góc với AC và AB từ đó chứng minh hai góc B và C bằng nhau.
Chứng minh hai tam giác AMB và AMC bằng nhau
Tam giác ABC cân
Lời giải:
a)
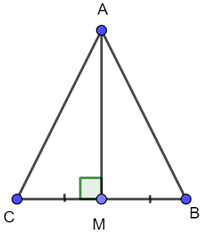
Xét 2 tam giác vuông AMC và AMB có:
AM chung
BM=CM (gt)
=> (c.g.c)
=> AM=BM (2 cạnh tương ứng)
=> Tam giác ABM cân tại A
b)
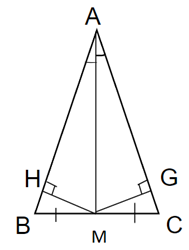
Kẻ MH vuông góc với AB(H thuộc AB)
MG vuông góc với AC (G thuộc AC)
Xét 2 tam giác vuông AHM và AGC có:
AM chung
=>(cạnh huyền – góc nhọn)
=>HM=GM (2 cạnh tương ứng)
Xét 2 tam giác vuông BHM và CGM có:
BM=CM(gt)
MH=MG(cmt)
=>(cạnh huyền – cạnh góc vuông)
=>(2 góc tương ứng)
=>Tam giác ABC cân tại A.
Bài 4.26 trang 84 Toán lớp 7: Tam giác vuông có hai cạnh bằng nhau được gọi là tam giác vuông cân. Hãy giải thích các khẳng định sau:
a) Tam giác vuông cân thì cân tại đỉnh góc vuông;
b) Tam giác vuông cân có hai góc nhọn bằng 45°;
c) Tam giác vuông có một góc nhọn bằng 45° là tam giác vuông cân.
Phương pháp giải:
Lời giải:
a)Do tổng ba góc trong 1 tam giác bằng 180 độ nên tam giác không thể có 2 góc vuông
=>Tam giác vuông cân sẽ có 2 góc nhọn bằng nhau
=> Tam giác vuông cân thì cân tại đỉnh góc vuông.
b) Giả sử hai góc nhọn trong tam giác vuông là x, ta có:
Vậy tam giác vuông cân có hai góc nhọn bằng 45°.
a) Gọi góc còn lại của tam giác vuông có 1 góc nhọn bằng 45° là x, ta có:
Vậy tam giác vuông có một góc nhọn bằng 45° là tam giác vuông cân.
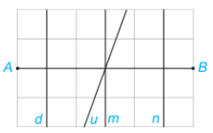
Bài 4.27 trang 84 Toán lớp 7: Trong Hình 4.70, đường thẳng nào là đường trung trực của đoạn thẳng AB?
Phương pháp giải:
Lời giải:
Quan sát hình 4.70 ta thấy đường thẳng m vuông góc với đoạn thẳng AB tại trung điểm của AB nên m là đường trung trực của AB.
Bài 4.28 trang 84 Toán lớp 7: Cho tam giác ABC cân tại A có đường cao AD. Chứng minh rằng đường thẳng AD là đường trung trực của đoạn thẳng BC.
Phương pháp giải:
Chứng minh 2 tam giác bằng nhau suy ra 2 cạnh tương ứng bằng nhau, 2 góc tương ứng bằng nhau
Chú ý: Hai góc kề bù bằng nhau thì mỗi góc bằng 90 độ
Lời giải:
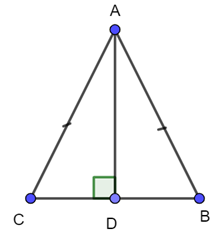
Do tam giác ABC cân tại A nên AB = AC,
Do AD là đường cao của tam giác ABC hay AD ⊥ BC tại D nên tam giác ABD vuông tại D và tam giác ACD vuông tại D.
Xét hai tam giác ABD vuông tại D và tam giác ACD vuông tại D có:
AB = AC (chứng minh trên).
(chứng minh trên).
Do đó (cạnh huyền – góc nhọn).
Khi đó BD = CD (2 cạnh tương ứng) hay D là trung điểm của đoạn thẳng BC.
Do AD vuông góc với BC tại trung điểm của BC nên AD là đường trung trực của đoạn thẳng BC.
Vậy đường thẳng AD là đường trung trực của đoạn thẳng BC.
Xem thêm các bài giải Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
