Với giải sách bài tập Toán 7 Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:
Giải SBT Toán lớp 7 Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng
Hướng dẫn giải
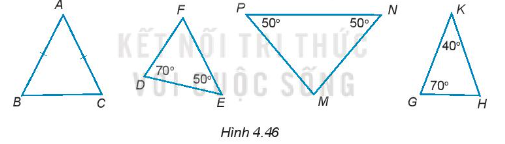
+ Tam giác ABC có AB = AC (kí hiệu bằng nhau trên hình)
Do đó, tam giác ABC cân tại đỉnh A.
+ Áp dụng định lí tổng 3 góc trong tam giác DEF, ta có:
Suy ra .
Do đó ta có, . Vậy tam giác DEF không phải tam giác cân.
+ Tam giác MNP có .
Do đó, tam giác MNP cân tại đỉnh M.
+ Áp dụng định lí tổng 3 góc trong tam giác KGH, ta có:
Suy ra .
Do đó tam giác KGH có .
Vậy tam giác KGH cân tại đỉnh K.
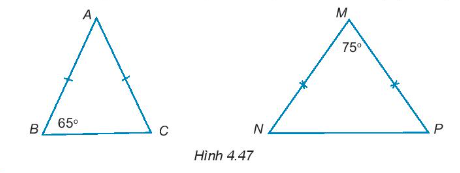
Bài 4.42 trang 68 Toán 7 Tập 1: Tính số đo các góc còn lại trong các tam giác cân dưới đây (H.4.47).
Hướng dẫn giải
+ Tam giác ABC có AB = AC nên tam giác ABC cân tại đỉnh A.
Suy ra .
Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:
Suy ra .
+ Tam giác MNP có MN = MP nên tam giác MNP cân tại đỉnh M.
Suy ra .
Áp dụng định lí tổng ba góc trong tam giác MNP, ta có:
.
Vậy .
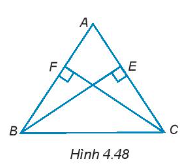
Hướng dẫn giải
Tam giác ABE vuông tại E, do đó:
.
Tam giác ACF vuông tại F, do đó:
.
Từ đó, suy ra .
Xét tam giác vuông AEB và tam giác vuông AFC có:
BE = CF (theo giả thiết)
(cmt)
Do đó, ∆AEB = ∆AFC (cạnh góc vuông và góc nhọn kề nó).
Suy ra AB = AC (hai cạnh tương ứng).
Vậy tam giác ABC cân tại đỉnh A.
a) ∆ABD vuông tại B.
b) ∆ABD = ∆BAC.
c) Các tam giác AMB, AMC là các tam giác cân tại đỉnh M.
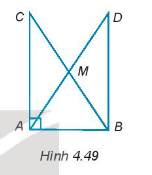
Hướng dẫn giải
a) Xét tam giác AMC và tam giác DMB có:
MA = MD (gt)
MB = MC (M là trung điểm của BC)
(hai góc đối đỉnh)
Do đó, ∆AMC = ∆DMB (c – g – c).
Suy ra (hai góc tương ứng).
Do tam giác ABC vuông tại A nên .
Khi đó, ta có: = .
Suy ra .
Vậy tam giác ABD vuông tại B.
b) Xét tam giác vuông ABD và tam giác vuông BAC có:
BD = AC (do ∆AMC = ∆DMB)
AB: cạnh chung
Do đó, ∆ABD = ∆BAC (hai cạnh góc vuông).
c) Do tam giác ABC vuông tại A nên AC ⊥ AB tại A.
Tam giác ABD vuông tại B nên DB ⊥ AB tại B.
Suy ra AC // DB (do cùng vuông góc với AB).
(hai góc so le trong).
Lại có: (do ∆ABD = ∆BAC).
Do đó, , hay .
Suy ra tam giác AMC cân tại đỉnh M.
Khi đó MA = MC.
Mà MB = MC (do M là trung điểm của BC).
Nên MA = MB = MC.
Do đó, tam giác AMB cân tại đỉnh M.
Bài 4.45 trang 69 Toán 7 Tập 1: Cho tam giác ABC là tam giác cân đỉnh A. Chứng minh rằng:
a) Hai đường trung tuyến BM, CN bằng nhau (H.4.50a).
b) Hai đường phân giác BE, CF bằng nhau (H.4.50b).
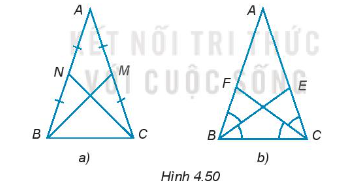
Hướng dẫn giải
a) Do BM và CN là đường trung tuyến của tam giác ABC nên M và N lần lượt là trung điểm của AC và AB.
Khi đó, .
Mà AB = AC (do tam giác ABC cân tại đỉnh A).
Do đó, AM = MC = AN = NB.
Xét tam giác ABM và tam giác ACN có:
AB = AC
: góc chung
AM = AN
Do đó, ∆ABM = ∆ACN (c – g – c).
Suy ra BM = CN (đpcm).
b) Do BE là đường phân giác của góc ABC nên .
Và CF là đường phân giác của góc ACB nên .
Lại có (do tam giác ABC cân tại đỉnh A).
Do đó, .
Xét tam giác ABE và tam giác ACF có:
: góc chung
AB = AC
Do đó, ∆ABE = ∆ACF (g – c – g)
Suy ra, BE = CF (đpcm).
Bài 4.46 trang 69 Toán 7 Tập 1: Cho các điểm A, B, C, D, E như Hình 4.51. Chứng minh rằng:
a) ∆AEB và ∆DEC là các tam giác cân đỉnh E.
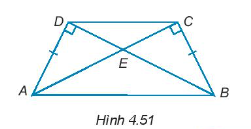
Hướng dẫn giải
a) Xét tam giác vuông ADB và tam giác vuông BCA có:
AB: cạnh huyền chung
AD = CB (gt)
Do đó, ∆ADB = ∆BCA (cạnh huyền – cạnh góc vuông).
Suy ra .
Khi đó tam giác EAB cân tại đỉnh E.
Xét tam giác vuông ADE và tam giác vuông BCE có:
AD = CB (gt)
EA = EB (∆EAB cân tại đỉnh E)
Do đó, ∆ADE = ∆BCE (cạnh huyền – cạnh góc vuông).
Suy ra ED = EC.
Do đó, tam giác EDC cân tại đỉnh E.
b) Theo định lí tổng 3 góc trong tam giác EAB, ta có:
Mà (chứng minh trên)
Suy ra . (1)
Theo định lí tổng 3 góc trong tam giác EDC, ta có:
Mà (∆ECD cân tại đỉnh E).
Suy ra . (2)
Ta lại có: (hai góc đối đỉnh). (3)
Từ (1), (2) và (3) suy ra , hay .
Mà hai góc này ở vị trí so le trong.
Vậy AB // DC.
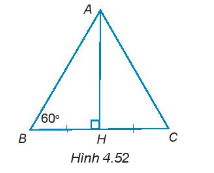
Hướng dẫn giải
+ Xét tam giác vuông ABH và tam giác vuông ACH có:
AH: cạnh chung
HB = HC (gt)
Do đó, ∆ABH = ∆ACH (hai cạnh góc vuông).
Suy ra AB = AC. (1)
Do đó, tam giác ABC cân tại đỉnh A.
⇒ .
Ta có: (định lí tổng ba góc trong tam giác).
Suy ra .
Khi đó , do đó tam giác ABC cân tại đỉnh C nên AC = BC. (2)
Từ (1) và (2) suy ra AB = AC = BC.
Do đó, ∆ABC đều.
+ Vì H thuộc BC và điểm H nằm giữa điểm B và điểm C, hơn nữa HB = HC, do đó H là trung điểm của BC.
Suy ra .
Mà BC = AB (chứng minh trên).
Vậy BH = .
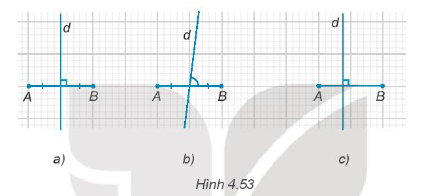
Hướng dẫn giải
Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.
Do đó, trong các Hình 4.53, chỉ có đường thẳng d trong Hình 4.53a là đường trung trực của đoạn thẳng.
a) AB = AC.
b) Tam giác ABC đều.
c) .
d) Tam giác ABC cân tại đỉnh A.
Hướng dẫn giải
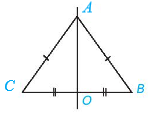
Điểm A thuộc đường trung trực của BC nên AB = AC (điểm thuộc đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó).
Do đó, ∆ABC cân tại đỉnh A.
Suy ra .
Vậy các câu a), c), d) đúng.
Câu b) chưa đúng vì ta chưa đủ dữ kiện để tam giác ABC đều, do ta chỉ có AB = AC, và độ dài đoạn thẳng BC bất kì.
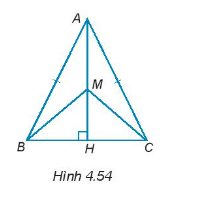
Hướng dẫn giải
Xét tam giác vuông ABH và tam giác vuông ACH có:
AB = AC (∆ABC cân tại đỉnh A)
AH: cạnh chung
Do đó, ∆ABH = ∆ACH (cạnh huyền – cạnh góc vuông).
Suy ra , hay .
Xét tam giác ABM và ACM có:
AB = AC (∆ABC cân tại đỉnh A)
AM: cạnh chung
Do đó, ∆ABM = ∆ACM (c – g – c).
Suy ra .
Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 15: Các trường hợp bằng nhau của tam giác vuông
Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng
Bài 17: Thu thập và phân loại dữ liệu
Bài 18: Biểu đồ hình quạt tròn
1. Tam giác cân và tính chất
• Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau.
Ví dụ: Trong hình dưới đây, có cạnh AB = AC được gọi là tam giác cân tại đỉnh A, hai cạnh AB và AC là hai cạnh bên, BC là cạnh đáy, và là hai góc ở đáy, là góc ở đỉnh.
• Tính chất:
+ Trong tam giác cân, hai góc ở đáy bằng nhau.
+ Tam giác có hai góc ở đáy bằng nhau thì tam giác đó là tam giác cân.
Ví dụ: Tam giác ABC cân tại A thì =. Ngược lại, tam giác ABC có =thì tam giác ABC cân tại A.
Chú ý:
• Tam giác đều là tam giác có ba cạnh bằng nhau. Khi đó ba góc cũng bằng nhau và bằng 60°.
Ví dụ: Tam giác ABC có AB = AC = BC thì tam giác ABC được gọi là tam giác đều. Tam giác ABC đều có = == 60°.
• Một tam giác có ba cạnh hoặc ba góc bằng nhau thì tam giác ấy là tam giác đều.
• Tam giác cân có 1 góc bằng 60° thì tam giác ấy là tam giác đều.
2. Đường trung trực của một đoạn thẳng
• Định nghĩa: Đường thẳng vuông góc với đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.
Ví dụ: Đường thẳng d vuông góc với đoạn AB tại M và M là trung điểm của AB. Khi đó d được gọi là đường trung trực của đoạn thẳng AB.
• Đường trung trực của đoạn thẳng cũng là trục đối xứng của đoạn thẳng đó.
• Tính chất: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Ví dụ: Đường thẳng d là đường trung trực của đoạn thẳng AB và D ∈ d.
Khi đó DA = DB.
• Đường trung trực của đoạn thẳng là tập hợp tất cả các điểm cách đều hai mút của đoạn thẳng đó.
Chú ý:
• Cách vẽ đường trung trực của đoạn thẳng bằng compa và thước thẳng.
Chẳng hạn: Vẽ đường thẳng d là đường trung trực của đoạn thẳng AB như sau:
+ Vẽ đoạn thẳng AB;
+ Lấy A làm tâm, vẽ cung tròn (bán kính lớn hơn ). Sau đó lấy B làm tâm, vẽ cung tròn cùng bán kính sao cho hai cung này cắt nhau tại hai điểm M và N;
+ Dùng thước thẳng vẽ đường thẳng đi qua M và N. Đường thẳng đó là đường trung trực của đoạn thẳng AB.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
