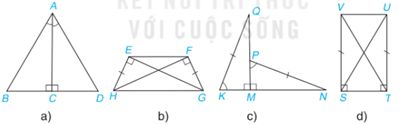
Bài 4.20 trang 79 Toán lớp 7: Mỗi hình sau có các cặp tam giác vuông nào bằng nhau? Vì sao?

Phương pháp giải:

Lời giải:

a)      Xét 2 tam giác vuông ABC và ADC có:

$\widehat{ACB}=\widehat{ACD}(={90}^{\circ })$

AC chung

$\widehat{BAC}=\widehat{DAC}$(gt)

=>$\mathrm{\Delta }ABC=\mathrm{\Delta }ADC$(g.c.g)

b) Xét 2 tam giác vuông HEG và GFH có:

HE=GF(gt)

HG chung

=>$\mathrm{\Delta }HEG=\mathrm{\Delta }GFH$(c.h-c.g.v)

c) Xét 2 tam giác vuông QMK và NMP có:

QK=NP

$\hat{K}=\hat{P}$

=>$\mathrm{\Delta }QMK=\mathrm{\Delta }NMP$(cạnh huyền – góc nhọn)

d) Xét 2 tam giác vuông VST và UTS có:

VS=UT

ST chung

=>$\mathrm{\Delta }VST=\mathrm{\Delta }UTS$(c.g.c)

Bài tập vận dụng:

Bài 1. Mỗi hình sau có các cặp tam giác vuông nào bằng nhau? Vì sao?

Hướng dẫn giải

a) Hai tam giác DEG (vuông tại G) và tam giác DFG (vuông tại G) có:

DG là cạnh chung

$\widehat{EDG}=\widehat{FDG}$

Nên $\Delta DEG=\Delta DFG$ (cạnh góc vuông – góc nhọn kề).

b) Hai tam giác HIK (vuông tại I) và tam giác KJH (vuông tại J) có:

HK là cạnh chung

HI = KJ

Nên $\Delta HIK=\Delta KJH$ (cạnh huyền – cạnh góc vuông).

c) Hai tam giác MLO (vuông tại L) và tam giác ONM (vuông tại N) có:

MO là cạnh chung

$\widehat{LOM}=\widehat{NMO}$

Nên $\Delta MLO=\Delta ONM$ (cạnh huyền –góc nhọn).

d) Hai tam giác SRP (vuông tại R) và tam giác QPR (vuông tại P) có:

RP là cạnh chung

SR = QP

Nên $\Delta SRP=\Delta QPR$ (hai cạnh góc vuông).

Bài 2. Cho hình chữ nhật ABCD, M là trung điểm của cạnh CD. Chứng minh rằng $\Delta ADM=\Delta BCM$.

Hướng dẫn giải

ABCD là hình chữ nhật ⇒ AD = BC và $\widehat{ADM}=\widehat{BCM}=90°$

Xét tam giác ADM (vuông tại D) và tam giác BCM (vuông tại C) có:

AD = BC (chứng minh trên)

DM = CM (theo giả thiết)

⇒ $\Delta ADM=\Delta BCM$ (hai cạnh góc vuông)

Bài 3. Cho hình vẽ dưới đây, biết AB vuông góc với BC, AD vuông góc với CD và cạnh AB = AD. Chứng minh rằng:

a) $\Delta BAC=\Delta DAC$;

b) AC vuông góc với BD.

Hướng dẫn giải

a) Xét tam giác BAC (vuông tại B) và tam giác DAC (vuông tại D) có:

AC là cạnh chung

AB = AD (theo giả thiết)

⇒$\Delta BAC=\Delta DAC$ (cạnh huyền – cạnh góc vuông)

b) Gọi H là giao điểm của AC và BD.

Vì $\Delta BAC=\Delta DAC$ (theo câu a) ⇒ $\widehat{BAC}=\widehat{DAC}$ (hai góc tương ứng) hay $\widehat{BAH}=\widehat{DAH}$

Xét tam giác BAH và tam giác DAH có:

AB = AD (theo giả thiết)

$\widehat{BAH}=\widehat{DAH}$ (chứng minh trên)

AH là cạnh chung

⇒$\Delta BAH=\Delta DAH$ (c.g.c)

⇒$\widehat{AHB}=\widehat{AHD}$ (hai góc tương ứng)

Mà $\widehat{AHB}+\widehat{AHD}=180°$(hai góc kề bù)

Nên $\widehat{AHB}=\widehat{AHD}=90°$

⇒AC ⊥ BD (đpcm).