Tailieumoi.vn xin giới thiệu 3 trường hợp bằng nhau của tam giác và bài tập vận dụng được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm ý thuyết Tam giác bằng nhau. Ngoài ra, bài viết còn gồm bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán. Mời các bạn đón xem:

3 trường hợp bằng nhau của tam giác và bài tập vận dụng

A. Lý thuyết Tam giác bằng nhau

Định nghĩa hai tam giác bằng nhau: Hai tam giác bằng nhau là hai tam giác có csc cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.

Cho tam giác ABC và tam giác A’B’C’.

$\Delta ABC=\Delta A\text{'}B\text{'}C\text{'}$ khi

$\left\{\begin{array}{l}\widehat{A}=\widehat{A\text{'}};\widehat{B}=\widehat{B\text{'}};\widehat{C}=\widehat{C\text{'}}\\ AB=A\text{'}B\text{'};AC=A\text{'}C\text{'};BC=B\text{'}C\text{'}\end{array}\right.$

1. Trường hợp bằng nhau thứ nhất (c – c – c)

Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.

Xét tam giác ABC và tam giác A’B’C’

$\left.\begin{array}{l}AB=A\text{'}B\text{'}\\ AC=A\text{'}C\text{'}\\ BC=B\text{'}C\text{'}\end{array}\right\}\Rightarrow \Delta ABC=\Delta A\text{'}B\text{'}C\text{'}$ (c – c – c)

2. Trường hợp bằng nhau thứ hai (c – g – c)

Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.

Xét tam giác ABC và tam giác A’B’C’ có:

$\left.\begin{array}{l}AB=A\text{'}B\text{'}\\ \widehat{B}=\widehat{B\text{'}}\\ BC=B\text{'}C\text{'}\end{array}\right\}\Rightarrow \Delta ABC=\Delta A\text{'}B\text{'}C\text{'}$ (c – g – c)

3. Trường hợp bằng nhau thứ ba (g – c – g)

Nếu một cạnh và hai góc kề cạnh của tam giác này bằng một cạnh và hai góc kề cạnh của tam giác kia thì hai tam giác đó bằng nhau.

Xét tam giác ABC và tam giác A’B’C’ ta có:

$\left.\begin{array}{l}\widehat{C}=\widehat{C\text{'}}\\ \widehat{B}=\widehat{B\text{'}}\\ BC=B\text{'}C\text{'}\end{array}\right\}\Rightarrow \Delta ABC=\Delta A\text{'}B\text{'}C\text{'}$ (g – c – g)

4. Các trường hợp bằng nhau của tam giác vuông 

• Hai cạnh góc vuông

Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau (cạnh – góc – cạnh )

• Cạnh góc vuông và góc nhọn kề cạnh đó

Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc )

• Cạnh huyền – góc nhọn

Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau ( góc – cạnh – góc)

• Cạnh huyền – cạnh góc vuông

Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

5. Ứng dụng các trường hợp bằng nhau của tam giác

Chúng ta thường vận dụng các trường hợp bằng nhau của tam giác để:

- Chứng minh: hai tam giác bằng nhau, hai đoạn thẳng bằng nhau, hai góc bằng nhau; hai đường thẳng vuông góc; hai đường thẳng song song; ba điểm thẳng hàng; ...

- Tính: các độ dài đoạn thẳng; tính số đo góc; tính chu vi; diện tích; ...

- So sánh: các độ dài đoạn thẳng; so sánh các góc; ...

B. Các dạng bài tập Tam giác bằng nhau

1. Tìm và chứng minh hai tam giác bằng nhau theo trường hợp cạnh – cạnh – cạnh từ đó chứng minh tính chất khác

Phương pháp giải

- Để chứng minh hai tam giác bằng nhau theo trường hợp cạnh – cạnh – cạnh ta làm theo các bước:

+ Xét hai tam giác;

+ Kiểm tra ba cặp cạnh tương ứng bằng nhau;

+ Kết luận hai tam giác bằng nhau (viết đúng thứ tự các đỉnh của hai tam giác).

- Sử dụng trường hợp bằng nhau cạnh – cạnh – cạnh để chứng minh các góc bằng nhau, tính số đo góc ta làm theo các bước:

+ Xác định hai tam giác có các góc cần chứng minh bằng nhau hoặc cần tính số đo;

+ Chứng minh hai tam giác bằng nhau theo trường hợp cạnh – cạnh – cạnh;

+ Suy ra hai góc tương ứng bằng nhau hoặc số đo góc cần tính.

Ngoài ra kết hợp với các tính chất đã học về tia phân giác, đường thẳng song song, tổng ba góc trong một tam giác,…để suy ra những khẳng định đúng.

Ví dụ. Cho $\widehat{\mathrm{xOy}},$ trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OC = OD. Vẽ các cung tròn tâm C và D có cùng bán kính sao cho chúng cắt nhau ở điểm E nằm trong góc xOy. Chứng minh OE là tia phân giác của góc xOy.

Hướng dẫn giải

Chứng minh (Hình vẽ dưới đây):

Vì các cung tròn tâm C và tâm D có cùng bán kính cắt nhau ở điểm E nằm trong góc xOy (giả thiết) nên ta có CE = DE

Xét tam giác OCE và tam giác ODE có:

OC = OD (giả thiết),

CE = DE (chứng minh trên),

OE là cạnh chung

Suy ra ∆OCE = ∆ODE (c.c.c)

Do đó $\widehat{\mathrm{COE}}=\widehat{\mathrm{DOE}}$ (hai góc tương ứng)

Nên tia OE là tia phân giác của góc xOy.

Vậy OE là tia phân giác của góc xOy.

2. Tìm và chứng minh hai tam giác bằng nhau theo trường hợp cạnh – góc – cạnh từ đó chứng minh tính chất khác

Phương pháp giải

- Để chứng minh hai tam giác bằng nhau theo trường hợp cạnh – góc – cạnh ta làm theo các bước:

+ Xét hai tam giác;

+ Kiểm tra hai cặp cạnh bằng nhau và cặp góc xen giữa hai cạnh đó bằng nhau;

+ Kết luận hai tam giác bằng nhau (viết đúng thứ tự các đỉnh của hai tam giác).

- Sử dụng trường hợp bằng nhau cạnh – góc – cạnh để chứng minh các cạnh, các góc bằng nhau, tính độ dài cạnh và số đo góc ta làm theo các bước:

+ Xác định hai tam giác có các cạnh (hoặc góc) cần chứng minh bằng nhau hoặc cạnh cần tính độ dài hay góc cần tính số đo;

+ Chứng minh hai tam giác bằng nhau theo trường hợp cạnh – góc – cạnh;

+ Suy ra các cạnh, các góc tương ứng bằng nhau hoặc độ dài cạnh hay số đo góc cần tính.

Ngoài ra kết hợp với các tính chất đã học về tia phân giác, đường thẳng song song, tổng ba góc trong một tam giác,…để suy ra những khẳng định đúng.

Ví dụ. Cho tam giác nhọn ABC, M là trung điểm của BC. Đường thẳng vuông góc với AB tại B cắt đường thẳng AM tại D. Trên tia MA lấy điểm E sao cho ME = MD. CE cắt AB tại K. Chứng minh:

a) ∆EMC = ∆DMB;

b) ∆AKE vuông tại K.

Hướng dẫn giải

Chứng minh (Hình vẽ dưới đây):

a) Xét tam giác EMC và tam giác DMB có:

ME = MD (giả thiết),

$\widehat{\mathrm{EMC}}=\widehat{\mathrm{DMB}}$ (hai góc đối đỉnh),

MB = MC (do M là trung điểm của BC)

Do đó ∆EMC = ∆DMB (c.g.c)

Vậy ∆EMC = ∆DMB.

b) Vì ∆EMC = ∆DMB (chứng minh câu a)

Suy ra $\widehat{\mathrm{CEM}}=\widehat{\mathrm{BDM}}$ (hai góc tương ứng)

Lại có $\widehat{\mathrm{CEM}}=\widehat{\mathrm{AEK}}$ (hai góc đối đỉnh)

Nên $\widehat{\mathrm{AEK}}=\widehat{\mathrm{BDM}}=\widehat{\mathrm{BDA}}$

Mà $\widehat{\mathrm{BDA}}+\widehat{\mathrm{BAD}}=90°$ (trong tam giác ABD vuông tại B, hai góc nhọn phụ nhau)

Do đó $\widehat{\mathrm{AEK}}+\widehat{\mathrm{KAE}}=90°$

Xét tam giác AKE có: $\widehat{\mathrm{AEK}}+\widehat{\mathrm{KAE}}+\widehat{\mathrm{AKE}}=180°$(tổng ba góc trong một tam giác)

Suy ra $\widehat{\mathrm{AKE}}=180°-\left(\widehat{\mathrm{AEK}}+\widehat{\mathrm{KAE}}\right)$

Hay $\widehat{\mathrm{AKE}}=180°-90°=90°$

Vậy tam giác AKE vuông tại K.

3. Tìm và chứng minh hai tam giác bằng nhau theo trường hợp góc – cạnh – góc. Từ đó chứng minh các cạnh bằng nhau và các góc bằng nhau, tính độ dài cạnh và số đo góc

Phương pháp giải

- Để chứng minh hai tam giác bằng nhau theo trường hợp góc – cạnh – góc ta làm theo các bước:

+ Xét hai tam giác;

+ Kiểm tra một cặp cạnh bằng nhau và hai cặp góc kề cạnh đó bằng nhau;

+ Kết luận hai tam giác bằng nhau (viết đúng thứ tự các đỉnh của hai tam giác).

- Sử dụng trường hợp bằng nhau góc – cạnh – góc để chứng minh các cạnh, các góc bằng nhau, tính số đo góc ta làm theo các bước:

+ Xác định hai tam giác có các cạnh, các góc cần chứng minh bằng nhau hoặc cạnh cần tính độ dài hay góc cần tính số đo;

+ Chứng minh hai tam giác bằng nhau theo trường hợp góc – cạnh – góc;

+ Suy ra hai cạnh tương ứng bằng nhau, hai góc tương ứng bằng nhau hoặc độ dài cạnh hay số đo góc cần tính.

Ngoài ra kết hợp với các tính chất đã học về tia phân giác, đường thẳng song song, tổng ba góc trong một tam giác,…để suy ra những khẳng định đúng.

Ví dụ. Cho tam giác ABC, D là trung điểm của AB. Đường thẳng qua D và song song với BC cắt AC tại E. Đường thẳng qua E và song song với AB cắt BC tại G. Chứng minh:

a) AD = EG;

b) ∆DAE = ∆GEC;

c) G là trung điểm của BC.

Hướng dẫn giải

Chứng minh (hình vẽ dưới đây):

a) Vì DE // BC (giả thiết) nên $\widehat{\mathrm{EDG}}=\widehat{\mathrm{BGD}}$(hai góc so le trong)

Vì EG // AB (giả thiết) nên $\widehat{\mathrm{EDG}}=\widehat{\mathrm{BDG}}$ (hai góc so le trong)

Xét ∆EGD và ∆BDG có:

$\widehat{\mathrm{EDG}}=\widehat{\mathrm{BGD}}$ (chứng minh trên),

DG là cạnh chung,

$\widehat{\mathrm{EGD}}=\widehat{\mathrm{BDG}}$ (chứng minh trên)

Do đó ∆EGD = ∆BDG (g.c.g)

Suy ra EG = BD (hai cạnh tương ứng)

Mà AD = BD (do D là trung điểm của AB)

Do đó AD = EG.

b) Vì DE // BC (giả thiết) nên $\widehat{\mathrm{ADE}}=\widehat{\mathrm{DBG}}$ (hai góc đồng vị)

Vì EG // AB (giả thiết) nên $\widehat{\mathrm{DAE}}=\widehat{\mathrm{GEC}}$ và $\widehat{\mathrm{DBG}}=\widehat{\mathrm{EGC}}$ (các cặp góc đồng vị)

Do đó $\widehat{\mathrm{ADE}}=\widehat{\mathrm{DBG}}=\widehat{\mathrm{EGC}}$

Xét ∆ADE và ∆EGC có:

$\widehat{\mathrm{DAE}}=\widehat{\mathrm{GEC}}$ (chứng minh trên),

AD = EG (chứng minh câu a),

$\widehat{\mathrm{ADE}}=\widehat{\mathrm{EGC}}$(chứng minh trên),

Do đó ∆ADE = ∆EGC (g.c.g)

Vậy ∆ADE = ∆EGC.

c) Từ ∆ADE = ∆EGC (chứng minh câu b) nên DE = GC (hai cạnh tương ứng)

Mà ∆EGD = ∆BDG (chứng minh câu a) nên DE = GB (hai cạnh tương ứng)

Do đó GC = GB (= DE)

Vậy G là trung điểm của BC.

C. Bài tập Tam giác bằng nhau

1. Bài tập trắc nghiệm 

Bài 1: Cho tam giác ABC và tam giác NPM có BC = PM, ∠B = ∠P = 90°.Cần điều kiện gì để tam giác ABC bằng tam giác NPM theo trường hợp cạnh huyền – cạnh góc vuông?

A. BA = PM

B. BA = PN

C. CA = MN

D. ∠A = ∠N

Ta có hai tam giác ABC và tam giác NPM có BC = PM, ∠B = ∠P = 90° mà BC, PM là hai cạnh góc vuông của tam giác ABC và NPM nên để hai tam giác bằng nhau theo trường hợp cạnh huyền – cạnh góc vuông thì ta cần thêm điều kiện CA = MN

Chọn đáp án C.

Bài 2: Cho tam giác ABC và tam giác MNP có ∠A = ∠M = 90°, ∠C = ∠P. Cần điều kiện gì để hai tam giác ABC và tam giác MNP bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề?

A. AC = MP

B. AB = MN

C. BC = NP

D. AC = MN

Ta có: ∠C = ∠P mà góc C và góc P là hai góc nhọn kề của tam giác ABC và tam giác MNP

Do đó để tam giác ABC và tam giác MNP bằng nhau theo trường hợp cạnh hóc vuông – góc nhọn kề thì cần thêm điều kiện AC = MP Chọn đáp án A.

Bài 3: Cho tam giác ABC và tam giác DEF có: ∠B = ∠E = 90°, AC = DF, ∠A = ∠F. Phát biểu nào sau đây đúng?

A. ΔABC = ΔFED

B. ΔABC = ΔFDE

C. ΔBAC = ΔFED

D. ΔABC = ΔDEF

Xét tam giác ABC và tam giác FED có:

==, AC = DF, =Suy ra ΔABC = ΔFED

Chọn đáp án A.

Bài 4: Cho tam giác ABC và tam giác KHI có: ∠A = ∠K = 90°, AB = KH, BC = HI. Phát biểu nào sau đây đúng?

A. ΔABC = ΔKHI

B. ΔABC = ΔHKI

C. ΔABC = ΔKIH

D. ΔACB = ΔKHI

Xét tam giác ABC và tam giác KHI có:

∠A = ∠K = 90°, AB = KH, BC = HI

⇒ ΔABC = ΔKHI

Chọn đáp án A

2. Bài tập tự luận 

Bài 1: Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC. Chứng minh :

a) $\widehat{B}=\widehat{C}$.

b) AM là tia phân giác của $\widehat{BAC}$.

Lời giải:

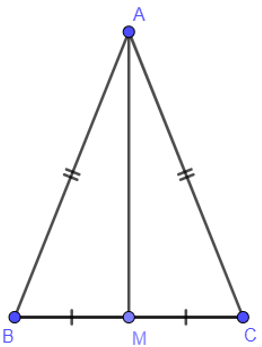
a) Xét tam giác ABM và tam giác ACM có:

AB = AC (giả thuyết)

BM = MC (do M là trung điểm của BC)
AM chung

Do đó $\Delta ABM=\Delta ACM$(c – c – c)

$\Rightarrow \widehat{B}=\widehat{C}$ (hai góc tương ứng).

b) Vì $\Delta ABM=\Delta ACM$$\Rightarrow \widehat{BAM}=\widehat{CAM}$ (hai góc tương ứng)

$\Rightarrow$ AM là phân giác của $\widehat{BAC}$.

Bài 2: Cho tam giác ABC có AB < AC. Phân giác của góc A cắt cạnh BC tại điểm D. Trên cạnh AC lấy E sao cho AE = AB. Chứng minh:

a) $\Delta ABD=\Delta AED$.

b) DA là tia phân giác của góc $\widehat{BDE}$.

c) Chứng minh $\widehat{ABC}>\widehat{ACB}$.

Lời giải:

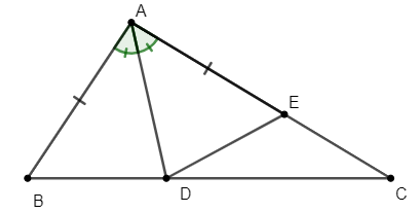
a) Vì AD là tia phân giác $\widehat{A}$$\Rightarrow \widehat{BAD}=\widehat{EAD}$ (tính chất)

Xét tam giác ABD và tam giác AED có:

AB = AE (giả thuyết)

$\widehat{BAD}=\widehat{EAD}$ (chứng minh trên)

AD chung

Do đó $\Delta ABD=\Delta AED$(c – g – c)

b) Vì $\Delta ABD=\Delta AED$$\Rightarrow \widehat{ADB}=\widehat{ADE}$ (hai góc tương ứng)

$\Rightarrow$DA là phân giác $\widehat{BDE}$.

c) Vì $\Delta ABD=\Delta AED$ nên $\widehat{ABD}=\widehat{AED}$ (hai góc tương ứng) hay $\widehat{ABC}=\widehat{AED}$ (1)

Xét tam giác DCE có $\widehat{AED}$ là góc ngoài tại đỉnh E của tam giác

$\Rightarrow \widehat{AED}>\widehat{ACB}$ (tính chất góc ngoài của tam giác)  (2)

Từ (1) và (2)

$\Rightarrow \widehat{ABC}>\widehat{ACB}$ (điều phải chứng minh).

Bài 3: Cho tam giác ABC. Trên tia đối của tia AB lấy điểm M sao cho AM = AB. Qua M kẻ đường thẳng d song song với BC, đường thẳng d cắt CA tại N. Chứng minh:

a) $\Delta ABC=\Delta AMN$;

b) A là trung điểm của NC.

Lời giải:

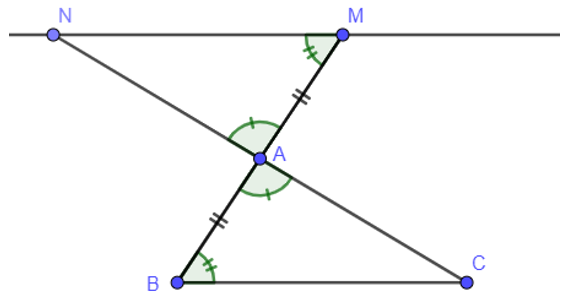
a) Vì đường thẳng d đi qua M song song với BC cắt AC tại N nên MN // BC.

$\Rightarrow \widehat{NMA}=\widehat{ABC}$ (hai góc so le trong)

Xét tam giác AMN và tam giác ABC có:

$\widehat{NMA}=\widehat{ABC}$ (chứng minh trên)

AM = AB (giả thuyết)

$\widehat{BAC}=\widehat{MAN}$ (hai góc đối đỉnh)

Do đó: (g – c – g).

b) Vì $\Delta ABC=\Delta AMN$$\Rightarrow AC=AN$ (hai cạnh tương ứng)

Mà ba điểm A, N, C thẳng hàng

Nên A là trung điểm của NC.

Bài 4: Cho tam giác ABC. Vẽ cung tròn tâm A bán kính BC, vẽ cung tròn tâm C bán bính BA, chúng cách nhau giữa ở D (D và B nằm khác phía đối với bờ AC). Chứng minh rằng AD // BC

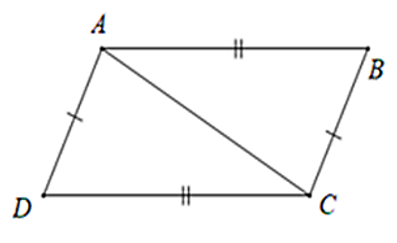
Xét ΔABC và ΔCDA có AC chung

AB = CD (gt)

BC = DA (gt)

Nên ΔABC = ΔCDA (c-c-c)

⇒  (hai góc tương ứng bằng nhau)

mà hai góc ở vị trí so le trong

Do đó AD // BC

Bài 5: Cho đoạn thẳng BC. Gọi A là một điểm nằm trên đường trung trực xy của đoạn thẳng BC và M là giao điểm của xy với BC. Chứng minh AB = AC

Lời giải

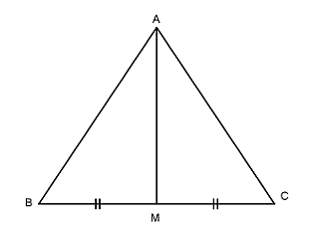
Xét hai tam giác AMB và AMC có:

MB = MC (gt)

 (vì AM ⊥ BC)

AH là cạnh chung

Nên ΔAMB = ΔAMC (c-g-c)

⇒ AB = AC (hai cạnh tương ứng)

Bài 6: Cho đường thẳng AB, trên hai nửa mặt phẳng đối nhau bờ là đoạn thẳng AB vẽ hai tia Ax ⊥ AB; By ⊥ BA. Trên Ax và By lần lượt lấy hai điểm C và D sao cho AC = BD. Gọi O là trung điểm của AB.

a) Chứng mình rằng: ΔAOC = ΔBOD

b) Chứng minh O là trung điểm của CD

Gợi ý đáp án

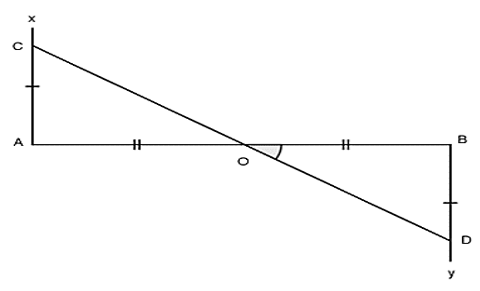
a) Xét ∆AOC và ∆BOD có:

OA = OB (gt)

 

(gt)

 

AC = BD (gt)

 

Suy ra ∆AOC = ∆BOD (c - g - c)

 

b) Vì ∆AOC = ∆BOD (cmt)

 

Mà tia OC và OD là hai tia nằm khác phía đối với AB nên suy ra O, C, D thẳng hàng (hai tia đối của hai góc đối đỉnh hay O nằm giữa CD)

Ta có: O nằm giữa C và D nên OC = OD hay O là trung điểm của CD

Bài 7: Cho ΔABC có . Tia phân giác của góc B cắt AC tại D. Tia phân giác của góc C cắt AB tại E. So sánh độ dài đoạn thằng BD và CE.

Lời giải:

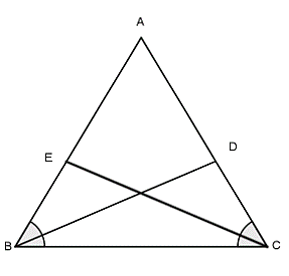
Xét ∆EBC và ∆DCB có:

 (gt)

BC chung

Suy ra ∆EBC = ∆DCB (g - c - g)

Suy ra BD = CE (cặp cạnh tương ứng bằng nhau)

Bài 8: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (H ∈ BC). Chứng minh rằng:

a) HB = HC

b) AH là tia phân giác của góc BAC.

Giải:

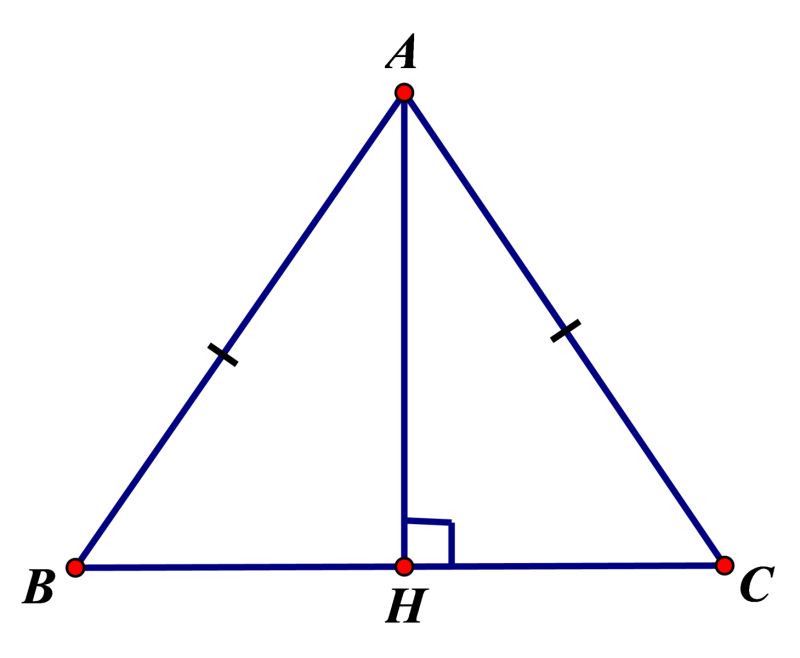
a) ΔABH = ΔACH (cạnh huyền - góc nhọn)

⇒ H B = H C

b) Từ câu a ta có: ˆ BAH = ˆCAH

Bài 9: Cho góc xOy khác góc bẹt. Lấy điểm A thuộc tia Ox, B thuộc tia Oy sao cho OA = OB. Kẻ đường vuông góc với Ox tại A, đường vuông góc với Oy tại B, chúng cắt nhau tại C.

a) Chứng minh: OC là tia phân giác của góc xOy.

b) Gọi I là điểm bất kì thuộc OC. Gọi M, N theo thứ tự là chân đường vuông góc kẻ từ I đến Ox, Oy. Chứng minh: IM = IN.

Giải:

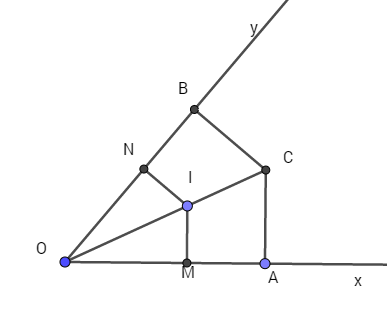
a) ΔOAC = ΔOBC (cạnh huyền - cạnh góc vuông)

⇒ ˆAOC = ˆBOC nên OC là tia phân giác góc xOy.

b) ΔOMI = ΔONI (cạnh huyền - góc nhọn)

⇒ IM = IN

Bài 10: Cho tam giác ABC cân tại A, trên cạnh BC lấy hai điểm D và E sao cho BD = CE <  . Đường thẳng kẻ từ D vuông góc với BC cắt AB tại M, đường thẳng kẻ từ E vuông góc với BC cắt AC tại N. Chứng minh rằng:

a) DM = EN

b) EM = DN

c) Tam giác ADE cân.

Giải:

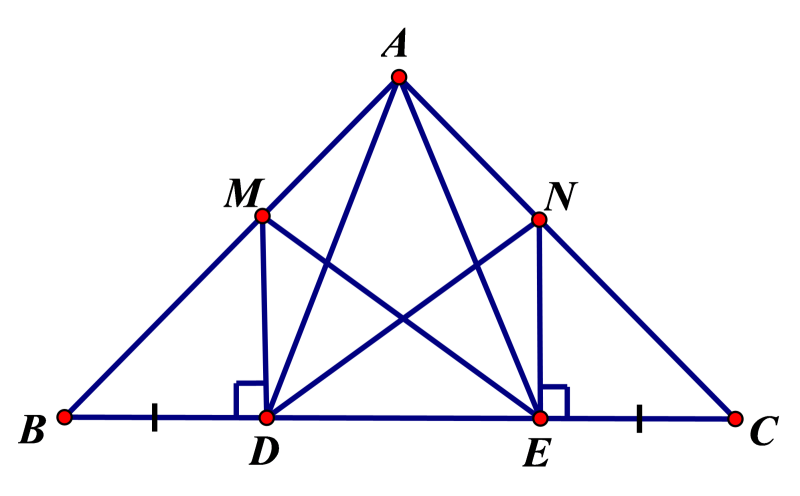
a) ΔMDB = ΔNEC (cạnh góc vuông - góc nhọn) suy ra MD = NE

b) ΔMDE = ΔNED (hai cạnh góc vuông) suy ra ME = ND

c) ΔABD = ΔACE ( cạnh . góc . cạnh ) suy ra AD = AE. Vậy ΔADE cân tại A.

3. Bài tập tự luyện

Bài 1: Cho tam giác ABC; M là trung điểm BC; N là 1 điểm trong tam giác sao cho NB = NC.

Chứng minh: ∆NMB = ∆ NMC.

Bài 2. Cho ABC có AB = AC. Kẻ AE là phân giác của góc BAC (E thuộc BC). Chứng minh rằng: ABE = ACE

Bài 3. Cho tam giác ABC có góc A = 40⁰, AB = AC. Gọi M là trung điểm của BC. Tính các góc của tam giác AMB và tam giác AMC.

Bài 4. Cho tam giác ABC (AB < AC) có AM là phân giác của góc A (M thuộc BC). Trên AC lấy D sao cho AD = AB.

a. Chứng minh BM = MD

b. Gọi K là giao điểm của AB và DM. Chứng minh ∆DAK = ∆BAC

Bài 5. Cho tam giác ABC vuông ở C, có góc A bằng 60⁰, tia phân giác của góc BAC cắt BC ở E. Kẻ EK vuông góc với AB (K thuộc AB), kẻ BD vuông góc với AE (D thuộc AE). Chứng minh:

a. AK = KB

b. AD = BC

Bài 6. Cho tam giác ABC. Qua A kẻ đường thẳng song song với BC, qua C kẻ đường thẳng song song với AB. Hai đường thẳng cắt nhau tại D.

a. Chứng minh ∆ABC =∆ADC

b. Chứng minh ∆ADB = ∆CBD

c. Gọi O là giao điểm của AC và BD. Chứng minh ∆ABO = ∆COD

Bài 7. Cho góc xAy khác góc bẹt. Gọi AD là tia tia phân giác của góc xAy. Qua D kẻ đường thẳng vuông góc với Ay cắt Ay tại C và cắt Ax tại E. Qua D kẻ đường thẳng vuông góc với Ax cắt Ax tại B và cắt Ay tại H. Chứng minh:

a. ∆ABD = ∆ACD

b. ∆DBE = ∆DCH

c. ∆ABH = ∆ACE

Bài 8. Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và D. Trên tia Oy lấy hai điểm C và E sao cho OD = OE và OA = OB.

a. Chứng minh ∆ODC = ∆OBE

b. Gọi A là giao điểm của BE và CD. Chứng minh ∆AOB = ∆AOC

c. Chứng minh BC vuông góc với OA

Bài 9. Cho tam giác ABC có AB = AC. D, E thuộc cạnh BC sao cho BD = DE = EC. Biết AD = AE.

a. Chứng minh góc EAB = góc DAC.

b. Gọi M là trung điểm của BC. Chứng minh AM là phân giác của góc DAE.

c. Giả sử góc DAE = 60⁰. Tính các góc còn lại của tam giác DAE.

Bài 10. Cho ABC có AB = AC. Kẻ AE là phân giác của góc BAC (E thuộc BC). Chứng minh rằng:

a. ∆ABE = ∆ACE

b. AE là đường trung trực của đoạn thẳng BC.

Bài 11. Cho ABC có AB < AC. Kẻ tia phân giác AD của góc BAC (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC. Chứng minh rằng:

a. ∆BDF = ∆EDC.

b. BF = EC.

c. F, D, E thẳng hàng.

d. AD ⊥ FC

Bài 12. Cho góc nhọn xOy. Trên tia Ox, lấy 2 điểm A và C. Trên tia Oy lấy 2 điểm B và D sao cho OA = OB; OC = OD. (A nằm giữa O và C; B nằm giữa O và D).

a. Chứng minh ∆OAD = ∆OBC

b. So sánh 2 góc CAD và CBD.

Bài 13. Cho ΔABC vuông ở A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC.

a. Chứng minh ΔABC = ΔABD

b. Trên tia đối của tia AB, lấy điểm M. Chứng minh ΔMBD = ΔMBC.

Bài 14. Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox, lấy điểm A, trên Oy lấy điểm B sao cho OA = OB. Trên tia Oz, lấy điểm I bất kì. Chứng minh:

a. ΔAOI = ΔBOI.

b. AB ⊥ OI.

Bài 15. Cho ΔABC, M là trung điểm của BC. Trên tia đối của tia MA, lấy điểm E sao cho ME = MA.

a. Chứng minh AC // BE.

b. Gọi I là một điểm trên AC, K là một điểm trên EB sao cho AI = EK. Chứng minh 3 điểm I, M, K thẳng hàng.

Bài 16: Chứng minh hai tam giác bằng nhau thì hai đường cao tương ứng bằng nhau.

Bài 17: Cho góc vuông xAy. Trên tia Ax lấy 2 điểm B và D, trên tia Ay lấy 2 điểm C và E sao cho AB = AC và AD = AE

a. Chứng minh tam giác ACD và tam giác ABE bằng nhau.

b. Chứng minh tam giác BOD và tam giác COE bằng nhau. Với O là giao điểm của DC và BE.

c. Chứng minh AO vuông góc với DE.

Bài 18: Cho góc xOy khác góc bẹt, trên tia Ox lấy 2 điểm A và D trên tia OY lấy 2 điểm C và E sao cho OD = OE và OA = OB

a. Chứng minh tam giác ODC và tam giác OBE bằng nhau.

b. Gọi A là giao điểm của BE và CD. Chứng minh tam giác AOB và tam giác AOC bằng nhau.

c. Chứng minh BC vuông góc với OA.

Bài 19: Cho tam giác ABC có AB = AC. Tia phân giác của góc A cắt BC tại M.

a) Chứng minh: ∆AMB = ∆AMC.

b) Chứng minh M là trung điểm của cạnh BC.

c) K là một điểm bất kì trên đoạn thẳng AM, đường thẳng CK cắt cạnh AB tại I. Vẽ IH vuông góc với BC tại H. Chứng minh góc BAC bằng hai lần góc BIH.

Bài 20. Cho ΔABC và ΔDEF có $\hat{A}=\hat{D},\hat{B}=\hat{E}.$ Để ΔABC = ΔDEF theo trường hợp góc – cạnh – góc thì phải thêm điều kiện nào sau đây:

A. AB = DE;

B. AC = DF;

C. BC = EF;

D. $\widehat{\mathrm{ACB}}=\widehat{\mathrm{DFE}}.$

Bài 21. Cho hình vẽ dưới đây:

Độ dài đoạn thẳng CD bằng:

A. 1 cm;

B. 2 cm;

C. 3 cm;

D. 4 cm.