Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Luyện tập chung trang 74 chi tiết sách Toán 7 Tập 1 Kết nối tri thức với cuộc sống giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:
Giải bài tập Toán lớp Luyện tập chung trang 74
Video bài giảng Toán lớp Luyện tập chung trang 74 - Kết nối tri thức
- Chứng minh hai tam giác bằng nhau theo trường hợp cạnh – góc - cạnh
Từ đó suy ra các cặp cạnh và các cặp góc tương ứng bằng nhau
Lời giải:
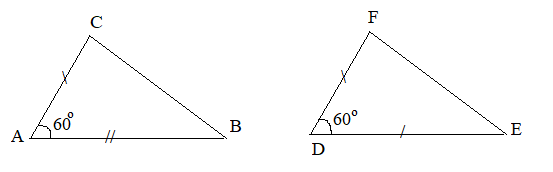
Xét hai tam giác ABC và DEF có:
Suy ra (c.g.c)
Do đó:
Bài 4.17 trang 74 Toán lớp 7: Cho hai tam giác ABC và DEF thoả mãn ,Tính độ dài cạnh DF.
Phương pháp giải:
Lời giải:
Xét hai tam giác ABC và DEF có:
(g.c.g)
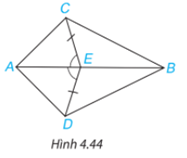
Bài 4.18 trang 74 Toán lớp 7: Cho Hình 4.44, biết và . Chứng minh rằng:
Phương pháp giải:
Lời giải:
a)Xét hai tam giác AEC và AED có
AE chung
(c.g.c)
b)
Do nên và AC=AD.
Xét tam giác ABC và tam giác ABD có:
AB chung
AC=AD
(c.g.c)
a) Chứng minh rằng .
b) Lấy điểm trên tia đối của tia CO. Chứng minh rằng .
Phương pháp giải:
a) Chứng minh hai tam giác bằng nhau theo trường hợp góc – cạnh – góc.
b) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh – góc - cạnh.
Lời giải:
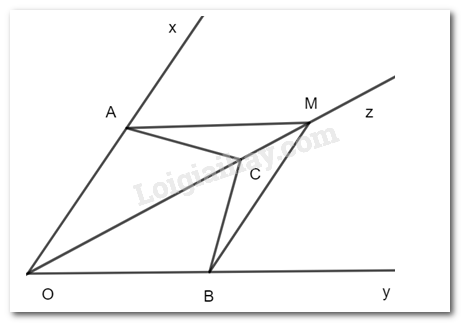
a)
Xét hai tam giác OAC và OBC có:
(Oz là phân giác góc xOy)
OC chung
(g.c.g)
b) Do nên AC=BC ( 2 cạnh tương ứng)
Vì và kề bù
và kề bù
Mà nên
Xét hai tam giác MAC và MBC có:
AC=BC
CM chung
(c.g.c)
Xem thêm các bài giải SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác
Bài 15: Các trường hợp bằng nhau của tam giác vuông
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
