Với giải HĐ 3 trang 76 Toán lớp 7 Kết nối tri thức với cuộc sống chi tiết trong Bài 15: Các trường hợp bằng nhau của tam giác vuông giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:
Giải bài tập Toán lớp 7 Bài 15: Các trường hợp bằng nhau của tam giác vuông
HĐ 3 trang 76 Toán lớp 7: Hình 4.47 mô phỏng chiều dài và độ dốc của hai con dốc bởi các đường thẳng BC, B’C’ và các góc B, B’. Khi đó AC, A’C’ mô tả độ cao của hai con dốc.
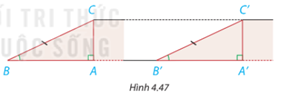
a) Dựa vào trường hợp bằng nhau góc - cạnh - góc của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và A’B’C’ bằng nhau.
b) So sánh độ cao của hai con dốc.
Phương pháp giải:
a) Chứng minh hai tam giác bằng nhau theo trường hợp cạnh huyền – góc nhọn
b) Chứng minh AC=A’C’
Lời giải:
a)Xét hai tam giác vuông ABC và A’B’C’ có:
BC=B’C’
(cạnh huyền – góc nhọn)
b)Do nên AC=A’C’ ( 2 cạnh tương ứng)
Vậy độ cao hai con dốc bằng nhau.
Lý thuyết Ba trường hợp bằng nhau của tam giác vuông
• Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Ví dụ: Trong hình dưới đây, vuông tại A và vuông tại A'có:
AB = A'B'; AC = A'C'. Khi đó = (hai cạnh góc vuông).
• Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Ví dụ: Trong hình dưới đây, vuông tại A và vuông tại A'có:
AC = A'C'; . Khi đó = (cạnh góc vuông – góc nhọn kề).
• Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Ví dụ: Trong hình dưới đây, vuông tại A và vuông tại <A'có:
BC = B'C'; . Khi đó = (cạnh huyền – góc nhọn).
Xem thêm các bài giải Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Xem thêm các bài giải SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 15: Các trường hợp bằng nhau của tam giác vuông
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
