Với giải sách bài tập Toán 7 Bài 15: Các trường hợp bằng nhau của tam giác vuông sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:
Giải SBT Toán lớp 7 Bài 15: Các trường hợp bằng nhau của tam giác vuông
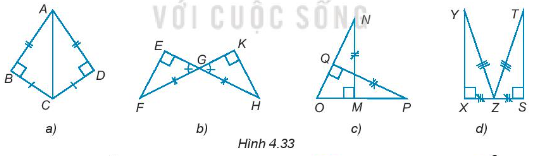
Bài 4.31 trang 64 Toán 7 Tập 1: Trong mỗi hình sau (H.4.33) có các cặp tam giác vuông nào bằng nhau?
Hướng dẫn giải
+) Hình a:
Xét ∆ABC và ∆ADC ta có:
AB = AD (giả thiết)
= = 90° (giả thiết)
BC = CD (giả thiết)
Do đó, ∆ABC = ∆ADC (hai cạnh góc vuông).
+) Hình b
Xét ∆EFG và ∆KHG ta có:
GF = GH (giả thiết)
= = 90° (giả thiết)
= (hai góc đối đỉnh)
Do đó, ∆EFG = KHG (góc nhọn – cạnh huyền)
+) Hình c:
Tam giác OMN vuông tại M nên .
Tam giác OQP vuông tại Q nên .
Do đó, .
Xét ∆OMN và ∆OQP ta có:
MN = PQ (giả thiết)
= = 90o (giả thiết)
(chứng minh trên)
Do đó, ∆OMN = ∆OQP (góc nhọn – cạnh góc vuông).
+) Hình d:
Xét ∆XYZ và ∆STZ ta có:
YZ = TZ (giả thiết)
= = 90° (giả thiết)
XZ = SZ (giả thiết)
Do đó, ∆XYZ = ∆STZ (cạnh huyền – cạnh góc vuông).
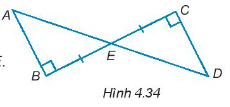
Hướng dẫn giải
Xét ∆ABE và ∆DCE ta có:
∆ABE = ∆CDE (góc nhọn – cạnh góc vuông).
Giải Toán 7 trang 65 Toán 7 Tập 1
Chứng minh rằng:
a) ∆AED = ∆BEC.
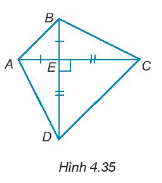
Hướng dẫn giải
a) Xét ∆AED và ∆BEC ta có:
AE = BE (giả thiết)
= = 90° (do AC và DB vuông góc với nhau)
ED = EC (giả thiết)
Do đó, ∆AED = ∆BEC (hai cạnh góc vuông).
b) Ta có: AC = AE + EC; BD = BE + ED. Mà AE = BE; EC = ED nên AC = BD.
Vì ∆AED = ∆BEC nên AD = BC (hai cạnh tương ứng)
Xét ∆ABC và ∆BAD có:
BC = AD (chứng minh trên)
AB chung
AC = BD (chứng minh trên)
Do đó, ∆ABC = ∆BAD (c – c – c).
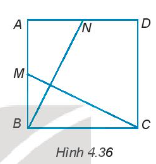
Hướng dẫn giải
Vì ABCD là hình vuông nên AB = BC = CD = DA.
Vì N là trung điểm của AD nên AN = ND = .
Vì M là trung điểm của AB nên AM = MB = .
Mà AB = AD nên AN = BM.
Xét ∆ANB và ∆BMC có:
AN = BM (chứng minh trên)
AB = BC (chứng minh trên)
= = 90° (do ABCD là hình vuông)
Do đó, ∆ANB = ∆BMC (hai cạnh góc vuông)
Suy ra, BN = CM (hai cạnh tương ứng).
Gọi E là giao điểm của BN và CM.
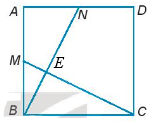
Do ∆ANB = ∆BMC nên .
Từ định lí tổng ba góc trong tam giác BME và tam giác ABN, ta suy ra:
.
Vậy BN vuông góc với CM tại E.
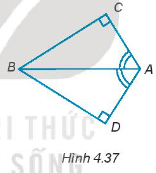
Hướng dẫn giải
Xét ∆ABC và ∆ABD có:
AB chung
= (giả thiết)
= = 90° (giả thiết)
Do đó, ∆ABC = ∆ABD (cạnh huyền – góc nhọn).
Suy ra CB = DB.
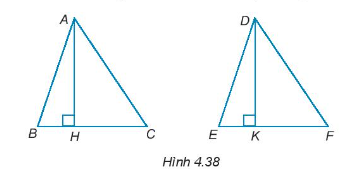
Hướng dẫn giải
Vì ∆ABC = ∆DEF nên
(các góc tương ứng và các cạnh tương ứng bằng nhau).
Vì AH là đường cao của tam giác ABC nên AH vuông góc với BC. Do đó, .
Vì DK là đường cao của tam giác DEF nên DK vuông góc với EF. Do đó, .
Xét ∆ABH và ∆DEK có:
(chứng minh trên)
AB = DE (chứng minh trên)
(chứng minh trên)
Do đó, ∆ABH = ∆DEK (cạnh huyền – góc nhọn).
Suy ra AH = DK.
a) Nếu AB = DE; BC = EF và AH = DK thì ∆ABC = ∆DEF;
b) Nếu AB = DE, AC = DF và AH = DK thì ∆ABC = ∆DEF.
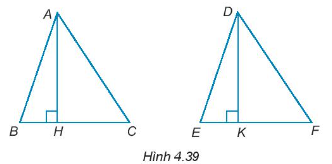
Hướng dẫn giải
a)
Vì AH là đường cao của tam giác ABC nên AH vuông góc với BC. Do đó, .
Vì DK là đường cao của tam giác DEF nên DK vuông góc với EF. Do đó, .
Xét ∆ABH và ∆DEK có:
(chứng minh trên)
AB = DE (giả thiết)
AH = DK (giả thiết)
Do đó, ∆ABH = ∆DEK (cạnh huyền – cạnh góc vuông).
Suy ra, (hai góc tương ứng).
Xét ∆ABC và ∆DEF có:
(chứng minh trên)
AB = DE (giả thiết)
BC = EF (giả thiết)
Do đó, ∆ABC = ∆DEF (c – g – c).
b) Vì AH là đường cao của tam giác ABC nên AH vuông góc với BC. Do đó, .
Vì DK là đường cao của tam giác DEF nên DK vuông góc với EF. Do đó, .
Xét ∆ABH và ∆DEK có:
(chứng minh trên)
AB = DE (giả thiết)
AH = DK (giả thiết)
Do đó, ∆ABH = ∆DEK (cạnh huyền – cạnh góc vuông).
Suy ra, BH = EK.
Xét ∆ACH và ∆DFK có:
(chứng minh trên)
AC = DF (giả thiết)
AH = DK (giả thiết)
Do đó, ∆ACH = ∆DFK (cạnh huyền – cạnh góc vuông).
Suy ra, CH = FK.
Ta có: BC = BH + HC; EF = EK + FK. Mà BH = EK; HC = FK nên BC = EF.
Xét ∆ABC và ∆DEF có:
BC = EF (chứng minh trên)
AC = DF (giả thiết)
AB = DE (giả thiết)
Do đó, ∆ABC = ∆DEF (c – c – c).
a) AC = BD.
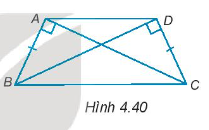
Hướng dẫn giải
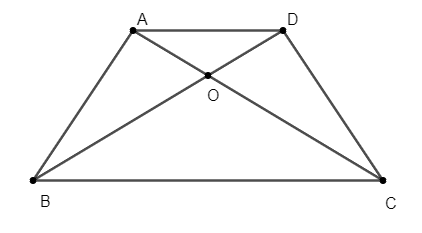
Gọi giao điểm của AC và BD là O.
a) Xét ∆ABC và ∆DCB có:
(giả thiết)
AB = CD (giả thiết)
BC chung
Do đó, ∆ABC = ∆DCB (cạnh huyền – cạnh góc vuông).
Suy ra, AC = BD (hai cạnh tương ứng).
b) Vì ∆ABC = ∆DCB nên (hai góc tương ứng)
Xét tam giác OBC có:
= 180°.
Mà do nên = 180°
Suy ra = 180° –
Do đó, (1)
Xét ∆ABD và ∆DCA có:
AB = CD (giả thiết)
BD = AC (chứng minh trên)
AD chung
Do đó, ∆ABD = ∆DCA (c – c – c).
Suy ra, .
Xét tam giác OAD có:
= 180°.
Mà do nên = 180°
Do đó, (2)
Mà (hai góc đối đỉnh) (3)
Từ (1), (2), (3) suy ra, hay .
Mà hai góc này ở vị trí so le trong nên AD // BC.
a) AF = CE.
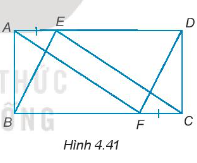
Hướng dẫn giải
a) Vì ABCD là hình chữ nhật nên AD = BC; AB = CD.
Ta có: AD = AE + ED; BC = BF + FC mà FC = AE (gt) và AD = BC nên ED = BF.
Vì ABCD là hình chữ nhật nên .
Xét ∆ABF và ∆CDE có:
AB = CD (chứng minh trên)
BF = ED (chứng minh trên)
(do )
Do đó, ∆ABF = ∆CDE (hai cạnh góc vuông).
Suy ra, AF = CE.
b) Vì ∆ABF = ∆CDE nên (hai góc tương ứng).
Lại có ABCD là hình chữ nhật nên AD // BC nên (hai góc so le trong).
Ta có: ; nên .
Mà hai góc này ở vị trí đồng vị
Nên AF // CE (điều phải chứng minh).
Bài 4.40 trang 66 Toán 7 Tập 1: Cho năm điểm A, B, C, D, E như Hình 4.42, trong đó DA = DC, DB = DE.
a) Chứng minh rằng AB = CE.
b) Cho đường thẳng CE cắt AB tại F. Chứng minh rằng .
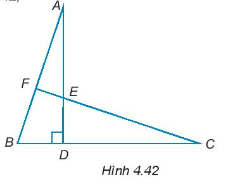
Hướng dẫn giải
a) Xét ∆ABD và ∆CED có:
(giả thiết)
DA = DC (giả thiết)
DB = DE (giả thiết)
Do đó, ∆ABD = ∆CED (hai cạnh góc vuông).
Suy ra, AB = CE (hai cạnh tương ứng).
b) Vì ∆ABD = ∆CED nên (hai góc tương ứng).
Lại có: (do tam giác ABD vuông ở D) nên .
Xét tam giác BFC có:
Mà chính là góc và chính là góc .
Do đó, + = 90°.
Nên + 90° = 180°
Suy ra = 180° – 90° = 90° (điều phải chứng minh).
Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác
Bài 15: Các trường hợp bằng nhau của tam giác vuông
Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng
Bài 17: Thu thập và phân loại dữ liệu
1. Ba trường hợp bằng nhau của tam giác vuông
• Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Ví dụ: Trong hình dưới đây, vuông tại A và vuông tại A'có:
AB = A'B'; AC = A'C'. Khi đó = (hai cạnh góc vuông).
• Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Ví dụ: Trong hình dưới đây, vuông tại A và vuông tại A'có:
AC = A'C'; . Khi đó = (cạnh góc vuông – góc nhọn kề).
• Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Ví dụ: Trong hình dưới đây, vuông tại A và vuông tại <A'có:
BC = B'C'; . Khi đó = (cạnh huyền – góc nhọn).
2. Trường hợp bằng nhau đặc biệt của tam giác vuông
• Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Ví dụ: Trong hình dưới đây, vuông tại A và vuông tại A'có:
BC = B'C'; AC = A'C'. Khi đó = <(cạnh huyền – cạnh góc vuông).
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
