Với giải Bài 9 trang 41 Toán 12 Tập 2 Cánh diều chi tiết trong Bài 4: Ứng dụng hình học của tích phân giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 12. Mời các bạn đón xem:

Giải bài tập Toán 12 Bài 4: Ứng dụng hình học của tích phân

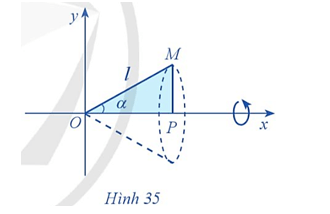
Bài 9 trang 41 Toán 12 Tập 2: Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Giả sử $\widehat{POM}=\alpha ,OM=\mathcal{l}\left(0\le \alpha \le \frac{\pi }{3};\mathcal{l}>0\right)$

Gọi 𝒩 là khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox (Hình 35). Tính thể tích của 𝒩 theo α và ℓ.

Lời giải:

Cách 1:

Tam giác OMP là tam giác vuông tại P nên:

OP = OM ∙ $\cos \widehat{POM}$ = ℓ ∙ cos α;

MP = OM ∙ $\sin \widehat{POM}$ = ℓ ∙ sin α;

Khi đó, điểm M có tọa độ là $\left\{\begin{array}{l}{x}_M=OP=\mathcal{l}\cdot \cos \alpha \\ y_M=MP=\mathcal{l}\cdot \sin \alpha \end{array}\right.$. Suy ra $\left\{\begin{array}{l}\mathcal{l}=\frac{x_M}{\cos \alpha }\\ y_M=\frac{x_M}{\cos \alpha }\cdot \sin \alpha \end{array}\right.$ .

Suy ra y_M = x_M ∙ tan α. Do đó điểm M thuộc đường thẳng y = x ∙ tan α.

Lại có điểm O cũng thuộc đường thẳng trên nên phương trình đường thẳng OM là:

y = x ∙ tan α.

Khi đó, tam giác OPM là hình phẳng giới hạn bởi đồ thị hàm số y = x ∙ tan α, trục Ox và hai đường thẳng x = 0, x = ℓ ∙ cos α. Khối tròn xoay 𝒩 là khối tròn xoay thu được khi quay hình phẳng trên quanh trục Ox.

Thể tích khối tròn xoay này là:

$V=\pi \underset{0}{\overset{\mathcal{l}\cdot \cos \alpha }{\int }}{\left(x\cdot \tan \alpha \right)}^{2}dx=\pi {\tan }^2\alpha \cdot {\left.\frac{x^3}{3}\right|}_0^{\mathcal{l}\cdot \cos \alpha }$

$=\frac{\pi {\tan }^2\alpha }{3}\cdot {\left(\mathcal{l}\cdot \cos \alpha \right)}^3=\frac{\pi {\mathcal{l}}^3}{3}\cdot \frac{{\sin }^2\alpha }{{\cos }^2\alpha }\cdot {\cos }^3\alpha$$=\frac{\pi {\mathcal{l}}^3}{3}\cdot {\sin }^2\alpha \cdot \cos \alpha$.

Cách 2:

Tam giác OMP là tam giác vuông tại P nên:

OP = OM ∙ $\cos \widehat{POM}$ = ℓ ∙ cos α;

MP = OM ∙ $\sin \widehat{POM}$ = ℓ ∙ sin α;

Khi quay tam giác OPM quanh trục Ox ta được khối nón tròn xoay có bán kính đáy là r = MP = ℓ ∙ sin α và chiều cao h = OP = ℓ ∙ cos α.

Thể tích khối nón là:

$V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\pi \cdot {\left(\mathcal{l}\cdot \sin \alpha \right)}^2\cdot \left(\mathcal{l}\cdot \cos \alpha \right)$