Với giải Bài 4.5 trang 67 Toán lớp 7 Kết nối tri thức với cuộc sống chi tiết trong Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:
Giải bài tập Toán lớp 7 Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
Bài 4.5 trang 67 Toán lớp 7: Trong Hình 4.19, hãy chỉ ra hai cặp tam giác bằng nhau.
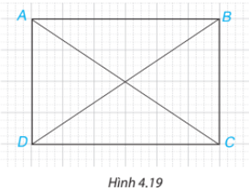
Phương pháp giải:
Lời giải:
Xét hai tam giác ABD và CDB có:
AB = CD (cùng có độ dài bằng 6 ô vuông).
AD = BC (cùng có độ dài bằng 4 ô vuông).
BD chung.
Do đó
Xét hai tam giác ACD và CAB có:
AD = BC (cùng có độ dài bằng 4 ô vuông).
CD = AB (cùng có độ dài bằng 6 ô vuông).
AC chung.
Do đó
Vậy hai cặp tam giác bằng nhau là:
Bài tập vận dụng:
Bài 1. Cho tam giác ABC và DEH trong hình dưới đây.
Xác định trong các khẳng định sau, khẳng định nào đúng?
a) ;
b) ;
c) ;
d) .
Hướng dẫn giải
Hai tam giác ABC và HDE có:
AB = HD
BC = DE
AC = HE
Vậy (c.c.c)
Khi đó A và H (B và D; C và E) là hai đỉnh tương ứng
a)
Các đỉnh tương ứng không viết cùng thứ tự nên khẳng định sai.
b)
Các đỉnh tương ứng được viết cùng thứ tự nên khẳng định đúng.
c)
Đỉnh A và H; đỉnh C và E không được viết cùng thứ tự nên khẳng định sai.
d)
Các đỉnh tương ứng được viết cùng thứ tự nên khẳng định đúng.
Bài 2. Cho hình vẽ dưới đây, biết AD = BC, AC = BD. Chứng minh rằng .
Hướng dẫn giải
Hai tam giác ADB và BCA có:
AD = BC (theo giả thiết)
BD = AC (theo giả thiết)
AB là cạnh chung
Vậy (c.c.c)
Bài 3. Cho hình vẽ dưới đây, biết JG = JL, GK = LK, , .
a) Chứng minh rằng
b) Tính góc GKL.
Hướng dẫn giải
a) Xét hai tam giác JGK và JLK có:
JG = JL (theo giả thiết)
GK = LK (theo giả thiết)
JK là cạnh chung
Vậy (c.c.c)
b) Vì (theo câu a)
⇒ (hai góc tương ứng)
⇒
Xét tam giác JGK có: (tổng 3 góc trong tam giác)
⇒
⇒
Vì (theo câu a)
⇒ (hai góc tương ứng)
⇒
Vậy
Xem thêm các bài giải Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Xem thêm các bài giải SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 12: Tổng các góc trong một tam giác
Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác