Với giải vở thực hành Toán 7 Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong VTH Toán 7. Mời các bạn đón xem:

Giải VTH Toán lớp 7 Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác

Câu 1 trang 58 VTH Toán 7 Tập 1: Khi viết ∆ABC = ∆MNP thì cặp đỉnh nào dưới đây là cặp đỉnh tương ứng?

A. A và N;

B. C và P;

C. B và M;

D. A và P.

Lời giải:

Đáp án đúng là B

Khi ∆ABC = ∆MNP thì ta có các cặp đỉnh tương ứng là:

A và M, B và N, C và P.

Do đó đáp án cần chọn là B

Câu 2 trang 58 VTH Toán 7 Tập 1: Khi viết ∆ABC = ∆MNP thì cặp cạnh nào dưới đây là cặp cạnh tương ứng?

A. AM và BN;

B. AB và NP;

C. AC và MP;

D. BC và MN.

Lời giải:

Đáp án đúng là C

Khi ∆ABC = ∆MNP thì ta có các cặp cạnh tương ứng là:

AB và MN, AC và MP, BC và NP

Do đó đáp án cần chọn là C

Câu 3 trang 58 VTH Toán 7 Tập 1: Biết ∆ABC = ∆DEF và $\hat{E}+\hat{F}=80°$. Câu nào dưới đây đúng?

A. ∆ABC tù;

B. ∆ABC vuông;

C. ∆ABC nhọn;

D. $\hat{A}=80°$.

Lời giải:

Xét ∆DEF, có: $\hat{D}+\hat{E}+\hat{F}=180°$

⇒ $\hat{D}=180°-\left(\hat{E}+\hat{F}\right)=180°-80°=100°$

Vì ∆ABC = ∆DEF nên ta có:

$\hat{A}=\hat{D}=100°$ (hai góc tương ứng)

⇒ $\hat{A}=100°$ là góc tù.

Vậy ∆ABC tù.

Bài 1 (4.4) trang 58 VTH Toán 7 Tập 1: Cho hai tam giác ABC và DEF như Hình 4.18.

Trong các khẳng định sau, khẳng định nào đúng?

(1) $\Delta ABC=\Delta DEF;$

(2) $\Delta ACB=\Delta EDF;$

(3) $\Delta BAC=\Delta DFE;$

(4) $\Delta CAB=\Delta DEF.$

Lời giải:

Các đỉnh tương ứng của hai tam giác ABC và DEF sẽ đối điện các cạnh tương ứng bằng nhau. Do vậy đỉnh A tương ứng với E, đỉnh B tương ứng với đỉnh F, đỉnh C tương ứng với đỉnh D. Do đó các khẳng định 1 và 3 sai; các khẳng định 2 và 4 đúng.

Bài 2 (4.5) trang 59 VTH Toán 7 Tập 1: Trong Hình 4.19, hãy chỉ ra hai cặp tam giác bằng nhau.

Lời giải:

Nhìn hình vẽ ta thấy AD = 4 (bằng 2 lần cạnh ô vuông đơn vị), AB = 6 (bằng ba lần cạnh ô vuông đơn vị). Như vậy ta có:

∆ABD = ∆CDB (c – c – c) (vì AB = CD, AD = BC, BD chung)

∆ADC = ∆CBA (c – c – c) (vì AD = BC, CD = AB, AC chung)

Bài 3 (4.6) trang 59 VTH Toán 7 Tập 1: Cho các điểm A, B, C, D như hình vẽ bên.

a) Chứng minh rằng $\Delta AB\text{D}=\Delta CB\text{D}.$

b) Tính $\widehat{ABC}.$

Lời giải:

a) Hai tam giác ABD và tam giác CBD có:

AB = BC (theo giả thiết).

AD = CD (theo giả thiết)

BD chung.

Do đó ∆ABD = ∆CBD (c – c – c).

b) Vì ∆ABD = ∆CBD nên $\widehat{A\text{D}B}=\widehat{C\text{D}B}=30°$ (2 góc tương ứng).

Do tổng ba góc trong tam giác ABD bằng 180° nên ta có

$\widehat{A\text{D}B}+\widehat{ABD}+\hat{A}=180°$

$\Rightarrow \widehat{ABD}=180°-\widehat{A\text{D}B}-\hat{A}=180°-30°-90°=60°$

Lại vì ∆ABD = ∆CBD, suy ra $\widehat{CBD}=\widehat{ABD}=60°$ (2 góc tương ứng).

Từ đây ta được: $\widehat{ABC}=\widehat{AB\text{D}}+\widehat{CB\text{D}}=60°+60°=120°.$

Bài 4 trang 59 VTH Toán 7 Tập 1: Biết rằng tam giác ABC bằng tam giác MNP, $\widehat{BAC}+\widehat{MNP}=115°$. Hãy tính số đo các góc $\widehat{ACB},\widehat{MPN}$.

Lời giải:

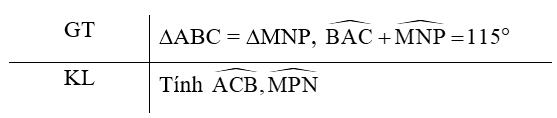
Vì ∆ABC = ∆MNP nên suy ra $\widehat{ABC}=\widehat{MNP}$ (hai góc tương ứng). Do tổng ba góc trong tam giác ABC bằng 180° nên ta có

$\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180°$

⇒$\widehat{ACB}=180°-\widehat{BAC}-\widehat{ABC}$

$=180°-\widehat{BAC}-\widehat{MNP}=180°-115°=65°$

Lại vì ∆ABC = ∆MNP nên ta suy ra $\widehat{MPN}=\widehat{ACB}=65°$ (các góc tương ứng).