Với giải Bài 6 trang 74 Toán 9 Tập 2 Cánh diều chi tiết trong Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác

Bài 6 trang 74 Toán 9 Tập 2: Cho tứ giác ABCD có các tam giác ABC và ADC lần lượt ngoại tiếp các đường tròn (I) và (K) sao cho hai đường tròn này cùng tiếp xúc với đường thẳng AC tại điểm H thuộc đoạn thẳng AC. Giả sử đường tròn (I) tiếp xúc với cạnh AB tại M, đường tròn (K) tiếp xúc với cạnh AD tại N (Hình 17).

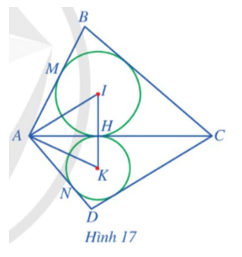
Chứng minh:

a) Ba điểm I, H, K thẳng hàng;

b) AM = AN;

c) $\widehat{IAK}=\frac{1}{2}\widehat{BAD}.$

Lời giải:

a) Vì đường tròn (I) tiếp xúc với đường thẳng AC tại điểm H nên IH ⊥ AC tại H, do đó $\widehat{IHA}=90°.$

Vì đường tròn (K) tiếp xúc với đường thẳng AC tại điểm H nên KH ⊥ AC tại H, do đó $\widehat{KHA}=90°.$

Ta có $\widehat{IHK}=\widehat{IHA}+\widehat{KHA}=90°+90°=180°.$

Suy ra ba điểm I, H, K thẳng hàng.

b) Xét đường tròn (I) có hai tiếp tuyến AB, AC cắt nhau tại A nên điểm A cách đều hai tiếp điểm M và H hay AM = AH (tính chất hai tiếp tuyến cắt nhau).

Xét đường tròn (K) có hai tiếp tuyến AD, AC cắt nhau tại A nên điểm A cách đều hai tiếp điểm N và H hay AN = AH (tính chất hai tiếp tuyến cắt nhau).

Do đó AM = AN.

c) Xét đường tròn (I) có hai tiếp tuyến AB, AC cắt nhau tại A nên AI là đường phân giác của góc BAC, do đó $\widehat{IAH}=\frac{1}{2}\widehat{BAC}.$

Xét đường tròn (K) có hai tiếp tuyến AD, AC cắt nhau tại A nên AK là đường phân giác của góc CAD, do đó $\widehat{HAK}=\frac{1}{2}\widehat{CAD}.$

Ta có: $\widehat{IAK}=\widehat{IAH}+\widehat{HAK}=\frac{1}{2}\widehat{BAC}+\frac{1}{2}\widehat{CAD}=\frac{1}{2}\left(\widehat{BAC}+\widehat{CAD}\right)=\frac{1}{2}\widehat{BAD}.$

Vậy $\widehat{IAK}=\frac{1}{2}\widehat{BAD}.$