Cho tam giác đều MNP có ba đỉnh nằm trên đường tròn (I). Hãy chỉ ra các góc nội

Cho tam giác đều MNP có ba đỉnh nằm trên đường tròn (I). Hãy chỉ ra các góc nội

Trịnh Thị Thu Hiền Ngày: 28-07-2024 Lớp 9

283

Với giải Thực hành 4 trang 93 Toán 9 Tập 1 Chân trời sáng tạo chi tiết trong Bài 3: Góc ở tâm, góc nội tiếp giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 3: Góc ở tâm, góc nội tiếp

Thực hành 4 trang 93 Toán 9 Tập 1: Cho tam giác đều MNP có ba đỉnh nằm trên đường tròn (I). Hãy chỉ ra các góc nội tiếp của đường tròn (I) và tính số đo của các góc nội tiếp đó.

Lời giải:

Thực hành 4 trang 93 Toán 9 Tập 1 Chân trời sáng tạo | Giải Toán 9

Xét đường tròn (I), ta có các góc nội tiếp đường tròn là: $\hat{M N P}, \hat{N P M}, \hat{P M N} .$

Vì ∆MNP là tam giác đều nên $\hat{M N P} = \hat{N P M} = \hat{P M N} = 60 ° .$

Lý Thuyết Góc nội tiếp

Định nghĩa

Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó. Cung nằm bên trong của góc được gọi là cung bị chắn.

Số đo góc nội tiếp

Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.

Ví dụ:

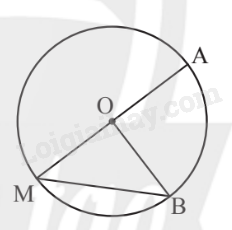
Lý thuyết Góc ở tâm, góc nội tiếp (Chân trời sáng tạo 2024) | Lý thuyết Toán 9 (ảnh 2)

$\hat{A M B}$ là góc nội tiếp chắn $\overset{⌢}{A B}$ trên đường tròn (O) nên $\hat{A M B} = \frac{1}{2}$ sđ $\overset{⌢}{A B}$ .

Chú ý: Trong một đường tròn:

- Các góc nội tiếp bằng nhau chắn các cung bằng nhau.

- Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.

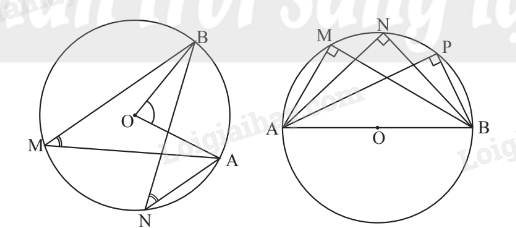
- Góc nội tiếp nhỏ hơn hoặc bằng $90^{o}$ có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.

Góc nội tiếp chắn nửa đường tròn là góc vuông.

Lý thuyết Góc ở tâm, góc nội tiếp (Chân trời sáng tạo 2024) | Lý thuyết Toán 9 (ảnh 3)

Xem thêm lời giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:

Khởi động trang 90 Toán 9 Tập 1: Hình ngôi sao năm cánh trong Hình a được vẽ lại như Hình b. Phần tô màu xanh trên đường tròn từ điểm A đến điểm B được gọi là gì? Làm thế nào để biểu diễn số đo của nó?.......

Khám phá 1 trang 90 Toán 9 Tập 1: Cho hai điểm A, B trên đường tròn (O; R). Nêu nhận xét về đỉnh và cạnh của $\hat{A O B} .$ .......

Thực hành 1 trang 90 Toán 9 Tập 1: Tính số đo góc ở tâm $\hat{E O A}$ và $\hat{A O B}$ trong Hình 3. Biết AC và BE là hai đường kính của đường tròn (O).........

Vận dụng 1 trang 91 Toán 9 Tập 1: Tính số đo góc ở tâm được tạo thành khi kim giờ quay:......

Khám phá 2 trang 91 Toán 9 Tập 1: Vẽ vào vở đường tròn (O) và hai điểm A, B nằm trên (O). Dùng bút chì khác màu tô hai phần của đường tròn được phân chia bởi hai điểm A và B........

Khám phá 3 trang 91 Toán 9 Tập 1: Cho OA và OB là hai bán kính vuông góc với nhau của đường tròn (O), C là điểm trên cung nhỏ AB (Hình 7). Ta coi số đo của một cung nhỏ là số đo của góc ở tâm chắn cung đó........

Thực hành 2 trang 92 Toán 9 Tập 1: Cho đường tròn (O) có hai đường kính AB và CD vuông góc với nhau (Hình 9). Xác định số đo của các cung $\overset{⏜}{A B}, \overset{⏜}{A C}$ và $\overset{⏜}{A D} .$ ........

Vận dụng 2 trang 92 Toán 9 Tập 1: Xác định số đo cung AB trong hình ngôi sao năm cánh (Hình 10)........

Khám phá 4 trang 92 Toán 9 Tập 1: Trên đường tròn (O), vẽ hai cung nhỏ $\overset{⏜}{A B}, \overset{⏜}{B C}$ sao cho $\hat{A O B} = 18 °, \hat{B O C} = 32 °$ và tia OB ở giữa hai tia OA, OC (Hình 11). Tính số đo của các cung $\overset{⏜}{A B}, \overset{⏜}{B C}, \overset{⏜}{A C} .$ .......

Thực hành 3 trang 93 Toán 9 Tập 1: Trên cung AB có số đo 90° của đường tròn (O), lấy điểm M sao cho cung AM có số đo 15°. Tính số đo của cung MB........

Vận dụng 3 trang 93 Toán 9 Tập 1: Bạn Hùng làm một cái diều với thân diều là hình tứ giác SAOB sao cho OS là đường phân giác của $\hat{A O B}$ và $\hat{A S B} = 106 ° .$ Thanh tre màu xanh lá được uốn cong thành cung AB của đường tròn tâm O và SA, SB là hai tiếp tuyến của (O), (Hình 12). Tính số đo của $\overset{⏜}{A B} .$ .......

Khám phá 5 trang 93 Toán 9 Tập 1: Quan sát Hình 13. Hãy cho biết trong các góc $\hat{A P B}, \hat{A O B}, \hat{A M B}, \hat{A Q B},$ góc nào có đỉnh nằm trên đường tròn (O)........

Thực hành 4 trang 93 Toán 9 Tập 1: Cho tam giác đều MNP có ba đỉnh nằm trên đường tròn (I). Hãy chỉ ra các góc nội tiếp của đường tròn (I) và tính số đo của các góc nội tiếp đó.........

Vận dụng 4 trang 93 Toán 9 Tập 1: Cho hai điểm E và F nằm trên đường tròn (O). Có bao nhiêu góc nội tiếp chắn cung EF?........

Khám phá 6 trang 94 Toán 9 Tập 1: Quan sát Hình 15. Ta có góc nội tiếp $\hat{A M B}$ chắn cung AB trên đường tròn (O). Cho biết $\hat{A O B} = 60 ° .$ .......

Thực hành 5 trang 96 Toán 9 Tập 1: Cho ba điểm A, B, C nằm trên đường tròn (O) sao cho $\hat{A O B} = 50 °,$ $\hat{B O C} = 30 °,$ điểm B thuộc cung nhỏ AC. Gọi M, N lần lượt là hai điểm trên hai cung nhỏ $\overset{⏜}{A B}, \overset{⏜}{A C}$ và chia mỗi cung đó thành hai cung bằng nhau. Tìm số đo các góc sau:.......

Vận dụng 5 trang 96 Toán 9 Tập 1: Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn MN (Hình 20). Nếu bóng được đặt ở điểm X thì $\hat{M X N}$ gọi là góc sút từ vị trí X. Hãy so sánh các góc sút $\hat{M X N}, \hat{M Y N}, \hat{M Z N} .$ ........

Bài 1 trang 97 Toán 9 Tập 1: Cho đường tròn (O; 5 cm) và điểm M sao cho OM = 10 cm. Qua M vẽ hai tiếp tuyến với đường tròn tại A và B. Tính số đo góc ở tâm được tạo bởi hai tia OA và OB........

Bài 2 trang 97 Toán 9 Tập 1: Cho tam giác đều ABC. Vẽ nửa đường tròn đường kính BC cắt cạnh AB và AC lần lượt tại D và E. Hãy so sánh các cung $\overset{⏜}{B D}, \overset{⏜}{D E}, \overset{⏜}{E C} .$ .......

Bài 3 trang 97 Toán 9 Tập 1: Dây cung AB chia đường tròn (O) thành hai cung. Cung lớn có số đo bằng ba lần cung nhỏ........

Bài 4 trang 97 Toán 9 Tập 1: Kim giờ và kim phút của đồng hồ tạo thành một góc ở tâm có số đo là bao nhiêu vào những thời điểm sau?......

Bài 5 trang 97 Toán 9 Tập 1: Cho hai đường tròn đồng tâm (O; R) và $(O; \frac{R \sqrt{3}}{2}) .$ Một tiếp tuyến của đường tròn nhỏ cắt đường tròn lớn tại hai điểm A và B. Tính số đo cung AB......

Bài 6 trang 97 Toán 9 Tập 1: Xác định số đo các cung $\overset{⏜}{A B}, \overset{⏜}{B C}, \overset{⏜}{C A}$ trong mỗi hình vẽ sau.......

Bài 7 trang 97 Toán 9 Tập 1: Cho đường tròn (O) có hai đường kính AB, CD vuông góc với nhau. Lấy một điểm M trên cung nhỏ AC rồi vẽ tiếp tuyến với đường tròn (O) tại M. Tiếp tuyến này cắt đường thẳng CD tại S. Chứng minh rằng $\hat{M S D} = 2 \hat{M B A} .$ ......

Xem thêm các bài giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:

Bài 2. Tiếp tuyến của đường tròn

Bài 3. Góc ở tâm, góc nội tiếp

Bài 4. Hình quạt tròn và hình vành khuyên

Bài tập cuối chương 5

Hoạt động 1. Làm giác kế đo góc nâng đơn giản

Hoạt động 2. Vẽ đường tròn bằng phần mềm GeoGebra

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

164

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

141

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

110

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.