Với giải sách bài tập Toán 9 Bài 3: Góc ở tâm, góc nội tiếp sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 3: Góc ở tâm, góc nội tiếp
Bài 1 trang 92 sách bài tập Toán 9 Tập 1: Tìm số đo các cung nhỏ và số đo θ của góc nội tiếp tương ứng trong mỗi hình sau:
Lời giải:
a) Ta có: lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung AL của đường tròn (R).
Do đó
b) Ta có: lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung RM của đường tròn (O).
Do đó
Bài 2 trang 92 sách bài tập Toán 9 Tập 1: Cho đường tròn (O; R) và dây cung Tính số đo của mỗi cung (cung lớn và cung nhỏ).
Lời giải:
Kẻ OH ⊥ MN tại H.
Xét ∆OMN cân tại O (do OM = ON = R) có OH là đường cao nên đồng thời là đường trung tuyến, hay H là trung điểm của MN.
Do đó
Xét ∆HMO vuông tại H, có:
nên
Mà ∆OMN cân tại O nên ta có:
Suy ra số đo cung nhỏ MN là 120°, số đo cung lớn MN là 360° – 120° = 240°.
Bài 3 trang 92 sách bài tập Toán 9 Tập 1: Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M và
a) Tính số đo của góc ở tâm tạo bởi hai bán kính OA, OB.
b) Tính số đo mỗi cung (cung lớn và cung nhỏ).
Lời giải:
a) Vì MA, MB là hai tiếp tuyến của (O) nên OA ⊥ AM; OB ⊥ BM.
Suy ra
Xét tứ giác AOBM, ta có:
Suy ra
Do đó
b) Vì nên số đo cung nhỏ AB là 145° và số đo cung lớn AB là:
360° – 145° = 215°.
Bài 4 trang 93 sách bài tập Toán 9 Tập 1: Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A, B phân biệt. Đường phân giác của cắt các đường tròn (O), (O’) tại các điểm thứ hai theo thứ tự là C và D. So sánh và
Lời giải:
Ta có (vì BC là đường phân giác của (1)
Do B, C thuộc đường tròn (O) nên OB = OC, suy ra ∆OBC cân tại O, do đó (2)
Do B, D thuộc đường tròn (O’) nên O’B = O’D, suy ra ∆O’BD cân tại O’, do đó (3)
Từ (1), (2) và (3) suy ra
Mặt khác, và
Do đó
Bài 5 trang 93 sách bài tập Toán 9 Tập 1: Cho đường tròn (O) đường kính AB và một dây cung AP. Tia AP cắt tiếp tuyến tại B của đường tròn (O) tại T. Chứng minh rằng:
Lời giải:
a) Do AB là đường kính của đường tròn (O), P thuộc đường tròn (O), suy ra
Do đó (1)
Do tia AP cắt tiếp tuyến tại B của đường tròn (O) tại T nên AB ⊥ BT
Do đó (2)
Từ (1), (2) suy ra
Mà (góc nội tiếp và góc ở tâm cùng chắn cung AP) nên hay
b) Do A, P thuộc đường tròn (O) nên AO = OP, do đó ∆AOP cân tại O, suy ra
Mà (cùng phụ với suy ra
Bài 6 trang 93 sách bài tập Toán 9 Tập 1: Cho tam giác nhọn ABC có và có các đỉnh nằm trên đường tròn (O). Các đường cao BH, CK cắt đường tròn (O) tại D, E. Chứng minh ba điểm D, O, E thẳng hàng.
Lời giải:
Do BH, CK là đường cao ∆ABC nên BH ⊥ AC, CK ⊥ AB.
Xét ∆ABH vuông tại H có nên
Mặt khác, (hai góc nội tiếp cùng chắn cung AD) nên (1)
Tương tự, ta có (2)
Từ (1) và (2) suy ra
Mà là góc nội tiếp chắn cung DE nên DE là đường kính của đường tròn (O).
Vậy ba điểm D, O, E thẳng hàng.
Bài 7 trang 93 sách bài tập Toán 9 Tập 1: Vòng ngoài cùng của một guồng nước có dạng đường tròn tâm O, trên đó có đánh dấu 40 điểm chia đường tròn thành 40 cung bằng nhau để gắn các gàu lấy nước. Gọi M, N là hai điểm liên tiếp và P là một điểm khác M, N trong số các điểm nói trên. Tính số đo
Lời giải:
Ta có suy ra số đo góc ở tâm và góc nội tiếp
Xét tam giác MON cân tại O (do OM = ON), ta có:
Lý thuyết Góc ở tâm, góc nội tiếp
1. Góc ở tâm
Định nghĩa
|
Góc ở tâm là góc có đỉnh trùng với tâm đường tròn. |
2. Cung, số đo cung
Cung
|
Mỗi phần đường tròn giới hạn bởi hai điểm A, B trên đường tròn gọi là một cung AB, kí hiệu là . |
Ví dụ:
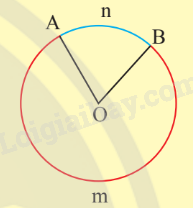
Góc ở tâm chắn cung AnB hay cung AnB bị chắn bởi góc ở tâm .
là cung nhỏ và là cung lớn.
Số đo cung
|
- Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó. - Số đo của cung lớn bằng: - số đo cung nhỏ có chung đầu mút với cung lớn. - Số đo của cung nửa đường tròn bằng . - Số đo của cung AB được kí hiệu là sđ. |
Chú ý:
- Cung nhỏ có số đo nhỏ hơn , cung lớn có số đo lớn hơn . Cung nửa đường tròn có số đo .
- Khi hai mút của cung trùng nhau, ta có cung không với số đo và cung cả đường tròn có số đo .
- Một cung có số đo thường được gọi tắt là cung .
- Trong một đường tròn, hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau.
3. Góc nội tiếp
Định nghĩa
|
Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó. Cung nằm bên trong của góc được gọi là cung bị chắn. |
Số đo góc nội tiếp
|
Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn. |
Ví dụ:
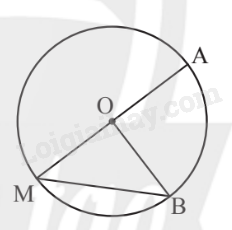
là góc nội tiếp chắn trên đường tròn (O) nên sđ.
Chú ý: Trong một đường tròn:
- Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
- Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
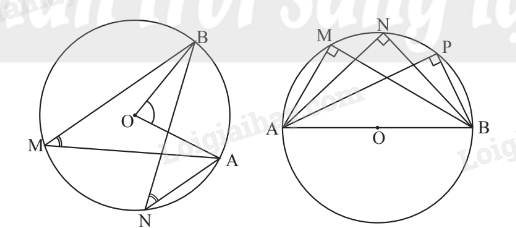
- Góc nội tiếp nhỏ hơn hoặc bằng có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
Góc nội tiếp chắn nửa đường tròn là góc vuông.
Xem thêm các bài giải SBT Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Tiếp tuyến của đường tròn
Bài 3: Góc ở tâm, góc nội tiếp
Bài 4: Hình quạt tròn và hình vành khuyên