Với giải Luyện tập 2 trang 95 Toán 9 Tập 1 Cánh diều chi tiết trong Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn

Luyện tập 2 trang 95 Toán 9 Tập 1: Cho tam giác nhọn ABC. Đường tròn tâm O đường kính BC cắt các cạnh AB và AC lần lượt tại M và N. Chứng minh MN < BC.

Lời giải:

Nối OM, ON.

Xét ∆OMN, ta có: MN < OM + ON (Bất đẳng thức tam giác). (1)

Vì B, M, N, C cùng thuộc đường tròn (O) nên OA = OM = ON = OB.

Ta có: OM + ON = OB + OC.

Lại có BC là đường kính của đường tròn (O) nên BC = OB + OC.

Do đó OM + ON < BC. (2)

Từ (1) và (2) suy ra MN < AB.

Lý thuyết Liên hệ giữa đường kính và dây của đường tròn

Chú ý:

- Đoạn thẳng nối hai điểm phân biệt thuộc đường tròn được gọi là dây (hay dây cung) của đường tròn.

- Dây đi qua tâm là đường kính của đường tròn. Trong các dây của đường tròn, dây lớn nhất là đường kính.

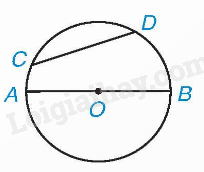
Ví dụ: Cho hai điểm C, D cùng thuộc một đường tròn. Đoạn thẳng CD gọi là dây cung hoặc dây. Đường kính AB  là một dây đi qua tâm.