Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 9 Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn chi tiết sách Toán 9 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:
Giải bài tập Toán 9 Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn
Khởi động trang 93 Toán 9 Tập 1: Mỗi bánh xe đạp ở Hình 1 gợi nên hình ảnh của một đường tròn.
Hai đường tròn đó có điểm chung hay không?
Lời giải:
Hai đường tròn mô tả hai bánh xe đạp không có điểm chung.
Lời giải:
Khi kim phút quay một vòng thì đầu mút của kim phút vạch nên đường tròn.
1. Khái niệm đường tròn
Lời giải:
Một số đồ vật trong thực tiễn gợi nên hình ảnh của đường tròn là bánh xe, biển báo giao thông, bàn ăn hình tròn, gương trang điểm hình tròn, …
2. Liên hệ giữa đường kính và dây của đường tròn
Hoạt động 2 trang 94 Toán 9 Tập 1: Quan sát Hình 5.
a) So sánh MN và OM + ON.
b) So sánh MN và AB.
Lời giải:
a) Xét ∆OMN ta có MN < OM + ON (1) (Bất đẳng thức tam giác).
b) Vì A, M, N, B cùng thuộc đường tròn (O) nên OA = OM = ON = OB.
Ta có: OM + ON = OA + OB.
Lại có AB = OA + OB, do đó OM + ON < AB. (2)
Từ (1) và (2) suy ra MN < AB.
Lời giải:
Nối OM, ON.
Xét ∆OMN, ta có: MN < OM + ON (Bất đẳng thức tam giác). (1)
Vì B, M, N, C cùng thuộc đường tròn (O) nên OA = OM = ON = OB.
Ta có: OM + ON = OB + OC.
Lại có BC là đường kính của đường tròn (O) nên BC = OB + OC.
Do đó OM + ON < BC. (2)
Từ (1) và (2) suy ra MN < AB.
3. Tính đối xứng của đường tròn
Hoạt động 3 trang 95 Toán 9 Tập 1: Cho đường tròn (O; R).
a) Vẽ đường thẳng d đi qua tâm O cắt đường tròn tại A, B. So sánh OA và OB (Hình 7).
b) Giả sử M là một điểm tùy ý trên đường tròn (O; R). Trên tia đối của tia OM, ta lấy điểm N sao cho ON = OM. Điểm N có thuộc đường tròn (O; R) hay không?
Lời giải:
a) Ta thấy A và B cùng thuộc đường tròn (O; R) nên OA = OB = R.
b) Vì M thuộc đường tròn (O; R) nên OM = R.
Mà OM = ON nên OM = ON = R, suy ra N thuộc đường tròn (O; R).
Lời giải:
Nối OM, ON.
Xét ∆OMH (vuông tại H)và ∆ONH (vuông tại H) ta có:
MH = NH (do H là trung điểm của MN);
OH là cạnh chung.
Do đó ∆OMH = ∆ONH (hai cạnh góc vuông).
Suy ra OM = ON (hai cạnh tương ứng).
Mà M thuộc đường tròn (O; R) nên OM = R nên ON = R, do đó N thuộc đường tròn (O; R).
Lời giải:
Để xác định tâm của hình đó ta làm theo ba bước sau:
Bước 1. Gấp đôi tờ giấy sao cho hai mép của tờ giấy trùng khít lên nhau ta được hình nửa đường tròn.
Bước 2. Tiếp tục gấp đôi tờ giấy hình nửa đường tròn đó sao cho mép của tờ giấy trùng khít lên nhau.
Bước 3. Mở tờ giấy ra ta thấy xuất hiện giao của hai đường kính, đó chính là tâm hình tròn cần tìm.
4. Vị trí tương đối của hai đường tròn
Lời giải:
Hai đường tròn cắt nhau thì có 2 điểm chung.
Lời giải:
Ta thấy bán kính của hai đường tròn (O) và (O’) lần lượt là R = 14 cm và r = 5 cm.
Do R – r = 14 – 5 = 9 (cm); R + r = 14 + 5 = 19 (cm)
Và 8 < 9 < 19 nên OO’ < R – r < R + r.
Vậy hai đường tròn (O; 14 cm) và (O’; 5 cm) không cắt nhau.
Lời giải:
Hai đường tròn tiếp xúc nhau thì chúng có 1 điểm chung.
Lời giải:
Ta thấy bán kính của hai đường tròn (O) và (O’) lần lượt là r = 2,5 cm và R = 4,5 cm.
Để hai đường tròn đó tiếp xúc trong thì OO’ = R – r = 4,5 – 2,5 = 2 (cm).
Vậy OO’ = 2 cm thì hai đường tròn đó tiếp xúc trong.
Lời giải:
Hai đường tròn không giao nhau thì chúng không có điểm chung.
Lời giải:
Ta thấy bán kính của hai đường tròn (O) và (O’) lần lượt là R = 11,5 cm và r = 6,5 cm.
Do R – r = 11,5 – 6,5 = 5 (cm) và 4 < 5 nên OO’ < R – r.
Vậy đường tròn (O; 11,5 cm) đựng đường tròn (O’; 6,5 cm).
Bài tập
Lời giải:
Xét đường tròn đường kính AC, có dây cung CD, do đó CD < AC (trong các dây của đường tròn, dây lớn nhất là đường kính).
Xét đường tròn đường kính AB, có dây cung AC, do đó AC < AB (trong các dây của đường tròn, dây lớn nhất là đường kính).
Do đó CD < AC < AB.
Lời giải:
a) Ta có:
⦁ Hai đường tròn (O; R) và (O’; R’) không có điểm chung;
⦁ OO’ > R + R’.
Do đó hai đường tròn (O) và (O’) ở ngoài nhau.
b) Ta có:
⦁ Hai đường tròn (O; R) và (O’; R’) có 1 điểm chung duy nhất;
⦁ OO’ = R + R’.
Do đó hai đường tròn (O) và (O’) tiếp xúc ngoài.
c) Ta có:
⦁ Hai đường tròn (O; R) và (O’; R’) không có điểm chung;
⦁ OO’ < R’ – R.
Do đó đường tròn (O’) đựng đường tròn (O).
d) Ta thấy hai đường tròn (O) và (O’) có 2 điểm chung nên hai đường tròn (O) và (O’) cắt nhau.
a) Vẽ đường tròn tâm O bán kính R = OM.
b) Chứng minh điểm N thuộc đường tròn (O; R).
Lời giải:
a) Hình vẽ:
b) Vì O nằm đường trung trực của đoạn thẳng MN nên OM = ON.
Mà OM = R (câu a) nên ON = R.
Vậy N thuộc đường tròn (O; R).
Bài 4 trang 100 Toán 9 Tập 1: Cho đường tròn (O; R) và dây AB = R. Tính số đo góc AOB.
Lời giải:
Vì AB là dây cung của đường tròn (O; R) nên OA = OB = R.
Mà AB = R nên OA = OB = AB = R.
Xét ∆OAB có OA = OB = AB = R nên ∆OAB là tam giác đều, suy ra
Quan sát Hình 18 và chỉ ra một cặp đường tròn:
a) Cắt nhau;
b) Tiếp xúc ngoài;
c) Tiếp xúc trong;
d) Không giao nhau.
Lời giải:
a) Một cặp đường tròn cắt nhau: Đường tròn màu đỏ và đường tròn màu vàng (khung đồng hồ).
b) Một cặp đường tròn tiếp xúc ngoài: Đường tròn màu xanh lá và đường tròn màu cam.
c) Một cặp đường tròn tiếp xúc trong: Đường tròn màu xanh cổ vịt (mặt đồng hồ) và đường tròn màu vàng (khung đồng hồ).
d) Một cặp đường tròn không giao nhau: Đường tròn màu vàng và đường tròn màu tím (quả lắc).
a) Đường thẳng OM có phải là đường trung trực của đoạn thẳng AB hay không? Vì sao?
b) Tính khoảng cách từ điểm O đến đường thẳng AB, biết R = 5 cm, AB = 8 cm.
Lời giải:
a) Vì AB là dây cung của đường kính (O; R) nên ta có OA = OB = R.
Khi đó, O nằm trên đường trung trực của AB.
Lại có M là trung điểm của AB nên M cũng nằm trên đường trung trực của AB.
Do đó OM là đường trung trực của đoạn thẳng AB.
b) Vì M là trung điểm của AB nên ta có MA = MB = = 4 (cm).
Vì OM là đường trung trực của đoạn thẳng AB nên OM ⊥ AB hay ∆OAM vuông tại M.
Theo định lí Pythagore ta có: OA2 = OM2 + AM2
Suy ra OM2 = OA2 – AM2 = 52 – 42 = 9.
Do đó OM = 3 cm.
Vậy khoảng cách từ điểm O đến đường thẳng AB là 3 cm.
a)
b) AB // A’B’.
Lời giải:
a) Ta có: suy ra
b) Xét ∆OAB có nên AB // A’B’ (theo định lí Thalès đảo).
Xem thêm các bài giải bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:
§1. Đường tròn. Vị trí tương đối của hai đường tròn
§2. Vị trí tương đối của đường thẳng và đường tròn
§5. Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên
Lý thuyết Đường tròn. Vị trí tương đối của hai đường tròn
1. Khái niệm đường tròn
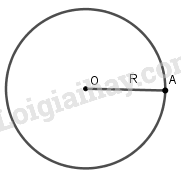
|
Trong mặt phẳng, đường tròn tâm O bán kính R là tập hợp các điểm cách điểm O một khoảng bằng R (R > 0), kí hiệu là (O;R). |
Chú ý:
- Một đường tròn hoàn toàn xác định khi biết tâm và bán kính.
- Khi không quan tâm đến bán kính của đường tròn (O;R), ta cũng có thể kí hiệu đường tròn là (O).
Vị trí tương đối của điểm và đường tròn
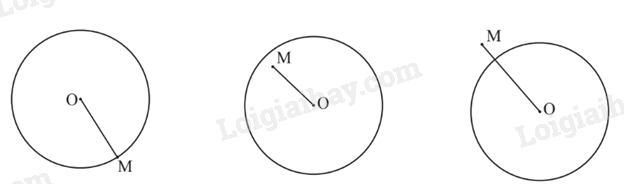
Cho đường tròn (O; R) và điểm M. Khi đó:
- Nếu điểm M thuộc đường tròn (O) (hay ta còn nói điểm M nằm trên đường tròn (O), hoặc đường tròn (O) đi qua điểm M) thì OM = R và ngược lại.
- Nếu điểm M nằm bên trong (hay nằm trong, ở trong) đường tròn (O) thì OM < R và ngược lại.
- Nếu điểm M nằm bên ngoài (hay nằm ngoài, ở ngoài) đường tròn (O) thì OM > R và ngược lại.
2. Liên hệ giữa đường kính và dây của đường tròn
Chú ý:
- Đoạn thẳng nối hai điểm phân biệt thuộc đường tròn được gọi là dây (hay dây cung) của đường tròn.
- Dây đi qua tâm là đường kính của đường tròn. Trong các dây của đường tròn, dây lớn nhất là đường kính.
Ví dụ: Cho hai điểm C, D cùng thuộc một đường tròn. Đoạn thẳng CD gọi là dây cung hoặc dây. Đường kính AB là một dây đi qua tâm.
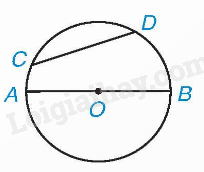
3. Tính đối xứng của đường tròn
Nhận xét: Điểm đối xứng của một điểm tùy ý trên đường tròn qua tâm của đường tròn cũng nằm trên đường tròn đó.
|
Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó. |
Nhận xét: Điểm đối xứng của một điểm tùy ý trên đường tròn qua một đường thẳng đi qua tâm của đường tròn cũng nằm trên đường tròn đó.
|
Đường tròn là hình có trục đối xứng. Mỗi đường thẳng đi qua tâm là một trục đối xứng của đường tròn đó. |
Ví dụ:
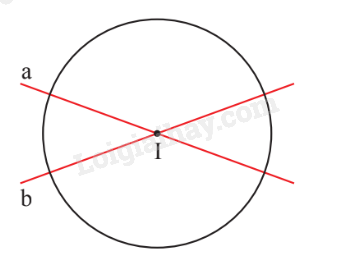
Hình tròn tâm I có:
I là tâm đối xứng;
Đường thẳng a, b là các trục đối xứng của hình tròn (I).
4. Vị trí tương đối của hai đường tròn
Hai đường tròn cắt nhau
|
Hai đường tròn có đúng hai điểm chung gọi là hai đường tròn cắt nhau.
|
Mỗi điểm chung của hai đường tròn cắt nhau được gọi là một giao điểm của hai đường tròn đó.
Nếu hai đường tròn (O;R) và (O’;r) với cắt nhau thì .
Hai đường tròn tiếp xúc nhau
|
Hai đường tròn có đúng một điểm chung gọi là hai đường tròn tiếp xúc nhau (tại điểm chung đó). |
Điểm chung của hai đường tròn tiếp xúc nhau được gọi là tiếp điểm.
Có hai trường hợp về hai đường tròn tiếp xúc nhau:
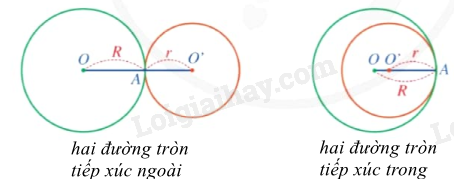
Nếu hai đường tròn (O;R) và (O’;r) tiếp xúc ngoài thì tiếp điểm A nằm giữa O, O’ và . Điều ngược lại cũng đúng.
Với R > r, nếu hai đường tròn (O;R) và (O’;r) tiếp xúc trong thì điểm O’ nằm giữa O, A và . Điều ngược lại cũng đúng.
Hai đường tròn không giao nhau
|
Hai đường tròn không có điểm chung gọi là hai đường tròn không giao nhau. |
Có hai trường hợp về hai đường tròn không giao nhau:
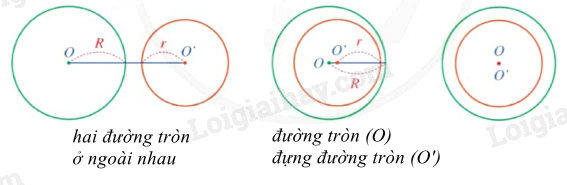
Nếu hai đường tròn (O;R) và (O’;r) ở ngoài nhau thì . Điều ngược lại cũng đúng.
Với R > r, nếu đường tròn (O) đựng đường tròn (O’) thì . Điều ngược lại cũng đúng.
Nhận xét: Ta có thể nhận biết vị trí tương đối của hai đường tròn thông qua hệ thức liên hệ giữa OO’ với R và r được tóm tắt trong bảng sau:
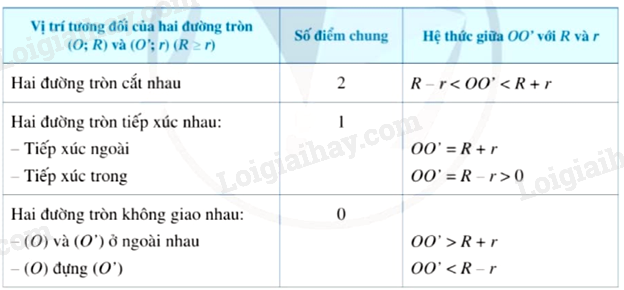
Ví dụ 1: Cho OO’ = 5cm, khi đó hai đường tròn (O;4cm) và (O’;3cm) cắt nhau vì:
4cm – 3cm = 1cm < 5cm < 7cm = 4cm + 3cm.
Ví dụ 2: Cho OO’ = 5cm, khi đó hai đường tròn (O;3cm) và (O’;2cm) tiếp xúc ngoài với nhau vì 5cm = 3cm + 2cm.
Cho OO’ = 3cm, khi đó hai đường tròn (O;8cm) và (O’;5cm) tiếp xúc trong với nhau vì 3cm = 8cm - 5cm.
Ví dụ 3: Cho đường tròn (O;3cm) và (O’;4cm) có thì nên (O;3cm) và (O’;4cm) là hai đường tròn ngoài nhau.