Xét tam giác ABC trong Hình 4.16. Viết các tỉ số lượng giác tang, côtang của góc B và góc C theo b, c

Xét tam giác ABC trong Hình 4.16. Viết các tỉ số lượng giác tang, côtang của góc B và góc C theo b, c

Trịnh Thị Thu Hiền Ngày: 24-07-2024 Lớp 9

206

Với giải HĐ2 trang 75 Toán 9 Tập 1 Kết nối tri thức chi tiết trong Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

HĐ2 trang 75 Toán 9 Tập 1: Xét tam giác ABC trong Hình 4.16.

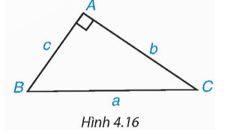
HĐ2 trang 75 Toán 9 Tập 1 | Kết nối tri thức Giải Toán 9

a) Viết các tỉ số lượng giác tang, côtang của góc B và góc C theo b, c.

b) Tính mỗi cạnh góc vuông b và c theo cạnh góc vuông kia và các tỉ số lượng giác trên của góc B và góc C.

Lời giải:

a) Xét ∆ABC vuông tại A, theo định nghĩa tỉ số lượng giác và định lí về tỉ số lượng giác của hai góc phụ nhau, ta có:

$\tan B = \cot C = \frac{A C}{A B} = \frac{b}{c}; \tan C = \cot B = \frac{A B}{A C} = \frac{c}{b} .$

b) Từ $\tan B = \cot C = \frac{A C}{A B} = \frac{b}{c},$ ta có b = c.tanB = c.cotC.

Từ $\tan C = \cot B = \frac{A B}{A C} = \frac{c}{b},$ ta có c = btanC = bcotB.

Lý Thuyết Hệ thức giữa hai cạnh góc vuông

Công thức tính cạnh góc vuông theo cạnh góc vuông kia và tang, côtang của các góc nhọn

Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh góc vuông kia nhân với tang góc đối hoặc côtang góc kề.

Cạnh góc vuông = (cạnh góc vuông còn lại ) × (tan góc đối)

= (cạnh góc vuông còn lại ) × (cot góc kề)

Ví dụ 2:

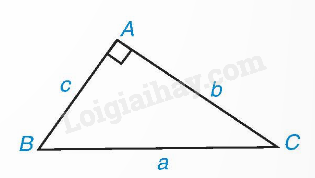
Lý thuyết Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng (Kết nối tri thức 2024) | Lý thuyết Toán 9 (ảnh 2)

Trong tam giác ABC vuông tại A, ta có:

$\begin{array}{l} b = c . \tan B = c . \cot C; \\ c = b . \tan C = b . \cot B . \end{array}$

Xem thêm lời giải bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác:

Mở đầu trang 74 Toán 9 Tập 1: Để đo chiều cao của một toà lâu đài (H.4.11), người ta đặt giác kế thẳng đứng tại điểm M. Quay ống ngắm của giác kế sao cho nhìn thấy đỉnh P’ của toà lâu đài dưới góc nhọn α. Sau đó, đặt giác kế thẳng đứng tại điểm N, NM = 20 m, thì nhìn thấy đỉnh P’ dưới góc nhaọn β (β < α). Biết chiều cao giác kế là 1,6 m, hãy tính chiều cao của toà lâu đài.......

HĐ1 trang 74 Toán 9 Tập 1: Cho tam giác ABC vuông tại A, cạnh huyền a và các cạnh góc vuông b, c (H.4.12).......

Luyện tập 1 trang 75 Toán 9 Tập 1: Một chiếc thang dài 3 m. Cần đặt chân thang cách chân tường một khoảng bằng bao nhiêu mét (làm tròn đến chữ số thập phân thứ hai) để nó tạo được với mặt đất một góc “an toàn” 65° (tức là đảm bảo thang chắc chắn khi sử dụng) (H.4.14)?.....

Luyện tập 1 trang 75 Toán 9 Tập 1: Một khúc sông rộng khoảng 250 m. Một con đò chèo qua sông bị dòng nước đẩy xiên nên phải chèo khoảng 320 m mới sang được bờ bên kia. Hỏi dòng nước đã đẩy con đò đi lệch một góc α bằng bao nhiêu độ (làm tròn đến phút)? (H.4.15).......

HĐ2 trang 75 Toán 9 Tập 1: Xét tam giác ABC trong Hình 4.16......

Luyện tập 2 trang 76 Toán 9 Tập 1: Bóng trên mặt đất của một cây dài 25 m. Tính chiều cao của cây (làm tròn đến dm), biết rằng tia nắng mặt trời tạo với mặt đất góc 40° (H.4.18).......

Luyện tập 3 trang 77 Toán 9 Tập 1: Cho tam giác vuông ABC có cạnh góc vuông AB = 4, cạnh huyền BC = 8. Tính cạnh AC (làm tròn đến chữ số thập phân thứ ba) và các góc B, C (làm tròn đến độ)......

Câu hỏi trang 77 Toán 9 Tập 1: Hãy nêu cách giải tam giác ABC vuông tại A khi biết hai cạnh AB = c, AC = b hoặc AB = c, BC = a và không sử dụng định lí Pythagore (H.4.21).......

Câu hỏi trang 77 Toán 9 Tập 1: Hãy nêu cách giải tam giác ABC vuông tại A khi biết cạnh góc vuông AB (hoặc cạnh huyền BC) và góc B........

Luyện tập 4 trang 77 Toán 9 Tập 1: Giải tam giác ABC vuông tại A, biết BC = 9, $\hat{C} = 53 ° ........$

Vận dụng trang 77 Toán 9 Tập 1: Giải bài toán ở tình huống mở đầu với α = 27° và β = 19°.......

Bài 4.8 trang 78 Toán 9 Tập 1: Giải tam giác ABC vuông tại A có BC = a, AC = b, AB = c, trong các trường hợp:......

Bài 4.9 trang 78 Toán 9 Tập 1: Tính góc nghiêng α của thùng xe chở rác trong Hình 4.22.......

Bài 4.10 trang 78 Toán 9 Tập 1: Tìm góc nghiêng α và chiều rộng AB của mái nhà kho trong Hình 4.23.......

Bài 4.11 trang 78 Toán 9 Tập 1: Tính các góc của hình thoi có hai đường chéo dài $2 \sqrt{3}$ và 2......

Bài 4.12 trang 78 Toán 9 Tập 1: Cho hình thang ABCD (AD // BC) có AD = 16 cm, BC = 4 cm và $\hat{A} = \hat{B} = \hat{A C D} = 90 ° .......$

Bài 4.13 trang 78 Toán 9 Tập 1: Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2 m, nhìn thấy hình phản chiếu qua gương B của ngọn cây (cây có gốc ở tại điểm C cách B là 4,8 m, B nằm giữa A và C). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65 m. Tính chiều cao của cây (H.4.24)......

Xem thêm các bài giải bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác:

Bài 11. Tỉ số lượng giác của góc nhọn

Bài 12. Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

Luyện tập chung trang 79

Bài tập cuối chương 4

Bài 13. Mở đầu về đường tròn

Bài 14. Cung và dây của một đường tròn

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

387

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

309

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

242

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

264

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.