Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 9 Một số hệ thức giữa cạnh, góc trong tam giác vuông được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Một số hệ thức giữa cạnh, góc trong tam giác vuông. Mời các bạn đón xem:

Bài tập Toán 9 Một số hệ thức giữa cạnh, góc trong tam giác vuông

A. Bài tập Một số hệ thức giữa cạnh, góc trong tam giác vuông

Bài 1. Cho tam giác MNP vuông tại N. Hệ thức nào sau đây là đúng?

A. MN = MP.sinP;

B. MN = MP.cosP;

C. MN = MP.tanP;

D. MN = MP.cotP.

Hướng dẫn giải

Đáp án đúng là: A

Tam giác MNP vuông tại N nên MN = MP.sinP.

Bài 2. Cho tam giác ABC vuông tại A có AC = 20 cm, $\hat{C}=60°$. Độ dài các cạnh AB, BC lần lượt là

A. $20\sqrt{3}$cm và 40 cm;

B. $20\sqrt{3}$cm và $40\sqrt{3}$ cm;

C. 20 cm và 40 cm;

D. 20 cm và $20\sqrt{3}$cm.

Hướng dẫn giải

Đáp án đúng là: A

Tam giác ABC vuông tại A nên ta có:

⦁AB = AC.tanC = 20.tan60° = $20\sqrt{3}$cm;

⦁AC = BC.cosC, suy ra $BC=\frac{AC}{\cos C}=\frac{20}{\cos 60°}=40$ cm.

Vậy $AB=20\sqrt{3}$ cm, BC = 40 cm. Ta chọn phương án A.

Bài 3. Cho tam giác ABC vuông tại A có đường cao AH và góc B = α. Tìm giá trị α sao cho BH = 3CH.

Hướng dẫn giải

Theo đề bài, ta có hình vẽ sau:

Đặt AH = h.

Xét tam giác ABH vuông tại H, ta có:

BH = AH.cot B = h.cot α.

Xét tam giác ACH vuông tại H, ta có:

CH = AH.cot C = AH.tan B = h.tan α.

BH = 3CH suy ra $\frac{BH}{CH}=\frac{h.\cot \alpha }{h.\tan \alpha }=\frac{\frac{1}{\tan \alpha }}{\tan \alpha }=\frac{1}{{\tan }^2\alpha }=3$

Do đó $\tan \alpha =\frac{\sqrt{3}}{3}=\tan 30°.$

Vậy α = 30°.

Bài 4. Một cây cao có chiều cao 6m. Để hái một buồng cau xuống, phải đặt thang tre sao cho đầu thang tre đạt độ cao đó, khi đó góc của thang tre với mặt đất là bao nhiêu, biết chiếc thang dài 8m.

Hướng dẫn giải

Theo đề bài, ta có hình vẽ sau:

Trong hình vẽ trên, BC là chiều dài của thang tre, AC là chiều cao của cây tre, và AB là khoảng cách từ thang tre tới cây tre.

Xét ∆ABC vuông tại A, ta có:

$\sin B=\frac{AC}{BC}=\frac{6}{8}=\frac{3}{4}$ ⇒ $\hat{B}\approx 48°$

Vậy góc giữa thang tre với mặt đất là 48°.

Bài 5. Một cầu trượt ở công viên có độ dốc là 28° và độ cao là 1,8 m. Tìm độ dài của mặt cầu trượt.

Hướng dẫn giải

Áp dụng hệ thức về cạnh và góc trong tam giác vuông ABC vuông tại A.

Khi đó, độ dài mặt cầu trượt là:

$AB=\frac{1,8}{\sin 28°}\approx 3,83$ (m).

Vậy độ dài của mặt cầu trượt khoảng 3,83 m.

B. Lý thuyết Một số hệ thức giữa cạnh, góc trong tam giác vuông

1. Tính cạnh góc vuông theo cạnh huyền và tỉ số lượng giác của góc nhọn

Ví dụ 1:

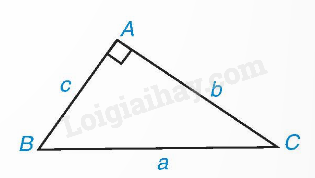
Trong tam giác ABC vuông tại A, ta có:

$\begin{array}{l}b=a.\sin B=a.\cos C;\\ c=a.\sin C=a.\cos B.\end{array}$

2. Tính cạnh góc vuông theo cạnh góc vuông còn lại và tỉ số lượng giác của góc nhọn

Ví dụ 2:

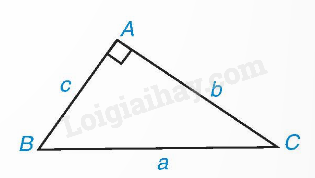
Trong tam giác ABC vuông tại A, ta có:

$\begin{array}{l}b=c.\tan B=c.\cot C;\\ c=b.\tan C=b.\cot B.\end{array}$

3. Áp dụng tỉ số lượng giác của góc nhọn để giải tam giác vuông

Giải tam giác vuông là tìm tất cả độ dài các cạnh và số đo các góc còn lại của tam giác đó.

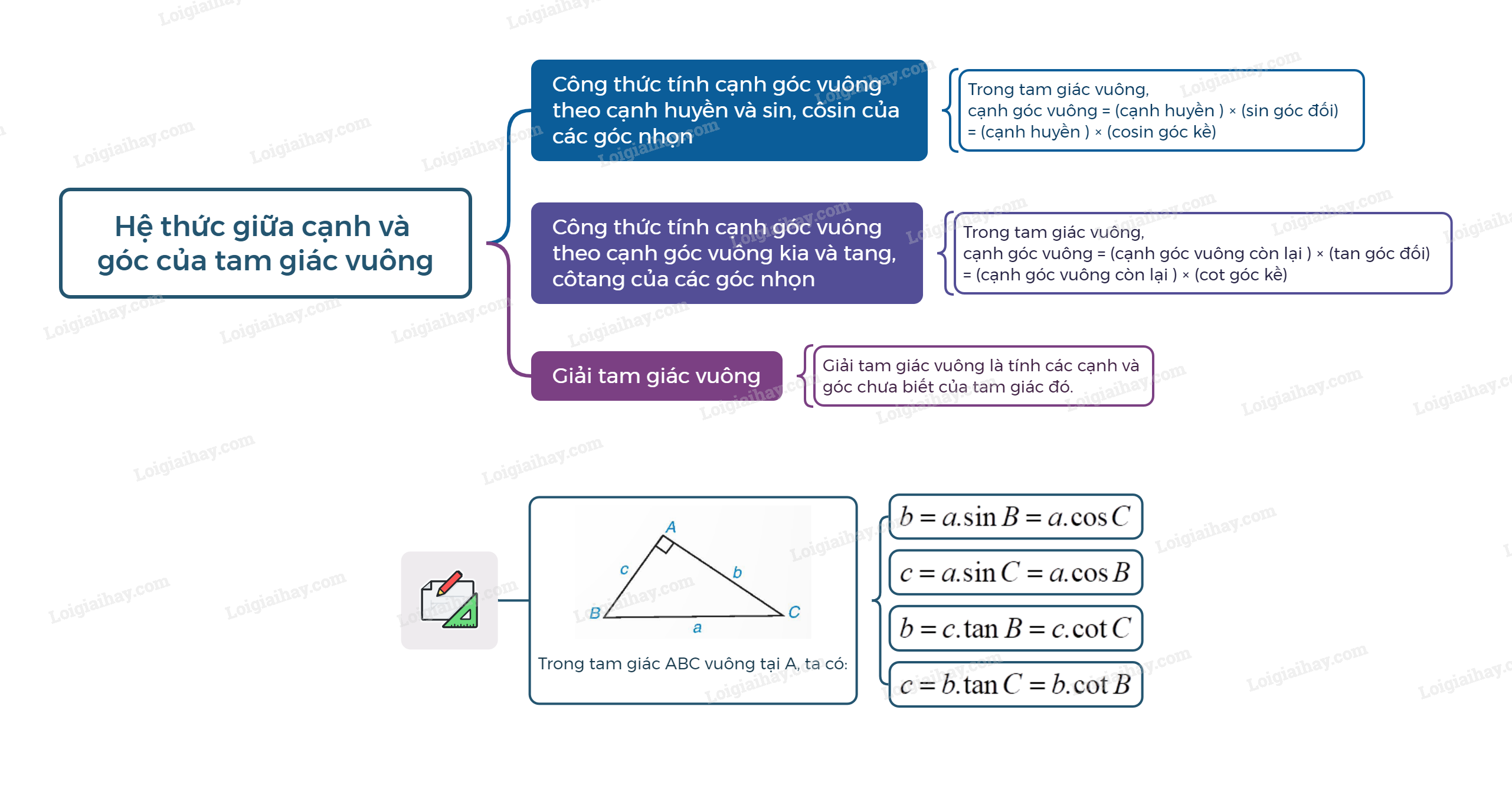
Sơ đồ tư duy Một số hệ thức về cạnh và góc trong tam giác vuông