Với giải Vận dụng 4 trang 65 Toán 9 Tập 1 Chân trời sáng tạo chi tiết trong Bài 1: Tỉ số lượng giác của góc nhọn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 1: Tỉ số lượng giác của góc nhọn

Vận dụng 4 trang 65 Toán 9 Tập 1: a) Vẽ một tam giác vuông có một góc bằng 40°. Đo độ dài các cạnh rồi dùng các số đo để tính các tỉ số lượng giác của góc 40°. Kiểm tra lại các kết quả vừa tính bằng máy tính cầm tay.

b) Vẽ một tam giác vuông có ba cạnh bằng 3 cm, 4 cm, 5 cm. Tính các tỉ số lượng giác của mỗi góc nhọn. Dùng thước đo góc để đo các góc nhọn. Kiểm tra lại các kết quả bằng máy tính cầm tay.

Lời giải:

a) Vẽ tam giác vuông có một góc bằng 40°.

• Chẳng hạn tam giác ABC vuông tại A có $\widehat{B}=40°$ .

• Ta đo độ dài các cạnh của tam giác ABC lần lượt là:

AB = 5 cm, AC = 4 cm và BC ≈ 6,4 cm.

• Từ các độ dài các cạnh đo được, ta có các tỉ số lượng giác của góc 40° như sau:

• Kiểm tra lại bằng máy tính, ta có:

sin 40° ≈ 0,64;                 cos 40° ≈ 0,77;

tan 40° ≈ 0,84;                 cot 40° ≈ 1,19.

Nhận xét: Tỉ số lượng giá sau khi vẽ hình, đo độ dài các cạnh và tính so với tính bằng máy tính cầm tay, ta thu được hai kết quả gần bằng nhau.

b) Vẽ một tam giác vuông có ba cạnh bằng 3 cm, 4 cm, 5 cm.

• Chẳng hạn tam giác MNP vuông có MP = 3 cm, MN = 4 cm, NP = 5 cm.

Ta có MP² + MN² = 3² + 4² = 5² = NP².

Theo định lí Pythagore, ta có tam giác MNP vuông tại M.

• Các tỉ số lượng giác của góc N là:

• Vì tam giác MNP vuông tại M nên $\widehat{N}$  và $\widehat{P}$  là hai góc phụ nhau.

Khi đó, các tỉ số lượng giác của góc P là:

Dùng thước đo góc, ta có: $\widehat{P}\approx 53,1°;\widehat{N}\approx 36,9°$.

Từ các tỉ số lượng giác ở trên, sử dụng máy tính cầm tay, ta thu được kết quả xấp xỉ kết quả khi đo góc.

Lý Thuyết Sử dụng máy tính cầm tay tính tỉ số lượng giác của một góc nhọn

Người ta thường dùng các đơn vị số đo góc là độ (kí hiệu: ${}^0$), phút (kí hiệu: ${}^{\prime }$), giây (kí hiệu: ${}^{″}$).

Ta có thể sử dụng nhiều loại máy tính cầm tay để tính các tỉ số lượng giác của góc nhọn và tính số đo của góc nhọn khi biết một tỉ số lượng giác của nó.

Lưu ý: ta cần đổi đơn vị đo về độ.

Tính các tỉ số lượng giác của các góc nhọn

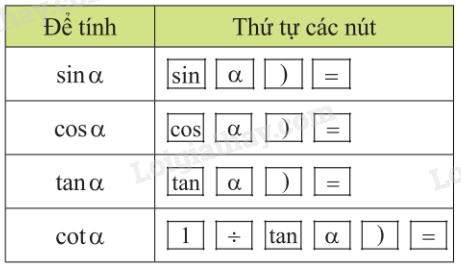
Để tính tỉ số lượng giác của một góc $\alpha$, ta dùng các nút:

Để tính $\cot \alpha$, ta tính $\cot \alpha =\frac{1}{\tan \alpha }$ hoặc $\tan \left({90}^0-\alpha \right)$.

Bảng tóm tắt cách tính tỉ số lượng giác của một góc nhọn

Xác định số đo của góc nhọn khi biết một tỉ số lượng giác của góc đó

Bảng tóm tắt cách tính số đo của một góc nhọn khi biết một tỉ số lượng giác

Để tìm $\alpha$ khi biết $\cot \alpha$, ta tính $\tan \alpha =\frac{1}{\cot \alpha }$ và dùng $\tan \alpha$ để tính $\alpha$.

Một số công thức mở rộng:

+) ${\sin }^2\alpha +{\cos }^2\alpha =1$

+) $\tan \alpha =\frac{\sin \alpha }{\cos \alpha }$

+) $\cot \alpha =\frac{\cos \alpha }{\sin \alpha }$

+) $\tan \alpha .\cot \alpha =1$

+) $\frac{1}{{\cos }^2\alpha }={\tan }^2\alpha +1$

+) $\frac{1}{{\sin }^2\alpha }={\cot }^2\alpha +1$