Với giải sách bài tập Toán 9 Bài 1: Tỉ số lượng giác của góc nhọn sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:

Giải SBT Toán 9 Bài 1: Tỉ số lượng giác của góc nhọn

Bài 1 trang 68 sách bài tập Toán 9 Tập 1: Cho tam giác OAB vuông tại O. Tính các tỉ số lượng giác của góc A trong mỗi trường hợp sau:

a) AB = 7 cm, OB = 4 cm;

b) OA = 5 cm, OB = 9 cm;

c) AB = 11 cm, OB = 6 cm.

Lời giải:

Xét ∆OAB vuông tại O ta có:

⦁ $\sin A=\frac{OB}{AB};\cos A=\frac{OA}{AB};\tan A=\frac{OB}{OA};\cot A=\frac{OA}{OB}.$

⦁ AB² = OA² + OB² (định lí Pythagore)

Suy ra OA² = AB² – OB² và OB² = AB² – OA².

a) Ta có: OA² = AB² – OB² = 7² – 4² = 33. Suy ra $OA=\sqrt{33}\text{ cm}.$

$\sin A=\frac{OB}{AB}=\frac{4}{7};$ $\cos A=\frac{OA}{AB}=\frac{\sqrt{33}}{7};$

$\tan A=\frac{OB}{OA}=\frac{4}{\sqrt{33}}=\frac{4\sqrt{33}}{33};$ $\cot A=\frac{OA}{OB}=\frac{\sqrt{33}}{4}.$

b) Ta có: AB² = OA² + OB² = 5² + 9² = 106. Suy ra $\sqrt{AB}=\sqrt{106}\text{ cm}.$

$\sin A=\frac{OB}{AB}=\frac{9}{\sqrt{106}}=\frac{9\sqrt{106}}{106};$ $\cos A=\frac{OA}{AB}=\frac{5}{\sqrt{106}}=\frac{5\sqrt{106}}{106};$

$\tan A=\frac{OB}{OA}=\frac{9}{5};$ $\cot A=\frac{OA}{OB}=\frac{5}{9};$

c) Ta có: OA² = AB² – OB² = 11² – 6² = 85. Suy ra $\sqrt{OA}=\sqrt{85}\text{ cm}.$

$\sin A=\frac{OB}{AB}=\frac{6}{11};$ $\cos A=\frac{OA}{AB}=\frac{\sqrt{85}}{11};$

$\tan A=\frac{OB}{OA}=\frac{6}{\sqrt{85}}=\frac{6\sqrt{85}}{85};$ $\cot A=\frac{OA}{OB}=\frac{\sqrt{85}}{6}.$

Bài 2 trang 68 sách bài tập Toán 9 Tập 1: Tính giá trị các biểu thức sau:

a) $P=\frac{\tan 60°\cdot \cot 30°}{6\sin 30°};$

b) $Q=\frac{\sin 45°\cdot \cos 45°}{\sin 30°\cdot \cos 60°}.$

Lời giải:

a) $P=\frac{\tan 60°\cdot \cot 30°}{6\sin 30°}=\frac{\sqrt{3}\cdot \sqrt{3}}{6\cdot \frac{1}{2}}=\frac{3}{3}=1.$

b) $Q=\frac{\sin 45°\cdot \cos 45°}{\sin 30°\cdot \cos 60°}=\frac{\frac{\sqrt{2}}{2}\cdot \frac{\sqrt{2}}{2}}{\frac{1}{2}\cdot \frac{1}{2}}=\frac{\frac{2}{4}}{\frac{1}{4}}=\frac{1}{2}\cdot 4=2.$

Bài 3 trang 68 sách bài tập Toán 9 Tập 1: Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45°.

a) cos 69°;

b) cot 83°;

c) sin 77°;

d) tan 51°.

Lời giải:

a) cos 69° = sin (90° ‒ 69°) = sin 21°.

b) cot 83° = tan (90° ‒ 83°) = tan 7°.

c) sin 77° = cos (90° ‒ 77°) = cos 13°.

d) tan 51° = cot (90° ‒ 51°) = cot 39°.

Bài 4 trang 68 sách bài tập Toán 9 Tập 1: Sử dụng máy tính cầm tay, tính tỉ số lượng giác của các góc sau (kết quả làm tròn đến hàng phần nghìn):

a) 74°;

b) 38°;

c) 83°15’.

Lời giải:

Chú ý: Để tính cotα, ta sử dụng công thức cotα = tan(90° – α) hoặc $\cot \alpha =\frac{1}{\tan \alpha }.$

a) Ta có:

b) Ta có:

c) Ta có:

Bài 5 trang 68 sách bài tập Toán 9 Tập 1: Tìm các góc nhọn x, y, z, m trong mỗi trường hợp sau (kết quả làm tròn đến hàng đơn vị của phút):

a) cos x = 0,435;

b) sin y = 0,451;

c) tan z = 4,12;

d) cot m = 0,824.

Lời giải:

Chú ý: Để tính α khi biết cotα, ta tính $\tan \alpha =\frac{1}{\cot \alpha }.$

Bài 6 trang 68 sách bài tập Toán 9 Tập 1: Một cái thang dài 10 m đặt dựa vào tường sao cho chân thang cách tường 6,5 m (Hình 7). Tìm góc α tạo bởi thang và tường (kết quả làm tròn đến hàng đơn vị của độ).

Lời giải:

Gọi C là chân tường. Khi đó, tam giác ABC vuông tại C, ta có:

$\sin \alpha =\sin B=\frac{AC}{AB}=\frac{\mathrm{6,5}}{10}=\mathrm{0,65.}$

Sử dụng máy tính cầm tay bấm liên tiếp các nút $\boxed{SHIFT}\boxed{\sin }\boxed{0}\boxed{,}\boxed{6}\boxed{5}\boxed{=}\boxed{°\text{'}\text{'}\text{'}},$ sau đó làm tròn kết quả đến hàng đơn vị của độ ta được: α ≈ 41°.

Bài 7 trang 68 sách bài tập Toán 9 Tập 1: Một màn hình ti vi có kích thước như trong Hình 8. Tính góc giữa đường chéo và hai cạnh.

Lời giải:

Gọi x và y lần lượt là góc giữa đường chéo và cạnh ngang, cạnh dọc.

Khi đó, ta có: $\tan x=\frac{\mathrm{71,8}}{\mathrm{124,2}},$ suy ra x ≈ 30°.

Mà x + y = 90° nên y = 90° – x ≈ 90° ‒ 30° = 60°.

Bài 8 trang 69 sách bài tập Toán 9 Tập 1: Hai trụ điện cùng chiều cao được dựng thẳng đứng ở hai bên lề đối diện một đại lộ rộng 80 m (AC = 80 m). Từ một điểm M trên mặt đường giữa hai trụ người ta nhìn thấy đỉnh hai trụ điện với các góc nâng lần lượt là 60° và 30°. Tính chiều cao của trụ điện và khoảng cách từ điểm M đến gốc mỗi trụ điện.

Lời giải:

Xét ∆ABM vuông tại A, ta có: $\cot \widehat{AMB}=\frac{AM}{AB}.$

Suy ra $AM=AB\cdot \cot \widehat{AMB}=AB\cdot \cot 60°=\frac{AB\sqrt{3}}{3}\text{ (m).}$

Xét ∆CMD vuông tại C, ta có: $\cot \widehat{CMD}=\frac{CM}{CD}.$

Suy ra $CM=CD\cdot \cot \widehat{CMD}=CD\cdot \cot 30°=CD\sqrt{3}\text{ (m).}$

Mà AB = CD nên $CM=AB\sqrt{3}\text{ (m).}$

Ta có: AC = AM + CM

Suy ra: $80=\frac{AB\sqrt{3}}{3}+AB\sqrt{3}$

Hay $80=AB\left(\frac{\sqrt{3}}{3}+\sqrt{3}\right)$

Do đó $AB=\frac{80}{\frac{\sqrt{3}}{3}+\sqrt{3}}=\frac{80}{\frac{4\sqrt{3}}{3}}=20\sqrt{3}\text{ (m).}$

Như vậy, chiều cao của trụ điện là $20\sqrt{3}$ mét.

Khoảng cách từ điểm M đến trụ điện AB là:

$AM=\frac{AB\sqrt{3}}{3}=\frac{20\sqrt{3}\cdot \sqrt{3}}{3}=20( \text{m}).$

Khoảng cách từ điểm M đến trụ điện CD là:

MC = AC ‒ AM = 80 ‒ 20 = 60 (m).

Lý thuyết Tỉ số lượng giác của góc nhọn

1. Định nghĩa tỉ số lượng giác của một góc nhọn

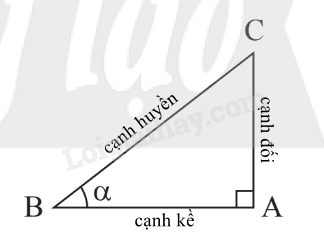
Tip học thuộc nhanh:

Chú ý: Với góc nhọn $\alpha$, ta có:

$0<\sin \alpha <1$; $0<\cos \alpha <1$.

$\cot \alpha =\frac{1}{\tan \alpha }$.

Ví dụ:

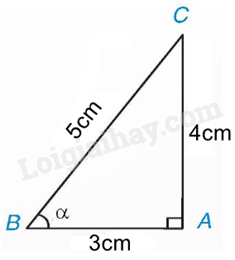
Theo định nghĩa của tỉ số lượng giác, ta có:

$\sin \alpha =\frac{AC}{BC}=\frac{4}{5}$, $\cos \alpha =\frac{AB}{BC}=\frac{3}{5}$, $\tan \alpha =\frac{AC}{AB}=\frac{4}{3}$, $\cot \alpha =\frac{AB}{AC}=\frac{3}{4}$

Bảng giá trị lượng giác của các góc nhọn đặc biệt

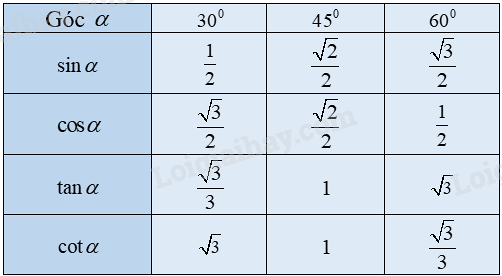
Ví dụ: $P=\frac{\sin {30}^0.\cos {60}^0}{\tan {45}^0}=\frac{\frac{1}{2}.\frac{1}{2}}{1}=\frac{1}{4}$.

2. Tỉ số lượng giác của hai góc phụ nhau

Định lí về tỉ số lượng giác của hai góc phụ nhau

Ví dụ:

$\begin{array}{l}\sin {60}^0=\cos \left({90}^0-{60}^0\right)=\cos {30}^0;\\ \cos {52}^0{30}^{\prime }=\sin \left({90}^0-{52}^0{30}^{\prime }\right)=\sin {37}^0{30}^{\prime };\\ \tan {80}^0=\cot \left({90}^0-{80}^0\right)=\cot {10}^0;\\ \cot {82}^0=\tan \left({90}^0-{82}^0\right)=\tan 8^0.\end{array}$

3. Sử dụng máy tính cầm tay tính tỉ số lượng giác của một góc nhọn

Người ta thường dùng các đơn vị số đo góc là độ (kí hiệu: ${}^0$), phút (kí hiệu: ${}^{\prime }$), giây (kí hiệu: ${}^{″}$).

Ta có thể sử dụng nhiều loại máy tính cầm tay để tính các tỉ số lượng giác của góc nhọn và tính số đo của góc nhọn khi biết một tỉ số lượng giác của nó.

Lưu ý: ta cần đổi đơn vị đo về độ.

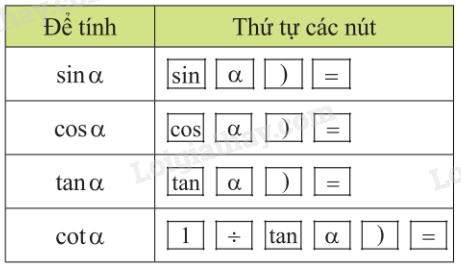
Tính các tỉ số lượng giác của các góc nhọn

Để tính tỉ số lượng giác của một góc $\alpha$, ta dùng các nút:

Để tính $\cot \alpha$, ta tính $\cot \alpha =\frac{1}{\tan \alpha }$ hoặc $\tan \left({90}^0-\alpha \right)$.

Bảng tóm tắt cách tính tỉ số lượng giác của một góc nhọn

Xác định số đo của góc nhọn khi biết một tỉ số lượng giác của góc đó

Bảng tóm tắt cách tính số đo của một góc nhọn khi biết một tỉ số lượng giác

Để tìm $\alpha$ khi biết $\cot \alpha$, ta tính $\tan \alpha =\frac{1}{\cot \alpha }$ và dùng $\tan \alpha$ để tính $\alpha$.

Một số công thức mở rộng:

+) ${\sin }^2\alpha +{\cos }^2\alpha =1$

+) $\tan \alpha =\frac{\sin \alpha }{\cos \alpha }$

+) $\cot \alpha =\frac{\cos \alpha }{\sin \alpha }$

+) $\tan \alpha .\cot \alpha =1$

+) $\frac{1}{{\cos }^2\alpha }={\tan }^2\alpha +1$

+) $\frac{1}{{\sin }^2\alpha }={\cot }^2\alpha +1$

Xem thêm các bài giải SBT Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 3

Bài 1: Tỉ số lượng giác của góc nhọn

Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông

Bài tập cuối chương 4

Bài 1: Đường tròn

Bài 2: Tiếp tuyến của đường tròn