Với giải Thực hành 1 trang 61 Toán 9 Tập 1 Chân trời sáng tạo chi tiết trong Bài 1: Tỉ số lượng giác của góc nhọn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 1: Tỉ số lượng giác của góc nhọn

Thực hành 1 trang 61 Toán 9 Tập 1: Tính các tỉ số lượng giác của góc nhọn A trong mỗi tam giác vuông ABC có $\widehat{B}=90°$ ở Hình 5 (kết quả làm tròn đến hàng phần trăm).

Lời giải:

• Hình 5a:

Xét ∆ABC có  $\widehat{B}=90°,\widehat{A}=\alpha$.

Ta có:

$\sin \alpha =\frac{BC}{AC}=\frac{4}{5}=0,8;$

$\cos \alpha =\frac{AB}{AC}=\frac{3}{5}=0,6;$

$\tan \alpha =\frac{BC}{AB}=\frac{4}{3}\approx 1,33;$

$\cot \alpha =\frac{AB}{BC}=\frac{3}{4}=0,75.$

• Hình 5b:

Xét ∆ABC có $\widehat{B}=90°,\widehat{A}=\alpha$.

Ta có:

$\sin \alpha =\frac{BC}{AC}=\frac{1}{\sqrt{17}}\approx 0,24;$

$\cos \alpha =\frac{AB}{AC}=\frac{4}{\sqrt{17}}\approx 0,97;$

$\tan \alpha =\frac{BC}{AB}=\frac{1}{4}=0,25;$

$\cot \alpha =\frac{AB}{BC}=\frac{4}{1}=4.$

• Hình 5c:

Áp dụng định lí Pythagore vào ∆ABC vuông tại B, ta có:

AC² = AB² + BC² nên BC² = AC² − AB² = 3² − 2² = 5.

Suy ra $BC=\sqrt{5}$.

Xét ∆ABC có $\widehat{B}=90°,\widehat{A}=\alpha$.

Ta có:

$\sin \alpha =\frac{BC}{AC}=\frac{\sqrt{5}}{3}\approx 0,75;$

$\cos \alpha =\frac{AB}{AC}=\frac{2}{3}\approx 0,67;$

$\tan \alpha =\frac{BC}{AB}=\frac{\sqrt{5}}{2}\approx 1,12;$

$\cot \alpha =\frac{AB}{BC}=\frac{2}{\sqrt{5}}\approx 0,89.$

• Hình 5d:

Áp dụng định lí Pythagore vào ∆ABC vuông tại B, ta có:

$A{C}^2=A{B}^2+B{C}^2={\left(\sqrt{10}\right)}^2+{\left(\sqrt{6}\right)}^2=10+6=16$.

Suy ra $AC=\sqrt{16}=4$.

Xét ∆ABC có $\widehat{B}=90°,\widehat{A}=\alpha$.

Ta có:

$\sin \alpha =\frac{BC}{AC}=\frac{\sqrt{6}}{4}\approx 0,61;$

$\cos \alpha =\frac{AB}{AC}=\frac{\sqrt{10}}{4}\approx 0,79;$

$\tan \alpha =\frac{BC}{AB}=\frac{\sqrt{6}}{\sqrt{10}}\approx 0,77;$

$\cot \alpha =\frac{AB}{BC}=\frac{\sqrt{10}}{\sqrt{6}}\approx 1,29.$       

Lý Thuyết Định nghĩa tỉ số lượng giác của một góc nhọn

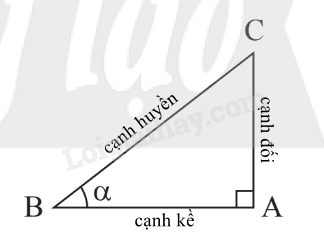
Tip học thuộc nhanh:

Chú ý: Với góc nhọn $\alpha$, ta có:

$0<\sin \alpha <1$; $0<\cos \alpha <1$.

$\cot \alpha =\frac{1}{\tan \alpha }$.

Ví dụ:

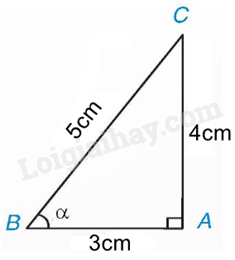
Theo định nghĩa của tỉ số lượng giác, ta có:

$\sin \alpha =\frac{AC}{BC}=\frac{4}{5}$, $\cos \alpha =\frac{AB}{BC}=\frac{3}{5}$, $\tan \alpha =\frac{AC}{AB}=\frac{4}{3}$, $\cot \alpha =\frac{AB}{AC}=\frac{3}{4}$

Bảng giá trị lượng giác của các góc nhọn đặc biệt

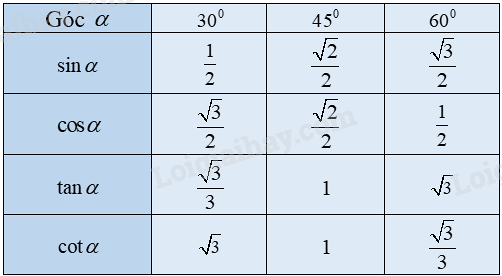
Ví dụ: $P=\frac{\sin {30}^0.\cos {60}^0}{\tan {45}^0}=\frac{\frac{1}{2}.\frac{1}{2}}{1}=\frac{1}{4}$.