Cho góc nhọn mOn = alpha. Lấy hai điểm A và A' trên On, kẻ hai đường thẳng qua A và A' vuông góc với

Cho góc nhọn mOn = alpha. Lấy hai điểm A và A' trên On, kẻ hai đường thẳng qua A và A' vuông góc với

Trịnh Thị Thu Hiền Ngày: 28-07-2024 Lớp 9

146

Với giải Khám phá 1 trang 60 Toán 9 Tập 1 Chân trời sáng tạo chi tiết trong Bài 1: Tỉ số lượng giác của góc nhọn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 1: Tỉ số lượng giác của góc nhọn

Khám phá 1 trang 60 Toán 9 Tập 1: Cho góc nhọn $\hat{m O n} = α .$ Lấy hai điểm A và A' trên On, kẻ hai đường thẳng qua A và A' vuông góc với On cắt Om lần lượt tại B và B'.

Khám phá 1 trang 60 Toán 9 Tập 1 Chân trời sáng tạo | Giải Toán 9

a) Có nhận xét gì về hai tam giác OAB và OA'B' ?

b) So sánh các cặp tỉ số:

$\frac{A B}{O A}$ và $\frac{A^{'} B^{'}}{O A^{'}}; \frac{A B}{O B}$ và $\frac{A^{'} B^{'}}{O B^{'}}; \frac{O A}{O B}$ và $\frac{O A^{'}}{O B^{'}} .$

Lời giải:

a) Xét ∆OAB và ∆OA'B' có:

$\hat{O A B} = \hat{O A^{'} B^{'}} = 90 °$

$\hat{A O B} = \hat{A^{'} O B^{'}}$ (chung gốc O)

Do đó ∆OAB ᔕ ∆OA'B' (g.g).

b) Từ câu a: ∆OAB ᔕ ∆OA'B' suy ra

$\frac{A B}{O A} = \frac{A^{'} B^{'}}{O A^{'}}; \frac{A B}{O B} = \frac{A^{'} B^{'}}{O B^{'}}; \frac{O A}{O B} = \frac{O A^{'}}{O B^{'}} .$

Lý Thuyết Định nghĩa tỉ số lượng giác của một góc nhọn

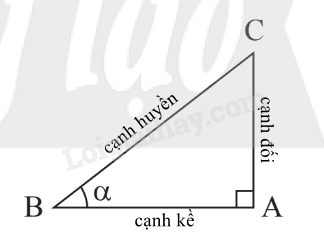
Lý thuyết Tỉ số lượng giác của góc nhọn (Chân trời sáng tạo 2024) | Lý thuyết Toán 9 (ảnh 1)

$s i n α = \frac{c ạ n h đ ố i}{c ạ n h h u y ề n}; c o s α = \frac{c ạ n h k ề}{c ạ n h h u y ề n};$

$t a n α = \frac{c ạ n h đ ố i}{c ạ n h k ề}; c o t α = \frac{c ạ n h k ề}{c ạ n h đ ố i} .$

$\cot α = \frac{1}{\tan α}$ .

$\sin α, \cos α, \tan α, \cot α$ gọi là các tỉ số lượng giác của góc nhọn $α$ .

Tip học thuộc nhanh:

Sin đi học

Cos không hư

Tan đoàn kết

Cotan kết đoàn

Chú ý: Với góc nhọn $α$ , ta có:

$0 < \sin α < 1$ ; $0 < \cos α < 1$ .

$\cot α = \frac{1}{\tan α}$ .

Ví dụ:

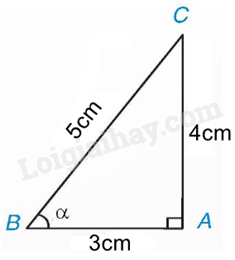
Lý thuyết Tỉ số lượng giác của góc nhọn (Chân trời sáng tạo 2024) | Lý thuyết Toán 9 (ảnh 2)

Theo định nghĩa của tỉ số lượng giác, ta có:

$\sin α = \frac{A C}{B C} = \frac{4}{5}$ , $\cos α = \frac{A B}{B C} = \frac{3}{5}$ , $\tan α = \frac{A C}{A B} = \frac{4}{3}$ , $\cot α = \frac{A B}{A C} = \frac{3}{4}$

Bảng giá trị lượng giác của các góc nhọn đặc biệt

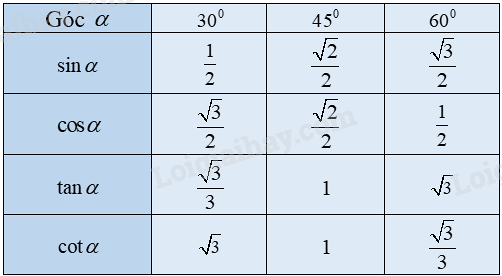
Lý thuyết Tỉ số lượng giác của góc nhọn (Chân trời sáng tạo 2024) | Lý thuyết Toán 9 (ảnh 3)

Ví dụ: $P = \frac{\sin 30^{0} . \cos 60^{0}}{\tan 45^{0}} = \frac{\frac{1}{2} . \frac{1}{2}}{1} = \frac{1}{4}$ .

Xem thêm lời giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:

Khởi động trang 60 Toán 9 Tập 1: Tại một thời điểm, khi những tia nắng chiếu, cây và bóng tạo thành các tam giác vuông như hình bên. Với $\hat{C} = \hat{C^{'}},$ so sánh các tỉ số $\frac{A B}{A C}$ và $\frac{A^{'} B^{'}}{A^{'} C^{'}} .$ .......

Khám phá 1 trang 60 Toán 9 Tập 1: Cho góc nhọn $\hat{m O n} = α .$ Lấy hai điểm A và A' trên On, kẻ hai đường thẳng qua A và A' vuông góc với On cắt Om lần lượt tại B và B'.......

Thực hành 1 trang 61 Toán 9 Tập 1: Tính các tỉ số lượng giác của góc nhọn A trong mỗi tam giác vuông ABC có $\hat{B} = 90 °$ ở Hình 5 (kết quả làm tròn đến hàng phần trăm)........

Vận dụng 1 trang 61 Toán 9 Tập 1: Sử dụng tỉ số lượng giác để giải thích tình huống trong Hoạt động khởi động (trang 60)......

Khám phá 2 trang 62 Toán 9 Tập 1: a) Cho tam giác ABC vuông cân tại A có cạnh góc vuông bằng a (Hình 6a). Tính độ dài cạnh huyền BC theo a, rồi tính các tỉ số lượng giác của góc 45°.......

Thực hành 2 trang 62 Toán 9 Tập 1: Tính giá trị của các biểu thức sau:......

Vận dụng 2 trang 62 Toán 9 Tập 1: Tìm chiều cao của tháp canh trong Hình 7 (kết quả làm tròn đến hàng phần trăm).......

Khám phá 3 trang 63 Toán 9 Tập 1: a) Tính các tỉ số lượng giác của góc α và của góc 90° – α trong Hình 8 theo a, b, c.......

Thực hành 3 trang 63 Toán 9 Tập 1: a) So sánh: sin 72° và cos 18°; cos 72° và sin 18°; tan 72° và cot 18°.......

Vận dụng 3 trang 63 Toán 9 Tập 1: Tia nắng chiếu qua điểm B của nóc tòa nhà tạo với mặt đất một góc x và tạo với cạnh AB của tòa nhà một góc y (Hình 9). Cho biết cos x ≈ 0,78 và cot x ≈ 1,25. Tính sin y và tan y (kết quả làm tròn đến hàng phần trăm).......

Thực hành 4 trang 65 Toán 9 Tập 1: a) Sử dụng máy tính cầm tay, tính tỉ số lượng giác của các góc sau (kết quả làm tròn đến hàng phần nghìn):......

Vận dụng 4 trang 65 Toán 9 Tập 1: a) Vẽ một tam giác vuông có một góc bằng 40°. Đo độ dài các cạnh rồi dùng các số đo để tính các tỉ số lượng giác của góc 40°. Kiểm tra lại các kết quả vừa tính bằng máy tính cầm tay.......

Bài 1 trang 66 Toán 9 Tập 1: Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác của góc B trong mỗi trường hợp sau:......

Bài 2 trang 66 Toán 9 Tập 1: Tính giá trị của các biểu thức sau:.....

Bài 3 trang 66 Toán 9 Tập 1: Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45°:......

Bài 4 trang 66 Toán 9 Tập 1: Sử dụng máy tính cầm tay, tính tỉ số lượng giác của các góc sau:.....

Bài 5 trang 66 Toán 9 Tập 1: Sử dụng máy tính cầm tay, tính tỉ số lượng giác của các góc sau:......

Bài 6 trang 66 Toán 9 Tập 1: Tia nắng chiếu qua nóc của một tòa nhà hợp với mặt đất một góc α. Cho biết tòa nhà cao 21 m và bóng của nó trên mặt đất dài 15 m (Hình 10). Tính góc α (kết quả làm tròn đến độ).......

Bài 7 trang 66 Toán 9 Tập 1: Một cái thang 12 m được đặt vào một bức tường sao cho chân thang cách tường 7 m (Hình 11). Tính góc α tạo bởi thang và tường......

Xem thêm các bài giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 3

Bài 1. Tỉ số lượng giác của góc nhọn

Bài 2. Hệ thức giữa cạnh và góc của tam giác vuông

Bài tập cuối chương 4

Bài 1. Đường tròn

Bài 2. Tiếp tuyến của đường tròn

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

169

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

143

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

116

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.