Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 9 Bài 1: Căn bậc hai và căn bậc ba của số thực chi tiết sách Toán 9 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 1: Căn bậc hai và căn bậc ba của số thực

Khởi động trang 48 Toán 9 Tập 1: Một bàn cờ vua có dạng hình vuông gồm 64 ô vuông nhỏ (Hình 1). Hỏi mỗi cạnh của bàn cờ gồm bao nhiêu cạnh ô vuông nhỏ?

Lời giải:

Mỗi cạnh của bàn cờ gồm 8 cạnh ô vuông nhỏ.

Hoạt động 1 trang 48 Toán 9 Tập 1: Tìm các số thực $x$ sao cho:

a. $x^2=9$

b. $x^2=25$

Lời giải:

a.

$\begin{array}{l}{x}^2=9\\ x^2-9=0\\ \left(x-3\right)\left(x+3\right)=0\end{array}$

Để giải phương trình trên, ta giải hai phương trình:

*) $x-3=0$

$x=3$

*) $x+3=0$

$x=-3$

Vậy phương trình có nghiệm $x=3$ và $x=-3$.

b.

$\begin{array}{l}{x}^2=25\\ x^2-25=0\\ \left(x-5\right)\left(x+5\right)=0\end{array}$

Để giải phương trình trên, ta giải hai phương trình:

*) $x-5=0$

$x=5$

*) $x+5=0$

$x=-5$

Vậy phương trình có nghiệm $x=5$ và $x=-5$.

1.Căn bậc hai của số thực không âm

Luyện tập 1 trang 50 Toán 9 Tập 1: Tìm căn bậc hai của: $256;0,04;\frac{121}{36}$.

Lời giải:

+ Do ${16}^2={\left(-16\right)}^2=256$ nên căn bậc hai của 256 có giá trị bằng 16 và -16.

+ Do $0,2^2={\left(-0,2\right)}^2=0,04$ nên căn bậc hai của 0,04 có giá trị bằng 0,2 và $-0,2$.

+ Do ${\left(\frac{11}{6}\right)}^2={\left(-\frac{11}{6}\right)}^2=\frac{121}{36}$ nên căn bậc hai của $\frac{121}{36}$ có giá trị bằng $\frac{11}{6}$ và $-\frac{11}{6}$.

2. Căn bậc ba

Hoạt động 2 trang 50 Toán 9 Tập 1: Bạn Loan cần làm một chiếc hộp giấy có dạng hình lập phương với thể tích là $64d{m}^3$. Hỏi cạnh của chiếc hộp giấy đó là bao nhiêu decimét? Biết rằng độ dày của tờ giấy để làm hộp là không đáng kể.

Lời giải:

Do $4^3=64$. Vậy cạnh của hộp giấy đó là 4 decimét.

Luyện tập 2 trang 51 Toán 9 Tập 1: Tìm giá trị của:

a. $\sqrt[3]{-8}$;

b. $\sqrt[3]{0,125}$;

c. $\sqrt[3]{0}$.

Lời giải:

a. $\sqrt[3]{-8}=-2$

b. $\sqrt[3]{0,125}=0,5$

c. $\sqrt[3]{0}=0$.3

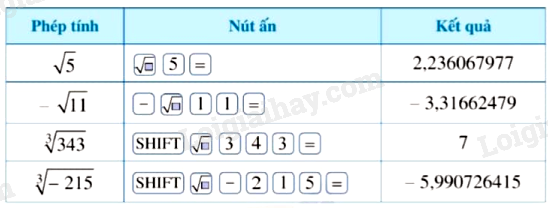
3. Sử dụng máy tính cầm tay để tìm căn bậc hai, căn bậc ba của một số hữu tỉ

Luyện tập 3 trang 52 Toán 9 Tập 1: Sử dụng máy tính cầm tay để tính giá trị (đúng hoặc gần đúng) trong mỗi trường hợp sau:

a. $\sqrt[]{2,37}$

b. $\sqrt[3]{\frac{-7}{11}}$

Lời giải:

a. $\sqrt[]{2,37}=1,539480432\approx 1,54$

b. $\sqrt[3]{\frac{-7}{11}}=-0,8601386275\approx -0,86$.

Bài tập

Bài 1 trang 53 Toán 9 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a. Mỗi số dương có đúng hai căn bậc hai là hai số đối nhau.

b. Số âm không có căn bậc hai.

c. Số âm không có căn bậc ba.

d. Căn bậc ba của một số dương là số dương.

e. Căn bậc ba của một số âm là số âm.

Lời giải:

a. Đúng.

b. Đúng.

c. Sai.

d. Đúng.

e. Đúng.

Bài 2 trang 53 Toán 9 Tập 1: Tìm căn bậc hai của:

a. $289$

b. $0,81$

c. $1,69$

d. $\frac{49}{121}$

Lời giải:

a. Do ${17}^2={\left(-17\right)}^2=289$ nên căn bậc hai của 289 có hai giá trị là 17 và $-17$.

b. Do $0,9^2={\left(-0,9\right)}^2=0,81$ nên căn bậc hai của 0,81 có hai giá trị là 0,9 và $-0,9$.

c. Do $1,3^2={\left(-1,3\right)}^2=1,69$ nên căn bậc hai của 1,69 có hai giá trị là 1,3 và $-1,3$.

d. Do ${\left(\frac{7}{11}\right)}^2={\left(-\frac{7}{11}\right)}^2=\frac{49}{121}$ nên căn bậc hai của $\frac{49}{121}$ có giá trị là $\frac{7}{11}$ và $-\frac{7}{11}$.

Bài 3 trang 53 Toán 9 Tập 1: Tìm căn bậc ba của:

a. 1331

b. -27

c. $-0,216$

d. $\frac{8}{343}$

Lời giải:

a. $\sqrt[3]{1331}=11$.

b. $\sqrt[3]{-27}=-3$.

c. $\sqrt[3]{-0,216}=-0,6$.

d. $\sqrt[3]{\frac{8}{343}}=\frac{2}{7}$.

Bài 4 trang 54 Toán 9 Tập 1: So sánh:

a. $\sqrt[]{\frac{4}{3}}$ và $\sqrt[]{\frac{3}{4}}$.

b. $\sqrt[]{0,48}$ và $0,7$.

c. $\sqrt[3]{-45}$ và $\sqrt[3]{-50}$.

d. $-10$ và $\sqrt[3]{-999}$.

Lời giải:

a. Do $\frac{4}{3}>\frac{3}{4}$ nên $\sqrt[]{\frac{4}{3}}>\sqrt[]{\frac{3}{4}}$.

b. Ta có: $0,7=\sqrt[]{0,49}$. Do $0,48<0,49$ nên $\sqrt[]{0,48}<\sqrt[]{0,49}$ hay $\sqrt[]{0,48}<0,7$.

c. Do $-45>-50$ nên $\sqrt[3]{-45}>\sqrt[3]{-50}$.

d. Ta có: $-10=\sqrt[3]{-1000}$. Do $-1000<-999$ nên $\sqrt[3]{-1000}<\sqrt[3]{-999}$ hay $-10<\sqrt[3]{-999}$.

Bài 5 trang 54 Toán 9 Tập 1: Chứng minh:

a. $\left(2-\sqrt[]{3}\right)\left(2+\sqrt[]{3}\right)=1$

b. $\left(\sqrt[3]{2}+1\right)\left[{\left(\sqrt[3]{2}\right)}^2-\sqrt[3]{2}+1\right]=3$

Lời giải:

a. Ta có:

$\left(2-\sqrt[]{3}\right)\left(2+\sqrt[]{3}\right)=2^2-{\left(\sqrt[]{3}\right)}^2=4-3=1$.

b. Ta có:

$\left(\sqrt[3]{2}+1\right)\left[{\left(\sqrt[3]{2}\right)}^2-\sqrt[3]{2}+1\right]={\left(\sqrt[3]{2}\right)}^3+1^3=2+1=3$.

Bài 6 trang 54 Toán 9 Tập 1: Tính độ dài cạnh huyền của mỗi tam giác vuông trong Hình 2.

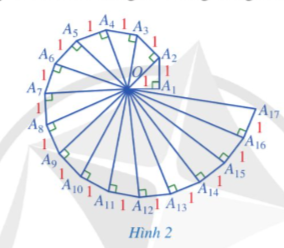
Lời giải:

$O{A}_2=\sqrt{1_{}^2+1_{}^2}=\sqrt{2}$.

$O{A}_3^{}=\sqrt{{\left(\sqrt{2}\right)}_{}^2+1_{}^2}=\sqrt{3}$.

$O{A}_4^{}=\sqrt{{\left(\sqrt{3}\right)}_{}^2+1_{}^2}=2$.

$O{A}_5^{}=\sqrt{2_{}^2+1_{}^2}=\sqrt{5}$.

=> $O{A}_n^{}=\sqrt{n}$.

$O{A}_6^{}=\sqrt{6},$ $O{A}_7^{}=\sqrt{7},O{A}_8^{}=\sqrt{8},$ $O{A}_9^{}=3,$ $O{A}_{10}^{}=\sqrt{10},$ $O{A}_{11}^{}=\sqrt{11},O{A}_{12}^{}=\sqrt{12},$ $O{A}_{13}^{}=\sqrt{13}$, $O{A}_{14}^{}=\sqrt{14},$ $O{A}_{15}^{}=\sqrt{15},$ $O{A}_{16}^{}=4,$ $O{A}_{17}^{}=\sqrt{17}$.

Bài 7 trang 54 Toán 9 Tập 1: Đại Kim tự tháp Giza là Kim tự tháp Ai Cập lớn nhất và là lăng mộ của Vương triều thứ Tư của pharaoh Khufu. Nền kim tự tháp có dạng hình vuông với diện tích khoảng $53052m^2$. Hỏi độ dài cạnh nền của kim tự tháp đó là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

Lời giải:

Gọi độ dài nền của kim tự tháp đó là a (m, a > 0)

Ta có: $a^2=53052$ nên $a\approx 230,3\left(m\right)$.

Vậy độ dài nền của kim tự tháp đó là $230,3\left(m\right)$.

Bài 8 trang 54 Toán 9 Tập 1: Giông bão thổi mạnh, một cây bị gãy gập xuống làm ngọn cây chạm đất và tạo với phương năm ngang một góc ${45}^{\circ }$ (minh họa ở Hình 3). Người ta đo được khoảng cách từ chỗ ngọn cây chạm đất đến gốc cây là $4,5m$. Giả sử cây mọc vuông góc với mặt đất, hãy tính chiều cao của cây đó theo đơn vị mét (làm tròn kết quả đến hàng phần mười).

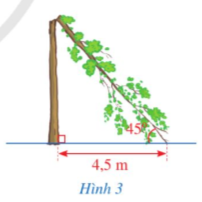
Lời giải:

Chiều cao của cây là: $\frac{4,5}{\cos {45}^{\circ }}=\frac{9\sqrt{2}}{2}\approx 6,4$ (m).

Bài 9 trang 54 Toán 9 Tập 1: Thể tích của một khối bê tông có dạng hình lập phương là khoảng $220348c{m}^3$. Hỏi độ dài cạnh của khối bê tông đó là bao nhiêu centimét (làm tròn kết quả đến hàng phần mười)?

Lời giải:

Gọi độ dài cạnh của khối bê tông là a (cm, a > 0).

Ta có: $a^3=220348$ nên $a\approx 60,4$(cm).

Vậy độ dài cạnh của khối bê tông đó là 60,4 (cm).

Xem thêm các bài giải bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:

Chủ đề 1. Làm quen với bảo hiểm

§1. Căn bậc hai và căn bậc ba của số thực

§2. Một số phép tính về căn bậc hai của số thực

§3. Căn thức bậc hai và căn thức bậc ba của biểu thức đại số

§4. Một số phép biến đổi căn thức bậc hai của biểu thức đại số

Bài tập cuối chương 3

Lý thuyết Căn bậc hai và căn bậc ba của số thực

1. Căn bậc hai của số thực không âm

Chú ý:

- Khi $a>0$, số a có đúng hai căn bậc hai là hai số đối nhau: số dương kí hiệu là $\sqrt{a}$; số âm kí hiệu là $-\sqrt{a}$. Ta gọi $\sqrt{a}$ là căn bậc hai số học của a.

- Căn bậc hai của số 0 bằng 0.

- Số âm không có căn bậc hai.

Ví dụ:

· $\sqrt{81}=9$ nên 81 có hai căn bậc hai là 9 và -9.

· Căn bậc hai số học của 121 là $\sqrt{121}=11$.

Nhận xét: Với hai số a, b không âm, ta có:

- Nếu $a<b$ thì $\sqrt{a}<\sqrt{b}$;

- Nếu $\sqrt{a}<\sqrt{b}$ thì $a<b$.

2. Căn bậc ba

Khái niệm căn bậc ba của một số thực

Chú ý: Mỗi số thực a đều có duy nhất một căn bậc ba.

Nhận xét: ${\left(\sqrt[3]{a}\right)}^3=a$.

Với hai số a, b, ta có:

- Nếu $a<b$ thì $\sqrt[3]{a}<\sqrt[3]{b}$.

- Nếu $\sqrt[3]{a}<\sqrt[3]{b}$ thì $a<b$.

Ví dụ:

$\sqrt[3]{64}=\sqrt[3]{4^3}=4$;

$\sqrt[3]{-27}=\sqrt[3]{{\left(-3\right)}^3}=-3$.

3. Sử dụng máy tính cầm tay để tìm căn bậc hai, căn bậc ba của một số hữu tỉ

Tính căn bậc hai của một số bằng máy tính cầm tay

Tính căn bậc ba của một số bằng máy tính cầm tay

Ta có thể sử dụng loại MTCT thích hợp để tính căn bậc ba của một số.

Ví dụ: