Với lời giải SBT Toán 8 trang 102 Tập 1 Bài 7: Hình vuông sách Cánh diều giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:
Giải SBT Toán 8 Bài 7: Hình vuông
a) Chứng minh các tứ giác và đều là hình vuông.
b) Tứ giác có thể là hình vuông không? Vì sao?
Lời giải:
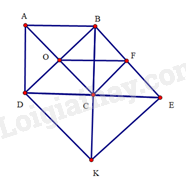
a) Tứ giác là hình vuông suy ra .
Ta có: (hai góc đồng vị) nên (hai góc so le trong) nên .
Từ đó ta chứng minh được tam giác vuông cân tại và tam giác vuông cân tại . Suy ra và .
(c.c.c). Suy ra ta tính được
Tứ giác có nên là hình chữ nhật.
Hình chữ nhật có nên là hình vuông.
Ta có: và nên .
Tứ giác có hai đường chéo và cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
Hình bình hành có nên là hình chữ nhật
Hình chữ nhật có nên là hình vuông
b) Tứ giác có nên không thể là hình vuông.
a)
b) Tứ giác là hình vuông
Lời giải:
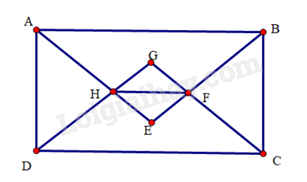
a) Do là hình chữ nhật nên
Mà lần lượt là các tia phân giác của các góc
suy ra
Do đó, các tam giác đều là tam giác vuông cân.
(g.c.g). Suy ra . Mà , suy ra .
Do đó, tam giác vuông cân tại . Suy ra .
Ta có: và nằm ở vị trí đồng vị nên .
b) (hai góc đối đỉnh)
Tứ giác là hình chữ nhật.
Hình chữ nhật có nên là hình vuông.
a)
b) .
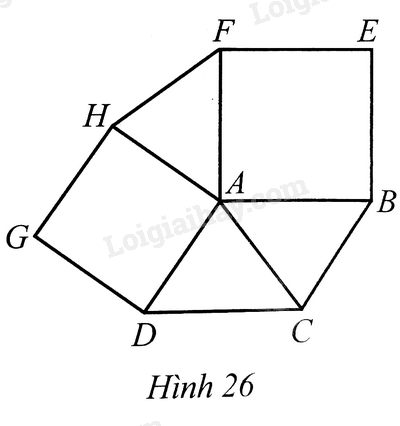
Lời giải:
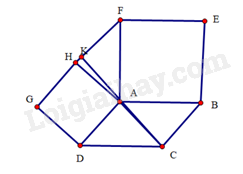
Gọi là giao điểm của và
a) Do và đều là hình vuông nên
Do là hình bình hành nên . Suy ra
Ta chứng minh được và
Suy ra
Xét hai tam giác và , ta có:
Suy ra (c.g.c)
b) Ta có: và nên
Mà (vì ), suy ra
Trong tam giác , ta có: . Suy ra
Vậy hai .
a) Tứ giác là hình gì? Vì sao?
b) Tìm điều kiện của tam giác để tứ giác là hình vuông.
Lời giải:
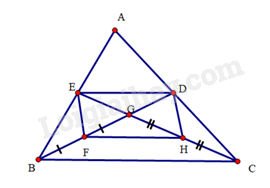
a) Do là trọng tâm tam giác nên . Mà lần lượt là trung điểm của nên .
Tứ giác có hai đường chéo và cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
b) Để hình bình hành là hình vuông thì và
suy ra và .
(c.g.c). Suy ra . Mà , suy ra .
Dễ thấy nếu và thì tứ giác là hình vuông.
Vậy tam giác cân tại có đường trung tuyến , vuông góc với nhau thì tứ giác là hình vuông.
Xem thêm lời giải sách bài tập Toán lớp 8 Cánh diều hay, chi tiết khác:
Xem thêm các bài giải SBT Toán lớp 8 Cánh diều hay, chi tiết khác: