Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 8 Hình vuông, được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Hình vuông. Mời các bạn đón xem:

Bài tập Toán 8 Hình vuông

A. Bài tập Hình vuông

Bài 1. Cho tam giác ABC vuông tại A. Phân giác trong AD của góc A (D ∈ BC ). Vẽ DF ⊥ AC, DE ⊥ AB. Chứng minh tứ giác AEDF là hình vuông.

Hướng dẫn giải

Xét tứ giác AEDF có:

$\widehat{A}=\widehat{E}=\widehat{F}=90°$

Suy ra AEDF là hình chữ nhật (1)

Theo giả thiết ta có: AD là đường phân giác của góc $\widehat{\text{A}}$ .

Suy ra $\widehat{\text{EAD}}=\widehat{\text{DAF}}=45°$ .

Xét ΔAED có: $\widehat{\text{AED}}=90°$

$\widehat{\text{EAD}}=45°$

Suy ra $\widehat{\text{EDA}}=45°$ .

Suy ra ΔAED vuông cân tại E nên AE = ED (2).

Từ (1) và (2) suy ra AEDF là hình vuông.

Vậy AEDF là hình vuông.

Bài 2. Cho hình vuông ABCD. Gọi I, K lần lượt là trung điểm của AD và DC.

a) Chứng minh rằng BI ⊥ AK.

b) Gọi E là giao điểm của BI và AK. Chứng minh rằng $\widehat{EBC}=\widehat{EKD}$ .

Hướng dẫn giải

Xét ∆BAI và ∆ADK có:

AB = AD

$AI=DK=\frac{1}{2}AB=\frac{1}{2}DA$

$\widehat{A}=\widehat{D}$

Suy ra ∆BAI = ∆ADK  (c.g.c)

Suy ra $\widehat{ABI}=\widehat{DAK}$  (góc tương ứng bằng nhau)

Mà $\widehat{IAE}+\widehat{EAB}=90°$

Suy ra $\widehat{ABI}+\widehat{EAB}=90°$

• Xét ∆ABE có $\widehat{EAB}+\widehat{ABE}+\widehat{AEB}=180°$

Suy ra $\widehat{AEB}=180°-\left(\widehat{ABE}+\widehat{BAE}\right)=180°-90°=90°$

Hay AK ⊥ BI (đpcm)

• Xét tứ giác EBCK có $\widehat{KEB}+\widehat{EBC}+\widehat{BCK}+\widehat{CKE}=360°$

Suy ra $\widehat{EBC}+\widehat{EKC}=180°$

Mà $\widehat{AKD}+\widehat{AKC}=180°$ .

Do đó $\widehat{EBC}=\widehat{EKD}$ .

Bài 3. Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy hai điểm D, E sao cho BD = DE = EC. Qua D và E kẻ các đường vuông góc với BC, chúng cắt AB, AC lần lượt ở K và H. Tứ giác KHED là hình gì? Vì sao?

Hướng dẫn giải

Vì tam giác ABC vuông cân tại A nên $\hat{B}=\hat{C}=45°$ .

Tam giác DBK vuông tại D có $\hat{B}=45°$  nên tam giác DBK vuông cân tại D.

Suy ra BD = DK (1)

Chứng minh tương tự ta cũng có tam giác EHC vuông cân tại E.

Suy ra EH = EC (2)

Lại có: BD = DE = EC (gt) (3)

Từ (1), (2) và (3) suy ra KD = DE = HE

Tứ giác KHED có KD // HE (cùng vuông góc với BC) và KD = HE nên tứ giác KHED là hình bình hành.

Mặt khác hình bình hành KHED có hai cạnh bên KD = DE nên KHED là hình thoi.

Mà hình thoi KHED có góc KDE là góc vuông (do giả thiết KD vuông góc BC) nên KHED là hình vuông.

Bài 4. Cho $\widehat{xOy}=90°$ và tia phân giác Om. Lấy điểm A bất kì trên tia Om. Kẻ AB, AC lần lượt vuông góc với Ox, Oy. Chứng minh OBAC là hình vuông.

Hướng dẫn giải

Ta có: AB ⊥ Ox, AC ⊥ Oy nên $\widehat{ABO}=\widehat{ACO}=90°$ .

Lại có $\widehat{xOy}=90°$ nên tứ giác OBAC có ba góc vuông nên là hình chữ nhật.

Mà A nằm trên tia phân giác Om của $\widehat{xOy}$ nên OA là tia phân giác của $\widehat{BOC}$

Do đó hình chữ nhật OBAC là hình vuông.

Bài 5. Cho hình vuông FIHG. Trên các cạnh FI, IH, HG, GF lần lượt lấy các điểm J, M, N, K sao cho FJ = IM = HN = GK.

a) Chứng minh các tam giác KFJ, JIM, MHN và KNG bằng nhau.

b) Tứ giác KJMN là hình gì? Tại sao?

Hướng dẫn giải

a) Vì FIHG là hình vuông nên $\widehat{KFI}=\widehat{FIH}=\widehat{IHG}=\widehat{HGK}=90°$ và FI = IH = HG = GF (1)

Theo giả thiết: FJ = IM = HN = GK (2)

Từ (1) và (2) suy ra: JI = MH = NG = KF

Xét ∆KFJ và ∆JIM có:

$\widehat{KFJ}=\widehat{JIM}=90°$

FJ = IM (giả thiết);

KF = JI (chứng minh trên)

Do đó DKFJ = DJIM (hai cạnh góc vuông)

Chứng minh tương tự ta cũng có:

∆JIM = ∆MHN; ∆MHN = ∆NGK (hai cạnh góc vuông).

Vậy ∆KFJ = ∆JIM = ∆MHN = ∆NGK.

b) Theo câu b, ∆KFJ = ∆JIM nên KJ = JM (hai cạnh tương ứng).

Tương tự, JM = MN, MN = NK

Suy ra KJ = JM = MN = KN.

Do đó tứ giác KJMN là hình thoi.

Do DKFJ = DJIM (theo câu b) nên $\widehat{JKF}=\widehat{MJI}$ (hai góc tương ứng)

Mà $\widehat{KJF}+\widehat{JKF}=90°$ (hai góc nhọn trong tam giác vuông KFJ)

Suy ra $\widehat{KJF}+\widehat{MJI}=90°$

Lại có $\widehat{KJF}+\widehat{KJM}+\widehat{MJI}=180°$ , nên $\widehat{KJM}=90°$

Hình thoi KJMN có nên là hình vuông.

Bài 6. Cho DABC nhọn có AB < AC. Gọi N là trung điểm của AC. Lấy điểm D trên tia BN sao cho ND = NB.

a) Chứng minh ABCD là hình bình hành.

b) Kẻ AP ⊥ BC, CQ ⊥ AD. Chứng minh P, N, Q thẳng hàng.

c) DABC cần thêm điều kiện gì để tứ giác ABCD là hình vuông?

Hướng dẫn giải

a) Tứ giác ACBD có hai đường chéo AC, BD cắt nhau tại trung điểm N của mỗi đường nên là hình bình hành.

b) Ta có: AP ⊥ BC, AQ // BC (do ACBD là hình bình hành)

Suy ra AP ⊥ AQ.

Tứ giác APCQ có ba góc vuông nên là hình chữ nhật.

Khi đó hai đường chéo AC, PQ cắt nhau tại trung điểm của mỗi đường

Mà N là trung điểm của AC nên N là trung điểm của PQ

Do đó P, N, Q thẳng hàng.

c) Để tứ giác ABCD là hình vuông thì cần AB ⊥ BC, AB = BC

Hay DABC vuông cân tại B.

Bài 7: Cho hình vuông ABCD. Trên tia đối của tia BA lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho AE = CF.

a) Chứng minh tam giác EDF vuông cân.

b) Gọi I là trung điểm của EF. Chứng minh BI = DI.

c) Chứng minh A, C, I thẳng hàng.

Bài 8: Cho tứ giác ABCD. Gọi E, F, G, H theo thứu tự là trung điểm của AB, BC, CD, AD. Tìm điều kiện của tứ giác ABCD để tứ giác EFGH là

a) Hình chữ nhật;

b) Hình thoi;

c) Hình vuông.

Bài 9: Cho hình vuông ABCD, lấy M bất kỳ trên cạnh DC. Tia phân giác   cắt CD tại I. Kẻ IH vuông góc với AM tại H, tia IH cắt BC tại K. Chứng minh:

a) ΔABK = ΔAHK ;

b)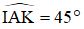 

B. Lý thuyết Hình vuông

1. Định nghĩa

Ta có định nghĩa:

Hình vuông là hình tứ giác có bốn góc vuông và bốn cạnh bằng nhau.

Ví dụ:  Chứng minh tứ giác ABCD là hình vuông.

Hướng dẫn giải

 Ta có $\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90°$  và AB = BC = CD = DA (vì cùng bằng 3 cm).

Suy ra tứ giác ABCD là hình vuông.

2. Tính chất

Ta có định lý sau:

Trong một hình vuông:

- Các cạnh đối song song;

- Hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường;

- Hai đường chéo là các đường phân giác của các góc ở đỉnh.

Ví dụ: Cho hình vuông ABCD có hai đường chéo AC và BD cắt nhau tại O. Chứng minh các tam giác OAB, OBC, OCD, ODA là những tam giác vuông cân.

Hướng dẫn giải

Do ABCD là hình vuông cân nên AC = BD,$\text{AC}\perp \text{BD}$ , AC và BD cắt nhau tại trung điểm O của mỗi đường.

Suy ra các tam giác OAB, OBC, OCD, ODA là những tam giác vuông cân tại O và OA= OB = OC = OD.

Vậy các tam giác OAB, OBC, OCD, ODA là những tam giác vuông cân.

3. Dấu hiệu nhận biết

Ta có những dấu hiệu nhận biết:

- Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông;

- Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông;

- Hình chữ nhật có một đường chéo là đường phân giác cảu một góc là hình vuông.

Ví dụ: Cho đường tròn tâm O. Giả sử AC và BD là hai đường kính của đường trong sao cho $\text{AC}\perp \text{BD}$ . Chứng minh ABCD là hình vuông.

Hướng dẫn giải

Vì tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường nên ABCD là hình bình hành.

Hình bình hành ABCD có AC = BD nên ABCD là hình chữ nhật.

Hình chữ nhật ABCD có hai đừng chéo vuông góc với nhau nên ABCD là hình vuông.

Vậy ABCD là hình vuông.