Với giải sách bài tập Toán 8 Bài 1: Phân thức đại số sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 8. Mời các bạn đón xem:

Giải SBT Toán 8 Bài 1: Phân thức đại số

Giải SBT Toán 8 trang 33

Bài 1 trang 33 SBT Toán 8 Tập 1: Viết điều kiện xác định của mỗi phân thức sau:

a) $\frac{3}{2x\left(5-x\right)}$

b) $\frac{4x}{x^2-4}$

c) $\frac{x}{y^2+2xy}$

d) $\frac{6,4y}{0,4x^2+0,4x}$

Lời giải:

a) Điều kiện xác định của phân thức $\frac{3}{2x\left(5-x\right)}$ là: $2x\left(5-x\right)\ne 0$

b) Điều kiện xác định của phân thức $\frac{4x}{x^2-4}$ là: $x^2-4\ne 0$

c) Điều kiện xác định của phân thức $\frac{x}{y^2+2xy}$ là: $y^2+2xy\ne 0$

d) Điều kiện xác định của phân thức $\frac{6,4y}{0,4x^2+0,4x}$ là: $0,4x^2+0,4x\ne 0$

Bài 2 trang 33 SBT Toán 8 Tập 1: Dùng định nghĩa hai phân thức bằng nhau, hãy giải thích vì sao có thể viết:

a) $\frac{x^2{y}^3}{2x^2{y}^2}=\frac{y}{2}$

b) $\frac{x^2-x-2}{x+1}=\frac{x^2-3x+2}{x-1}$

c) $\frac{x^2-3x+9}{x^3+27}=\frac{1}{x+3}$

Lời giải:

a) Ta có: $x^2{y}^3.2=2x^2{y}^3$ và $2x^2{y}^2.y=2x^2{y}^3$ nên $x^2{y}^3.2=2x^2{y}^2.y$

Vậy $\frac{x^2{y}^3}{2x^2{y}^2}=\frac{y}{2}$

b) Ta có: 

$$\begin{gathered} \left(x^2-x-2\right)\left(x-1\right)=x^3-x^2-2x-x^2+x+2 \\ =x^3-2x^2-x+2 \end{gathered}$$

và 

$$\begin{gathered} \left(x+1\right)\left(x^2-3x+2\right)=x^3-3x^2+2x+x^2-3x+2 \\ =x^3-2x^2-x+2 \end{gathered}$$

Vậy $\frac{x^2-x-2}{x+1}=\frac{x^2-3x+2}{x-1}$

c) Ta có: 

$$\begin{gathered} \left(x^2-3x+9\right)\left(x+3\right)=x^3-3x^2+9x+3x^2-9x+27 \\ =x^3+27 \end{gathered}$$

$\left(x^3+27\right).1=x^3+27$

Vậy $\frac{x^2-3x+9}{x^3+27}=\frac{1}{x+3}$.

Bài 3 trang 33 SBT Toán 8 Tập 1: Mỗi cặp phân thức sau có bằng nhau không? Vì sao?

a) $\frac{x}{5x+5}$ và $\frac{1}{5}$

b) $\frac{-x}{x-5}$ và $\frac{-x\left(x-5\right)}{{\left(x-5\right)}^2}$

c) $\frac{-5}{-x-y}$ và $\frac{5}{x+y}$

d) $\frac{-x}{{\left(x-3\right)}^2}$ và $\frac{x}{{\left(3-x\right)}^2}$

Lời giải:

a) Ta có: $x.5=5x$ và $\left(5x+5\right).1=5x+5$

Do $x.5\ne \left(5x+5\right).1$ nên hai phân thức $\frac{x}{5x+5}$ và $\frac{1}{5}$ không bằng nhau.

b) Ta có: $-x.{\left(x-5\right)}^2=-x{\left(x-5\right)}^2$ và $\left(x-5\right).\left[-x\left(x-5\right)\right]=-x{\left(x-5\right)}^2$

nên $-x.{\left(x-5\right)}^2=\left(x-5\right).\left[-x\left(x-5\right)\right]$

Vậy $\frac{-x}{x-5}=\frac{-x\left(x-5\right)}{{\left(x-5\right)}^2}$

c) Ta có: $-5.\left(x+y\right)=-5\left(x+y\right)$ và $\left(-x-y\right).5=-5\left(x+y\right)$

nên $-5.\left(x+y\right)=\left(-x-y\right).5$

Vậy $\frac{-5}{-x-y}=\frac{5}{x+y}$

d) Ta có: $-x.{\left(3-x\right)}^2=-x{\left(x-3\right)}^2$ và ${\left(x-3\right)}^2.x=x{\left(x-3\right)}^2$

Do $-x{\left(x-3\right)}^2\ne x{\left(x-3\right)}^2$ nên khi $x\ne 0$ và $x\ne 3$ thì hai phân thức $\frac{-x}{{\left(x-3\right)}^2}$ và $\frac{x}{{\left(3-x\right)}^2}$ không bằng nhau

Bài 4 trang 33 SBT Toán 8 Tập 1: Rút gọn mỗi phân thức sau:

a) $\frac{25x^2{y}^3}{35x^3{y}^2}$

b) $\frac{x-y}{y-x}$

c) $\frac{{\left(-x\right)}^5{y}^2}{x^2{\left(-y\right)}^3}$

d) $\frac{x^2-2x}{x^3-4x^2+4x}$

Lời giải:

a) Điều kiện xác định của phân thức là $x\ne 0;y\ne 0$

Ta có: $\frac{25x^2{y}^3}{35x^3{y}^2}=\frac{5.5x^2{y}^3}{5.7x^3{x}^2}=\frac{5y}{7x}$

b) Điều kiện xác định của phân thức là $y-x\ne 0$

Ta có: $\frac{x-y}{y-x}=\frac{-\left(y-x\right)}{y-x}=-1$

c) Điều kiện xác định của phân thức là $x\ne 0;y\ne 0$

Ta có: $\frac{{\left(-x\right)}^5{y}^2}{x^2{\left(-y\right)}^3}=\frac{\left(-1\right).x^5{y}^2}{\left(-1\right).x^2{y}^3}=\frac{x^3}{y}$

d) Điều kiện xác định của phân thức là $x^3-4x^2+4x\ne 0$

Ta có: $\frac{x^2-2x}{x^3-4x^2+4x}=\frac{x\left(x-2\right)}{x\left(x^2-4x+4\right)}=\frac{x\left(x-2\right)}{x{\left(x-2\right)}^2}=\frac{1}{x-2}$

Bài 5 trang 33 SBT Toán 8 Tập 1: Tính giá trị của biểu thức:

a) $A=\frac{x^5{y}^2}{{\left(xy\right)}^3}$ tại $x=1;y=2$

b) $B=\frac{-4\left(x-2\right)x^2}{20\left(2-x\right)y^2}$ tại $x=\frac{1}{2};y=\frac{1}{5}$.

c) $C=\frac{x^2-8x+7}{x^2-1}$ tại $x=-7$

d) $D=\frac{5x^2-10xy+5y^2}{x^2-y^1}$ tại $x=0,5;y=0,6$.

Lời giải:

a) Rút gọn biểu thức: $A=\frac{x^5{y}^2}{{\left(xy\right)}^3}=\frac{x^5{y}^2}{x^3{y}^3}=\frac{x^2}{y}$

ĐKXĐ: ${\left(xy\right)}^3\ne 0$

Giá trị của $A$ khi $x=1;y=2$ là: $\frac{1^2}{2}=\frac{1}{2}$

b) Rút gọn biểu thức: $B=\frac{-4\left(x-2\right)x^2}{20\left(2-x\right)y^2}=\frac{-4.-\left(2-x\right)x^2}{20.\left(2-x\right)y^2}=\frac{x^2}{5y^2}$

ĐKXĐ: $20\left(2-x\right)y^2\ne 0$

Giá trị của $A$ khi $x=\frac{1}{2};y=\frac{1}{5}$ là: $\frac{{\left(\frac{1}{2}\right)}^2}{5.{\left(\frac{1}{5}\right)}^2}=\frac{5}{4}$

c) Rút gọn biểu thức: $C=\frac{x^2-8x+7}{x^2-1}=\frac{\left(x-7\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\frac{x-7}{x+1}$

ĐKXĐ: $x^2-1\ne 0$

Giá trị của $C$ khi $x=-7$ là: $\frac{\left(-7-7\right)}{\left(-7-1\right)}=\frac{7}{4}$

d) Rút gọn biểu thức: 

$$\begin{gathered} D=\frac{5x^2-10xy+5y^2}{x^2-y^2} \\ =\frac{5\left(x^2-2xy+y^2\right)}{\left(x-y\right)\left(x+y\right)} \\ =\frac{5{\left(x-y\right)}^2}{\left(x-y\right)\left(x+y\right)}=\frac{5\left(x-y\right)}{\left(x+y\right)} \end{gathered}$$

ĐKXĐ: $x^2+y^2\ne 0$

Giá trị của $D$ khi $x=0,5;y=0,6$ là: $\frac{5\left(0,5-0,6\right)}{\left(0,5+0,6\right)}=-\frac{5}{11}$

Giải SBT Toán 8 trang 34

Bài 6 trang 34 SBT Toán 8 Tập 1: Quy đồng mẫu thức các phân thức trong mỗi trường hợp sau:

a) $\frac{2}{15x^3{y}^2};\frac{y}{10x^4{z}^3}$ và $\frac{x}{20y^{3}z}$

b) $\frac{x}{2x+6}$ và $\frac{4}{x^2-9}$

c) $\frac{2x}{x^3-1}$ và $\frac{x-1}{x^2+x+1}$

d) $\frac{x}{1+2x+x^2}$ và $\frac{3}{5x^2-5}$

Lời giải:

a) Ta có:

Chọn MTC là: $60x^4{y}^3{z}^3$.

Nhân tử phụ của ba mẫu thức $15x^3{y}^2;10x^4{z}^3;20y^{3}z$ lần lượt là: $4xy{z}^3;6y^3;3x^4{z}^2$

Vậy: $\frac{2}{15x^3{y}^2}=\frac{2\left(4xy{z}^3\right)}{15x^3{y}^2.4xy{z}^3}=\frac{8xy{z}^3}{60x^4{y}^3{z}^3}$

 $\frac{y}{10x^4{z}^3}=\frac{y.6y^3}{10x^4{z}^3}=\frac{6y^4}{60x^4{y}^3{z}^3}$

$\frac{x}{20y^{3}z}=\frac{x.3x^4{z}^2}{20y^{3}z.3x^4{z}^2}=\frac{3x^5{z}^2}{60x^4{y}^3{z}^3}$

b) Ta có: $2x+6=2\left(x+3\right);x^2-9=\left(x+3\right)\left(x-3\right)$

Chọn MTC là: $2\left(x^2-9\right)$

Nhân tử phụ của hai mẫu thức $2x+6;x^2-9$ lần lượt là $\left(x-3\right);2$

Vậy: $\frac{x}{2x+6}=\frac{x\left(x-3\right)}{2\left(x+3\right)\left(x-3\right)}=\frac{x^2-3x}{2\left(x^2-9\right)}$

  $\frac{4}{x^2-9}=\frac{4.2}{2\left(x+3\right)\left(x-3\right)}=\frac{8}{2\left(x^2-9\right)}$

c) Ta có: $x^3-1=\left(x-1\right)\left(x^2+x+1\right)$

Chọn MTC là: $x^3-1$

Nhân tử phụ của hai mẫu thức $x^3-1;x^2+x+1$ lần lượt là: $1;\left(x-1\right)$

Vậy: $\frac{2x}{x^3-1}$

 $\frac{x-1}{x^2+x+1}=\frac{\left(x-1\right)\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}=\frac{{\left(x-1\right)}^2}{x^3-1}$

d) Ta có: 

$$\begin{gathered} 1+2x+x^2={\left(x+1\right)}^2; \\ 5x^2-5=5\left(x^2-1\right)=5\left(x-1\right)\left(x+1\right) \end{gathered}$$

Chọn MTC là: $5\left(x-1\right){\left(x+1\right)}^2$

Nhân tử phụ của hai mẫu thức $1+2x+x^2;5x^2-5$ lần lượt là: $5\left(x-1\right);x+1$

Vậy: $\frac{x}{1+2x+x^2}=\frac{x.5.\left(x-1\right)}{5\left(x-1\right){\left(x+1\right)}^2}=\frac{5x\left(x-1\right)}{5\left(x-1\right){\left(x+1\right)}^2}$

          $\frac{3}{5x^2-5}=\frac{3\left(x+1\right)}{5\left(x-1\right){\left(x+1\right)}^2}$

Bài 7 trang 34 SBT Toán 8 Tập 1: Chứng tỏ giá trị của biểu thức sau không phụ thuộc vào giá trị của biến (với $a$ là một số):

a) $\frac{x^2-y^2}{\left(x+y\right)\left(ax-ay\right)}\left(a\ne 0\right)$

b) $\frac{{\left(x+a\right)}^2-x^2}{2x+a}$

Lời giải:

a) Ta có: $\frac{x^2-y^2}{\left(x+y\right)\left(ax-ay\right)}=\frac{\left(x-y\right)\left(x+y\right)}{\left(x+y\right).a\left(x-y\right)}=\frac{1}{a}$

Vậy biểu thức đã cho không phụ thuộc vào giá trị của biến.

b) Ta có: $\frac{{\left(x+a\right)}^2-x^2}{2x+a}=\frac{\left(x+a-x\right)\left(x+a+x\right)}{2x+a}=\frac{a\left(2x+a\right)}{2x+a}=a$

Vậy biểu thức đã cho không phụ thuộc vào giá trị của biến.

Bài 8 trang 34 SBT Toán 8 Tập 1: Một miếng bìa có dạng hình vuông với độ dài xạnh là $x$ (cm). Người ta cắt đi ở mỗi góc của miếng bìa một hình vuông sao cho bốn hình vuông bị cắt đi có cùng độ dài cạnh là $y$ (cm) với $0<2y<x$ (Hình 2).

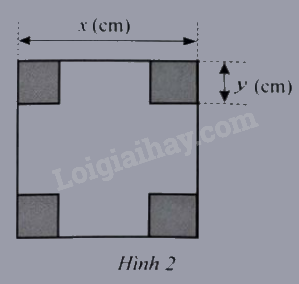
a) Viết phân thức biểu thị tỉ số diện tích của miếng bìa ban đầu và phần miếng bìa còn lại sau khi bị cắt.

b) Tính giá trị của phân thức đó tại $x=4;y=1$

Lời giải:

a) Diện tích của miếng bìa ban đầu là: $x^2\left(c{m}^2\right)$

Diện tích của phần bìa còn lại sau khi cắt là: $x^2-4y^2\left(c{m}^2\right)$

Phân thức biểu thị tỉ số diện tích của miếng bìa ban đầu và phần miếng bìa còn lại sau khi bị cắt là: $\frac{x^2}{x^2-4y^2}$

b) Giá trị của phân thức $\frac{x^2}{x^2-4y^2}$ tại $x=4;y=1$ là: $\frac{4^2}{4^2-{4.1}^2}=\frac{4}{3}$

Xem thêm các bài giải SBT Toán lớp 8 Cánh diều hay, chi tiết khác:

Bài tập cuối chương 1

Bài 1: Phân thức đại số

Bài 2: Phép cộng, phép trừ phân thức đại số

Bài 3: Phép nhân, phép chia phân thức đại số

Bài tập cuối chương 2

Lý thuyết Phân thức đại số

1. Khái niệm

Một phân thức đại số (hay còn gọi là phân thức) là một biểu thức có dạng $\frac{P}{Q}$, trong đó P, Q là những đa thức và Q khác đa thức 0.

P được gọi là tử thức (hay tử), Q được gọi là mẫu thức (hay mẫu).

Chú ý: Mỗi đa thức được coi là một phân thức với mẫu thức bằng 1. Đặc biệt, mỗi số thực cũng là một phân thức đại số.

Ví dụ: $\frac{2x+1}{x-3};\frac{ab}{a+b};x^2+3x+2;\sqrt{2}$ là các phân thức đại số.

$\sqrt{x};\sqrt[3]{x}$ không phải là phân thức vì $\sqrt{x};\sqrt[3]{x}$ không phải là đa thức.

Hai phân thức bằng nhau 

Ta nói hai phân thức $\frac{A}{B}$ và $\frac{C}{D}$ bằng nhau 

nếu A.D = B.C. Khi đó, ta viết $\frac{A}{B}=\frac{C}{D}$.

Ví dụ: Hai phân thức $\frac{x{y}^2}{xy+y}$ và $\frac{xy}{x+1}$ bằng nhau.

2. Tính chất

Khi nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.

$\frac{A}{B}=\frac{A.C}{B.C}$ (C là một đa thức khác đa thức không).

Khi chia cả tử và mẫu của một phân thức cho cùng một nhân tử chung của chúng thì được một phân thức bằng phân thức đã cho.

$\frac{A}{B}=\frac{A:D}{B:D}$ (D là một đa thức nhân tử chung).

Ví dụ: Để biến đổi phân thức $\frac{x-y}{y^2-x^2}$ thành $\frac{-1}{x+y}$, ta chia cả tử và mẫu của phân thức $\frac{x-y}{y^2-x^2}$ cho y – x, khi đó $\frac{x-y}{y^2-x^2}=\frac{-(y-x)}{(y-x)(y+x)}=\frac{-1}{x+y}$

3. Rút gọn phân thức

Muốn rút gọn một phân thức, ta có thể làm như sau:

Bước 1. Phân tích tử và mẫu thành nhân tử (nếu cần)

Bước 2. Tìm nhân tử chung của tử và mẫu rồi chia cả tử và mẫu cho nhân tử chung đó.

Ví dụ: $\frac{x-y}{y^2-x^2}=\frac{-(y-x)}{(y-x)(y+x)}=\frac{-1}{x+y}$

4. Quy đồng mẫu thức của nhiều phân thức

Mẫu thức chung (MTC) chia hết cho mẫu thức của mỗi phân thức đã cho.

Tìm mẫu thức chung:

Bước 1. Phân tích mẫu của mỗi phân thức đã cho thành nhân tử (nếu cần)

Bước 2. Chọn mẫu thức chung.

Quy đồng mẫu thức hai hay nhiều phân thức:

Bước 1. Phân tích mẫu của mỗi phân thức thành nhân tử rồi tìm MTC

Bước 2. Tìm nhân tử phụ của mỗi mẫu thức (bằng cách chia MTC cho từng mẫu

Bước 3. Nhân cả tử và mẫu của mỗi phân thức đã cho với nhân tử phụ tương ứng

Ví dụ: Quy đồng mẫu thức hai phân thức $\frac{1}{x^2+x}$ và $\frac{1}{x^2-x}$

MTC là:

Ta có: $\left[x\left(x+1\right)\left(x--1\right)\right]:\left[x(x+1)\right]=x-1;\left[x\left(x+1\right)\left(x--1\right)\right]:\left[x(x-1)\right]=x+1$

Khi đó: $\frac{1}{x^2+x}=\frac{1}{x(x+1)}=\frac{x-1}{x(x+1)(x-1)};\frac{1}{x^2-x}=\frac{1}{x(x-1)}=\frac{x+1}{x(x-1)(x+1)}$

5. Điều kiện xác định, giá trị của phân thức đại số

Xác định điều kiện xác định của phân thức $\frac{A}{B}$

Điều kiện xác định của phân thức $\frac{A}{B}$ là điều kiện của biến để mẫu thức B khác 0.

Giá trị của phân thức đại số

Cho phân thức đại số $\frac{A}{B}$. Giá trị của biểu thức $\frac{A}{B}$ tại những giá trị cho trước của các biến để giá trị của mẫu thức khác 0 được gọi là giá trị của phân thức $\frac{A}{B}$ tại những giá trị cho trước của biến đó.

Ví dụ: Phân thức P = $\frac{x+3}{x-1}$ xác định khi $x-1\ne 0$hay $x\ne 1$

Tại x = 3, $P=\frac{3+3}{3-1}=\frac{6}{2}=3$