Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 10 Bài 3: Tích của một số với một vecto chi tiết sách Toán 10 Tập 1 Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 3: Tích của một số với một vecto
1. Tích của một số với một vecto và các tính chất
Giải toán lớp 10 trang 94 Tập 1 Chân trời sáng tạo
Lời giải:
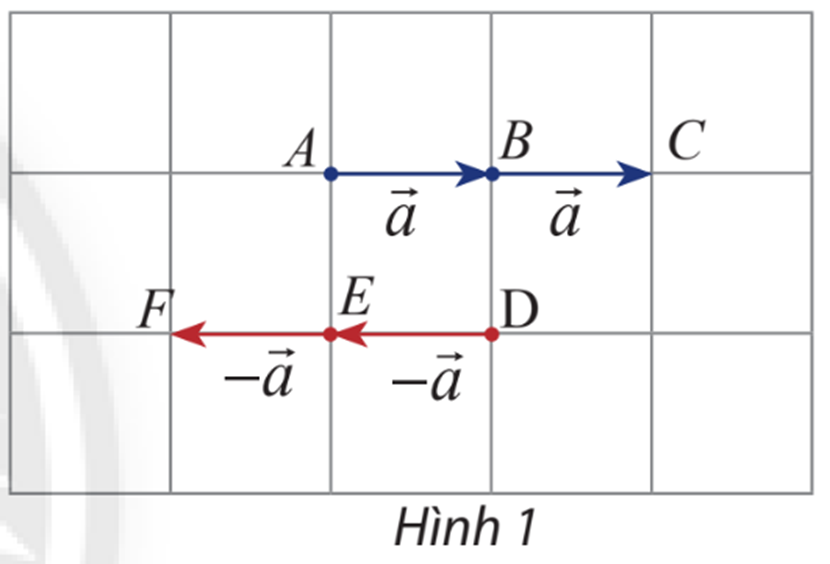
Dựa vào hình 1 ta thấy
Vectơ có độ dài bằng 2 lần vectơ và cùng hướng với vectơ
Vectơ có độ dài bằng 2 lần vectơ và cùng hướng với vectơ
Giải toán lớp 10 trang 95 Tập 1 Chân trời sáng tạo
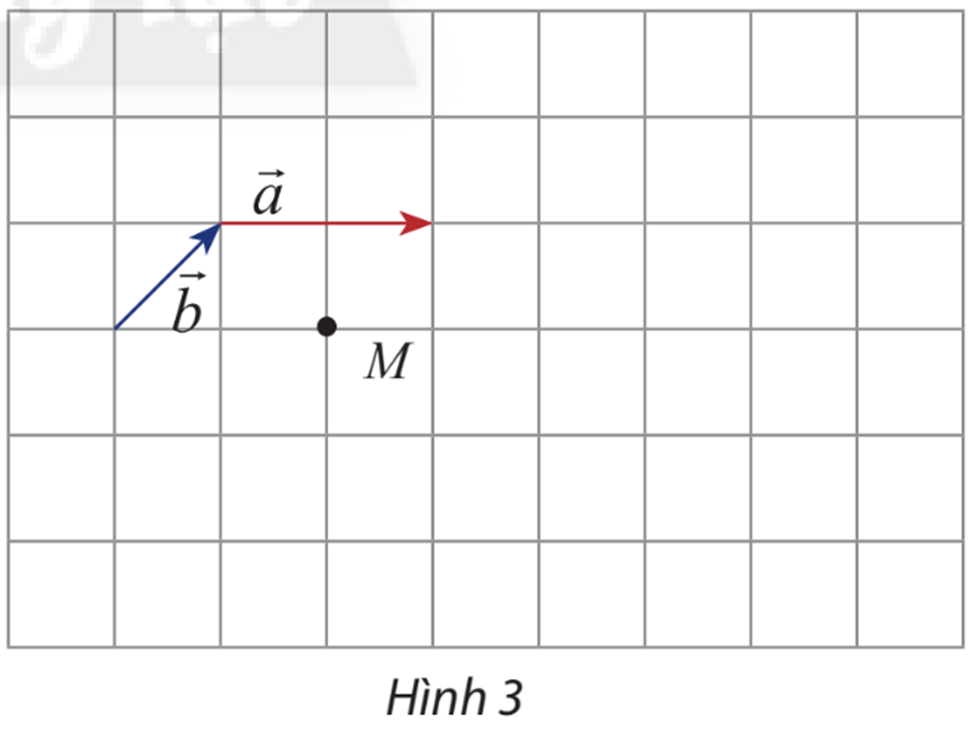
Thực hành 1 trang 95 Toán lớp 10: Cho hai vectơ cho hai vectơ và điểm M như hình 3.
a) Hãy vẽ vectơ
b) Cho biết mỗi ô có cạnh bằng 1. Tính: .
Phương pháp giải:
Bước 1: Xác định hướng của vectơ
Bước 2: Xác định tỉ lệ độ dài
Lời giải:
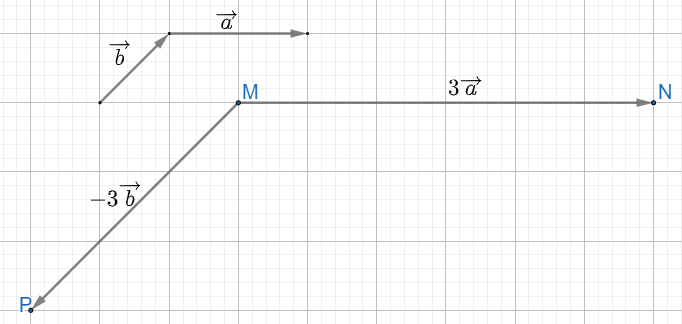
a) có độ dài bằng 3 lần vectơ , cùng hướng với vectơ
Suy ra, từ điểm M vẽ vectơ MN với độ dài là 6 ô vuông và có hướng từ trái sang phải
có độ dài bằng 3 lần vectơ , ngược hướng với vectơ
Suy ra, từ điểm M vẽ vectơ MP với độ dài là 3 đường chéo ô vuông và có hướng từ trên xuống dưới chếch sang trái
b) Hình vuông với cạnh bằng 1 thì ta tính được đường chéo có độ dài là ; . Suy ra:
; ;
Từ điểm cuối của vectơ vẽ một vectơ bằng vectơ ta có
Áp dụng định lý cosin ta tính được độ dài của vectơ là
Phương pháp giải:
Sử dụng quy tắc 3 điểm
Lời giải:
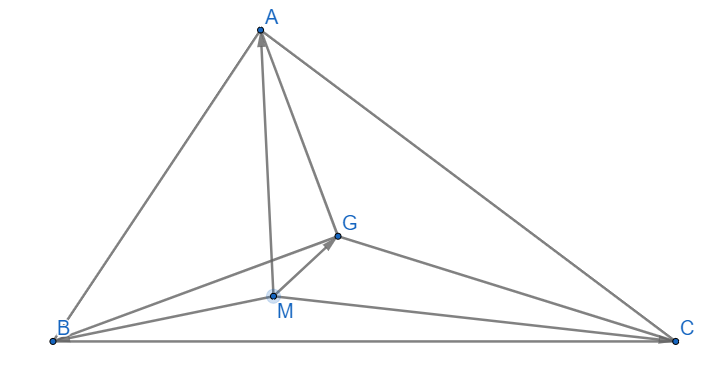
(đpcm) ( Vì G là trọng tâm của tam giác ABC nên )

Lời giải:
Ta thấy hai hướng đông và tây là ngược nhau và tỉ số độ dài

2. Điều kiện để hai vecto cùng phương
Giải toán lớp 10 trang 96 Tập 1 Chân trời sáng tạo
Lời giải:
vectơ có độ dài gấp lần vectơ và cùng hướng với vectơ
+) Nếu hai vectơ và cùng hướng thì hai vectơ và cùng hướng và ngược lại
+) . Suy ra hai vectơ và có cùng độ dài
Phương pháp giải:
Sử dụng tính chất trung điểm và quy tắc ba điểm
với I là trung điểm AB
G là trung điểm IJ.
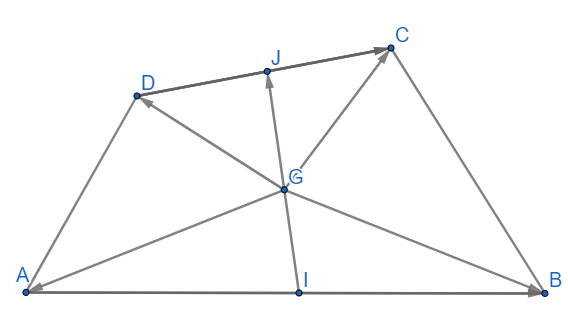
Lời giải:
Ta có:
G là trung điểm của đoạn thẳng IJ
Vậy I, G, J thẳng hàng
Bài tập
Giải toán lớp 10 trang 97 Tập 1 Chân trời sáng tạo
Phương pháp giải:
a) Sử dụng quy tắc ba điểm và tính chất trung điểm
b) Sử dụng tính chất của bình bình hành
Lời giải:
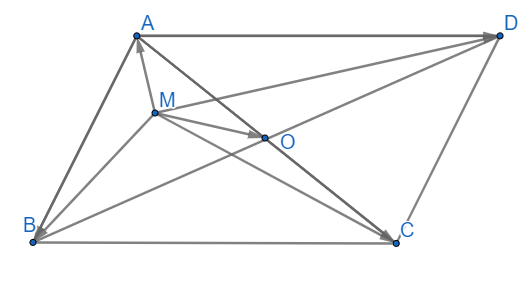
a)
(luôn đúng)
(vì O là giao điểm 2 đường chéo nên là trung điểm của AB, CD)
b) ABCD là hình bình hành nên ta có
Suy ra (đpcm)
Phương pháp giải:
Chèn điểm M: ,
Tính chất trung điểm
Lời giải:
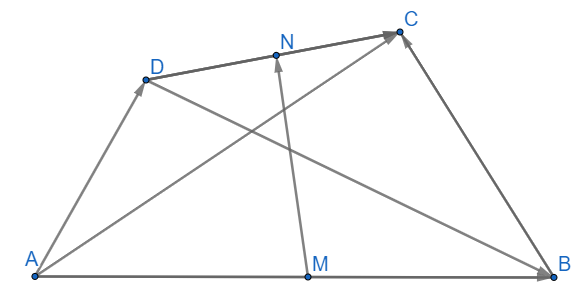
a)(đpcm)
b)
Mặt khác ta có:
Suy ra
Cách 2:
Bài 3 trang 97 Toán lớp 10: Cho hai điểm phân biệt A và B. Xác định điểm M sao cho
Phương pháp giải:
Bước 1: Xác định hướng của hai vectơ
Bước 2: Xác định tỉ số độ dài
Lời giải:
Cách 1:
và hai vectơ ngược hướng
Suy ra M nằm giữa AB sao cho
Cách 2:
Vậy A, M, B thẳng hàng, M nằm giữa A và B sao cho
Phương pháp giải:
Sử dụng quy tắc ba điểm và tính chất trung điểm
(với O là trung điểm của AB)
Lời giải:
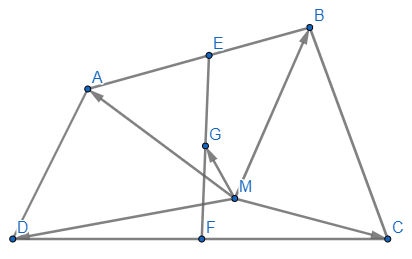
(đpcm)
Lời giải:
Vecto là vecto vận tốc của máy bay A và máy bay b.
Do đó lần lượt là độ lớn của vecto vận tốc tương ứng.
Ta có:
Hai hướng Đông Bắc và Tây Nam là ngược nhau, do đó
Bài 6 trang 97 Toán lớp 10: Cho 2 điểm phân biệt A và B
a) Xác định điểm O sao cho
b) Chứng minh rằng với mọi điểm M, ta có
Phương pháp giải:
a) Chèn điểm:
Từ đó tìm theo đã biết
b) Chèn điểm O, làm xuất hiện ở vế trái.
Lời giải:
a)
Vậy O thuộc đoạn AB sao cho
b) Ta có:
Bài 7 trang 97 Toán lớp 10: Cho tam giác ABC
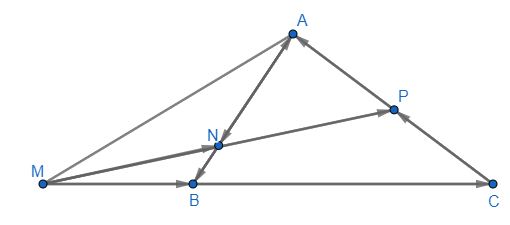
a) Xác định các điểm M, N, P thỏa mãn:
b) Biểu thị mỗi vectơ theo hai vectơ
c) Chứng minh ba điểm M, N, P thẳng hàng
Phương pháp giải:
a) Xác định hướng và tỉ số độ dài
và cùng hướng; tỉ số độ dài
b) Phân tích theo hai vecto
c) thẳng hàng
Lời giải:
a) Ta có:
+) và cùng hướng; tỉ số độ dài
nằm ngoài đoạn thẳng BC sao cho
+)
thuộc đoạn thẳng AB và
+)
là trung điểm của CA
b)
c) Ta có:
Vậy thẳng hàng
Lý thuyết Tích của một số với một vectơ
1. Tích của một số với một vectơ và các tính chất
Cho số k ≠ 0 và . Tích của số k với là một vectơ, kí hiệu là .
Vectơ cùng hướng với nếu k > 0, ngược hướng với nếu k < 0 và có độ dài bằng .
Ta quy ước và .
Người ta còn gọi tích của một số với một vectơ là tích của một vectơ với một số.
Ví dụ: Cho tam giác ABC có D, E, F lần lượt là trung điểm các cạnh AB, BC, CA. Tìm các vectơ bằng: .
Hướng dẫn giải
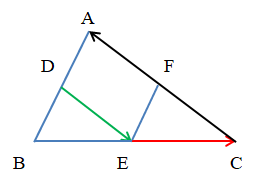
+ Vectơ bằng :
Tam giác ABC có D, E lần lượt là trung điểm của AB, BC.
Do đó DE là đường trung bình của tam giác ABC.
Suy ra DE // AC và 2DE = AC.
Vì k = 2 > 0 nên vectơ cần tìm cùng hướng với và có độ dài bằng 2DE.
Ta có cùng hướng với và 2DE = AC.
Do đó .
+ Vectơ bằng :
Ta có F là trung điểm CA.
Do đó FA = CF = .
Vì k = < 0, nên vectơ cần tìm ngược hướng với và có độ dài bằng .
Ta có ngược hướng với và AF = FC = .
Do đó .
+ Vectơ bằng :
Ta có E là trung điểm BC.
Do đó CB = 2EC.
Vì k = –2 < 0, nên vectơ cần tìm ngược hướng với và có độ dài bằng 2EC.
Ta có ngược hướng với và CB = 2EC.
Do đó .
Tính chất:
Với hai vectơ và bất kì, với mọi số thực h và k, ta có:
+) ;
+) ;
+) ;
+) ;
+) .
Ví dụ: Ta có:
a) ;
b) ;
c) ;
d) .
Ví dụ: Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi .
Hướng dẫn giải
Ta có
(quy tắc ba điểm)
⇔ G là trọng tâm của tam giác ABC (đpcm).
2. Điều kiện để hai vectơ cùng phương
Hai vectơ và () cùng phương khi và chỉ khi có số k sao cho .
Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi có số k ≠ 0 để .
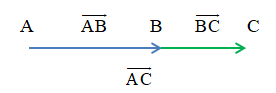
Chú ý: Cho hai vectơ và không cùng phương. Với mỗi luôn tồn tại duy nhất cặp số thực (m; n) sao cho .
Ví dụ: Cho tam giác ABC. Lấy các điểm M, N, P sao cho , , .
a) Biểu diễn theo .
b) Biểu diễn theo .
c) Chứng minh rằng: 3 điểm M, N, P thẳng hàng.
Hướng dẫn giải
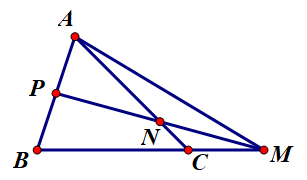
a) Ta có .
Mà cùng hướng (do k = 3 > 0)
Do đó ba điểm B, C, M thẳng hàng và C nằm giữa B, M sao cho MB = 3MC.
Ta có nên P là trung điểm AB.
Do đó AP = AB.
Mà cùng hướng.
Suy ra .
Ta có:
Ta có
.
Ta có
Vậy (1)
b) Ta có .
Do đó hay NA = 3NC.
Khi đó ta có AN = AC.
Mà ngược hướng (do k = ‒3 < 0).
Do đó ba điểm A, N, C thẳng hàng và N nằm giữa hai điểm A và C sao cho
Suy ra .
Ta có
Vậy (2)
c) Từ (1), ta suy ra .
Từ (2), ta suy ra .
Do đó ta có hay .
Vậy ba điểm M, N, P thẳng hàng.
Xem thêm các bài giải SGK Toán 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Tổng và hiệu của hai vecto