Với giải HĐ Khám phá trang 94 Toán lớp 10 Chân trời sáng tạo chi tiết trong Bài 3: Tích của một số với một vecto học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 3: Tích của một số với một vecto

HĐ Khám phá 1 trang 94 Toán lớp 10: Cho vectơ $\overrightarrow{a}$. Hãy xác định độ dài và hướng của hai vectơ $\overrightarrow{a}+\overrightarrow{a},\left(-\overrightarrow{a}\right)+\left(-\overrightarrow{a}\right)$: (Hình 1)

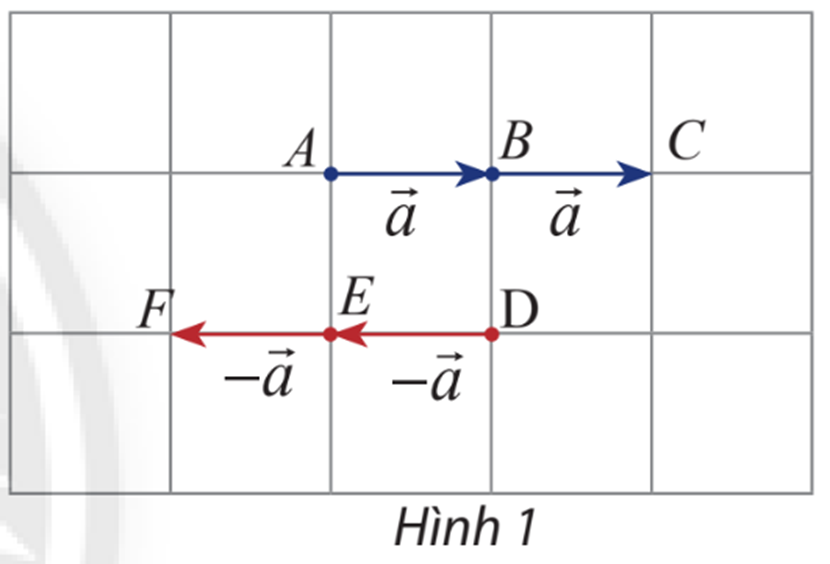
Lời giải:

Dựa vào hình 1 ta thấy

Vectơ $\overrightarrow{a}+\overrightarrow{a}=\overrightarrow{AC}$ có độ dài bằng 2 lần vectơ $\overrightarrow{a}$và cùng hướng với vectơ $\overrightarrow{a}$

Vectơ $\left(-\overrightarrow{a}\right)+\left(-\overrightarrow{a}\right)=\overrightarrow{DF}$ có độ dài bằng 2 lần vectơ $\left(-\overrightarrow{a}\right)$ và cùng hướng với vectơ $\left(-\overrightarrow{a}\right)$

Lý thuyết Tích của một số với một vectơ và các tính chất

Cho số k ≠ 0 và $\overrightarrow{a}\ne \overrightarrow{0}$. Tích của số k với $\overrightarrow{a}\ne \overrightarrow{0}$ là một vectơ, kí hiệu là $k\overrightarrow{a}$.

Vectơ $k\overrightarrow{a}$ cùng hướng với $\overrightarrow{a}$ nếu k > 0, ngược hướng với $\overrightarrow{a}$ nếu k < 0 và có độ dài bằng $\left|k\right|.\left|\overrightarrow{a}\right|$.

Ta quy ước $0\overrightarrow{a}=\overrightarrow{0}$ và $k\overrightarrow{0}=\overrightarrow{0}$.

Người ta còn gọi tích của một số với một vectơ là tích của một vectơ với một số.

Ví dụ: Cho tam giác ABC có D, E, F lần lượt là trung điểm các cạnh AB, BC, CA. Tìm các vectơ bằng: $2\overrightarrow{DE};-\frac{1}{2}\overrightarrow{CA};-2\overrightarrow{EC}$.

Hướng dẫn giải

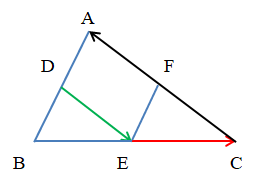
+ Vectơ bằng $2\overrightarrow{DE}$:

Tam giác ABC có D, E lần lượt là trung điểm của AB, BC.

Do đó DE là đường trung bình của tam giác ABC.

Suy ra DE // AC và 2DE = AC.

Vì k = 2 > 0 nên vectơ cần tìm cùng hướng với $\overrightarrow{DE}$ và có độ dài bằng 2DE.

Ta có $\overrightarrow{DE}$ cùng hướng với $\overrightarrow{AC}$ và 2DE = AC.

Do đó $2\overrightarrow{DE}=\overrightarrow{AC}$.

+ Vectơ bằng $-\frac{1}{2}\overrightarrow{CA}$:

Ta có F là trung điểm CA.

Do đó FA = CF = $\frac{1}{2}CA$.

Vì k = $-\frac{1}{2}$ < 0, nên vectơ cần tìm ngược hướng với $\overrightarrow{CA}$ và có độ dài bằng $\frac{1}{2}CA$.

Ta có $\overrightarrow{AF},\overrightarrow{FC}$ ngược hướng với $\overrightarrow{CA}$ và AF = FC = $\frac{1}{2}CA$.

Do đó $\overrightarrow{AF}=\overrightarrow{FC}=-\frac{1}{2}\overrightarrow{CA}$.

+ Vectơ bằng $-2\overrightarrow{EC}$:

Ta có E là trung điểm BC.

Do đó CB = 2EC.

Vì k = –2 < 0, nên vectơ cần tìm ngược hướng với $\overrightarrow{EC}$ và có độ dài bằng 2EC.

Ta có $\overrightarrow{CB}$ ngược hướng với $\overrightarrow{EC}$ và CB = 2EC.

Do đó $\overrightarrow{CB}=-2\overrightarrow{EC}$.

Tính chất:

 Với hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ bất kì, với mọi số thực h và k, ta có:

+) $k\left(\overrightarrow{a}+\overrightarrow{b}\right)=k\overrightarrow{a}+k\overrightarrow{b}$;

+) $\left(h+k\right)\overrightarrow{a}=h\overrightarrow{a}+k\overrightarrow{a}$;

+) $h\left(k\overrightarrow{a}\right)=\left(hk\right)\overrightarrow{a}$;

+) $1.\overrightarrow{a}=\overrightarrow{a}$;

+) $\left(-1\right).\overrightarrow{a}=-\overrightarrow{a}$.

Ví dụ: Ta có:

a) $6\left(\overrightarrow{x}+\overrightarrow{y}\right)=6\overrightarrow{x}+6\overrightarrow{y}$;

b) $\left(3+x\right)\overrightarrow{u}=3\overrightarrow{u}+x\overrightarrow{u}$;

c) $6.\left(-5\overrightarrow{i}\right)=\left[6.\left(-5\right)\right]\overrightarrow{i}=-30\overrightarrow{i}$;

d)  $2\overrightarrow{c}-7\overrightarrow{c}=\left(2-7\right)\overrightarrow{c}=-5\overrightarrow{c}$.

Ví dụ: Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$.

Hướng dẫn giải

Ta có $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$

$\iff \overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}=3\overrightarrow{MG}$       (quy tắc ba điểm)

$\iff 3\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=3\overrightarrow{MG}$

$\iff \overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$ 

⇔ G là trọng tâm của tam giác ABC (đpcm).

Xem thêm các bài giải Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Thực hành 1 trang 95 Toán lớp 10: Cho hai vectơ cho hai vectơ $\overrightarrow{a},\overrightarrow{b}$ và điểm M như hình 3...

Thực hành 2 trang 95 Toán lớp 10: Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$...

Vận dụng trang 95 Toán lớp 10: Một con tàu chở hàng A đang đi về hướng tây với tốc độ 20 hải lý/ giờ. Cùng lúc đó, một con tàu chở khách B đang đi về hướng đông với tốc độ 50 hải lý/giờ. Biểu diễn vectơ vận tốc $\overrightarrow{b}$ của tàu B theo vectơ vận tốc $\overrightarrow{a}$ của tòa A...

HĐ Khám phá 2 trang 96 Toán lớp 10: Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng phương khác $\overrightarrow{0}$ và cho $\overrightarrow{c}=\frac{\left|\overrightarrow{a}\right|}{\left|\overrightarrow{b}\right|}.\overrightarrow{b}$ . So sánh độ dài và hướng của hai vectơ $\overrightarrow{a}$ và $\overrightarrow{c}$...

Thực hành 3 trang 96 Toán lớp 10: Cho tứ giác ABCD có I và J lần lượt là trung điểm của AB và CD. Cho điểm G thỏa mãn $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$ . Chứng minh ba điểm I, G, J  thẳng hàng...

Bài 1 trang 97 Toán lớp 10: Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Với M là điểm tùy ý, chứng minh rằng:...

Bài 2 trang 97 Toán lớp 10: Cho tứ giác ABCD gọi M và N lần lượt là trung điểm của các cạnh AB và CD . Chứng minh rằng:...

Bài 3 trang 97 Toán lớp 10: Cho hai điểm phân biệt A và B. Xác định điểm M sao cho $\overrightarrow{MA}+4\overrightarrow{MB}=\overrightarrow{0}$...

Bài 4 trang 97 Toán lớp 10: Cho tứ giác ABCD. Gọi E, F, G lần lượt là trung điểm của các đoạn thẳng AB, CD, EF. Lấy điểm M tùy ý, chứng minh rằng $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}=4\overrightarrow{MG}$...

Bài 5 trang 97 Toán lớp 10: Máy bay A  đang bay về hướng Đông Bắc với tốc độ 600 km/h. Cùng lúc đó, máy bay B đang bay về hướng Tây Nam với tốc độ 800 km/h. Biểu diễn vectơ vận tốc của máy bay B theo vectơ vận tốc  của máy bay A...

Bài 6 trang 97 Toán lớp 10: Cho 2 điểm phân biệt A và B...

Bài 7 trang 97 Toán lớp 10: Cho tam giác ABC...

Xem thêm các bài giải SGK Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Tổng và hiệu của hai vecto

Bài 3: Tích của một số với một vecto

Bài 4: Tích vô hướng của hai vecto

Bài tập cuối chương 5

Bài 1: Số gần đúng và sai số