Với giải sách bài tập Toán 7 Ôn tập chương 1 trang 20, 21 sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Ôn tập chương 1 trang 20, 21

A. Câu hỏi (trắc nghiệm)

Tìm câu trả lời đúng trong các đáp án đã cho:

Giải SBT Toán 7 trang 20 Tập 1

Câu hỏi 1 trang 20 sách bài tập Toán lớp 7 Tập 1:Số $-\frac{1}{7}$ là:

A. Số tự nhiên;

B. Số nguyên;

C. Số hữu tỉ dương;

D. Số hữu tỉ.

Lời giải:

Đáp án đúng là D

$-\frac{1}{7}$ là số hữu tỉ âm nên chỉ có đáp án D thỏa mãn.

Câu hỏi 2 trang 20 sách bài tập Toán lớp 7 Tập 1:Kết quả của phép nhân 4³.4⁹ là:

A. 4⁶;

B. 4¹⁰;

C. 16⁶;

D. 2²⁰.

Lời giải:

Đáp án đúng là C

4³.4⁹ = 4^{3 + 9} = 4¹² = 4^2.6 = (4²)⁶ = 16⁶

Câu hỏi 3 trang 20 sách bài tập Toán lớp 7 Tập 1:Số hữu tỉ $\frac{a}{b}$ với $a,b\in \mathbb{Z},b\ne 0$ là dương nếu:

A. a, b cùng dấu;

B. a, b khác dấu;

C. a = 0, b dương;

D. a, b là hai số tự nhiên.

Lời giải:

Đáp án đúng là A

Số hữu tỉ $\frac{a}{b}$ với $a,b\in \mathbb{Z},b\ne 0$ là dương nếu a, b cùng dấu.

Câu hỏi 4 trang 20 sách bài tập Toán lớp 7 Tập 1:Khẳng định nào sau đây là sai?

A. Mỗi số hữu tỉ đều được biểu diễn bởi một điểm trên trục số;

B. Trên trục số, số hữu tỉ âm nằm bên trái điểm biểu diễn số 0;

C. Trên trục số, số hữu tỉ dương nằm bên phải điểm biểu diễn số 0;

D. Hai số hữu tỉ không phải luôn so sánh được với nhau.

Lời giải:

Đáp án đúng là D

Hai số hữu tỉ luôn so sánh được với nhau.

Câu hỏi 5 trang 20 sách bài tập Toán lớp 7 Tập 1:Khẳng định nào sau đây là đúng?

A. Mọi số nguyên đều là số tự nhiên;

B. Mọi số hữu tỉ đều là số nguyên;

C. Mọi số nguyên đều là số hữu tỉ;

D. Mọi phân số đều là số nguyên.

Lời giải:

Đáp án đúng là C

A sai vì -7 là số nguyên nhưng không phải số tự nhiên;

B sai vì $-\frac{1}{7}$ không phải là số thực.

D sai vì $-\frac{1}{7}$ là phân số nhưng không phải là số nguyên.

B. Bài tập

Bài 1.32 trang 20 sách bài tập Toán lớp 7 Tập 1:Tính:

a) 5 – $\left(1+\frac{1}{3}\right):\left(1-\frac{1}{3}\right)$

b) $\left(1+\frac{2}{3}-\frac{5}{4}\right)-\left(1-\frac{5}{4}\right)+\left(2022-\frac{2}{3}\right)$

Lời giải:

a) 5 – $\left(1+\frac{1}{3}\right):\left(1-\frac{1}{3}\right)$

= 5 – $\left(\frac{3}{3}+\frac{1}{3}\right):\left(\frac{3}{3}-\frac{1}{3}\right)$

= 5 – $\frac{4}{3}:\frac{2}{3}$

= 5 – $\frac{4}{3}.\frac{3}{2}$

= 5 – 2

= 3

b) $\left(1+\frac{2}{3}-\frac{5}{4}\right)-\left(1-\frac{5}{4}\right)+\left(2022-\frac{2}{3}\right)$

= $1+\frac{2}{3}-\frac{5}{4}-1+\frac{5}{4}+2022-\frac{2}{3}$

= $\left(\frac{2}{3}-\frac{2}{3}\right)+\left(-\frac{5}{4}+\frac{5}{4}\right)+\left(1+2022\right)$

= 0 + 0 + 2023

= 2023

Giải SBT Toán 7 trang 21 Tập 1

Bài 1.33 trang 21 sách bài tập Toán lớp 7 Tập 1: Tìm x, biết:

a) 0,7².x = 0,49²

b) x : (-0,5)³ = (-0,5)².

Lời giải:

a) 0,7².x = 0,49²

x = 0,49² : 0,7²

x = (0,49 : 0,7)²

x = 0,7²

x = 0,49

Vậy x = 0,49.

b) x : (-0,5)³ = (-0,5)².

x = (-0,5)² . (-0,5)³

x = (-0,5)²⁺³

x = (-0,5)⁵

Vậy x = (-0,5)⁵

Bài 1.34 trang 21 sách bài tập Toán lớp 7 Tập 1:Cho $a\in \mathbb{Q}$ và a ≠0. Hãy viết a⁸ dưới dạng:

a) Tích của hai lũy thừa, trong đó có một thừa số là a³;

b) Lũy thừa của a²;

c) Thương của hai lũy thừa trong đó số bị chia là a¹⁰.

Lời giải:

a) Ta có:

a⁸ = a^{5 + 3} = a⁵.a³.

b) Ta có:

a⁸ = a^2.4 = (a²)⁴

c) a⁸ = a^{10 – 2} = a¹⁰ : a²

Bài 1.35 trang 21 sách bài tập Toán lớp 7 Tập 1: Bảng sau cho chúng ta đường kính xấp xỉ của một số hàn tinh.

(1 dặm xấp xỉ 1,60934 km)

Hỏi đường kính của hành tinh nào lớn nhất? Đường kính của hành tính nào nhỏ nhất?

Lời giải:

Ta có:

7,4975.10⁴ = 74,975.10³; 3,0603.10⁴ = 30,603.10³

Vì 88,846 > 74,975 > 7,926 > 4,222 > 3,0603 > 3,032

Nên 88,846. 10³ > 74,975. 10³ > 7,926. 10³ > 4,222. 10³ > 3,0603. 10³ > 3,032. 10³

Do đó, đường kính của Mộc tinh là lớn nhất, đường kính của Thủy tinh là bé nhất.

Bài 1.36 trang 21 sách bài tập Toán lớp 7 Tập 1:Để làm 24 cái bánh, cần $1\frac{3}{4}$ cốc bột mì. Bạn An muốn làm 8 cái bánh. Hỏi bạn An cần bao nhiêu cốc bột mì?

Lời giải:

Đổi $1\frac{3}{4}=\frac{7}{4}$

24 cái bánh gấp 8 cái bánh số lần là:

24 : 8 = 3 (lần)

Bạn An cần số cốc bột mì để làm 8 cái bánh là:

$\frac{7}{4} : 3=\frac{7}{12}$ (cốc bột mì)

Bài 1.37 trang 21 sách bài tập Toán lớp 7 Tập 1: Biết 1² + 2² + 3² + … + 8² + 9² = 285.

Tính một cách hợp lí giá trị của biểu thức:

2² + 4² + 6² + … + 16² + 18².

Lời giải:

2² + 4² + 6² + … + 16² + 18².

= (1.2)² + (2.2)² + (2.3)² + (2.4)² + …+ (2.8)² + (2.9)²

= 1².2² + 2².2² + 2².3² + 2².4² + … + 2².8² + 2².9²

= 2².( 1² + 2² + 3² + … + 8² + 9²)

= 4.285 = 1140.

Bài 1.38 trang 21 sách bài tập Toán lớp 7 Tập 1:Tính giá trị của biểu thức: $A=\frac{{25}^6+5^4}{{25}^5+25}$.

Lời giải:

$A=\frac{{25}^6+5^4}{{25}^5+25}$

$A=\frac{{\left(5^2\right)}^6+5^4}{{\left(5^2\right)}^5+5^2}$

$A=\frac{5^{12}+5^4}{5^{10}+5^2}$

$A=\frac{5^{8+4}+5^4}{5^{8+2}+5^2}$

$A=\frac{5^8{.5}^4+5^4}{5^8{.5}^2+5^2}$

$A=\frac{5^4.\left(5^8+1\right)}{5^2.\left(5^8+1\right)}$

A = $\frac{5^4}{5^2}=5^2$.

Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 4: Thứ tự thực hiện các phép tính. Quy tắc chuyển vế

SBT Toán 7: Ôn tập chương 1

Bài 5: Làm quen với số thập phân vô hạn tuần hoàn

Bài 6: Số vô tỉ. Căn bậc hai số học

Bài 7: Tập hợp các số thực

Lý thuyết Chương 1: Số hữu tỉ

1. Khái niệm số hữu tỉ và biểu diễn số hữu tỉ trên trục số

• Số hữu tỉ là số viết được dưới dạng phân số $\frac{\mathrm{a}}{\mathrm{b}}$ với a, b ∈ $\mathrm{\mathbb{Z}}$, b ≠ 0.

Tập hợp các số hữu tỉ được kí hiệu là $\mathrm{\mathbb{Q}}$.

• Cách biểu diễn số hữu tỉ $\frac{\mathrm{a}}{\mathrm{b}}$ trên trục số:

 + Chia đoạn thẳng đơn vị thành b phần bằng nhau, lấy một đoạn làm đơn vị mới.

 + Điểm biểu diễn số hữu tỉ $\frac{\mathrm{a}}{\mathrm{b}}$ cách O một đoạn bằng a đơn vị mới và nằm trước O (nếu số hữu tỉ âm) hoặc nằm sau O (nếu số hữu tỉ dương).

Ví dụ 1:

+  Các số – 7; 0,3; – 2$\frac{3}{4}$ là các số hữu tỉ vì chúng viết được dưới dạng phân số: – 7 = $\frac{-7}{1}$; 0,3 = $\frac{3}{10}$; – 2$\frac{3}{4}$ = $\frac{-11}{4}$.

+ Biểu diễn số hữu tỉ $\frac{3}{2}$ trên trục số ta làm như sau:

Chia đoạn thẳng đơn vị thành 2 phần bằng nhau. Lấy một đoạn làm đơn vị mới (H.a).

Số hữu tỉ $\frac{3}{2}$ được biểu diễn bởi điểm N (nằm sau gốc O) và cách O một đoạn bằng 3 đơn vị mới (H.b)

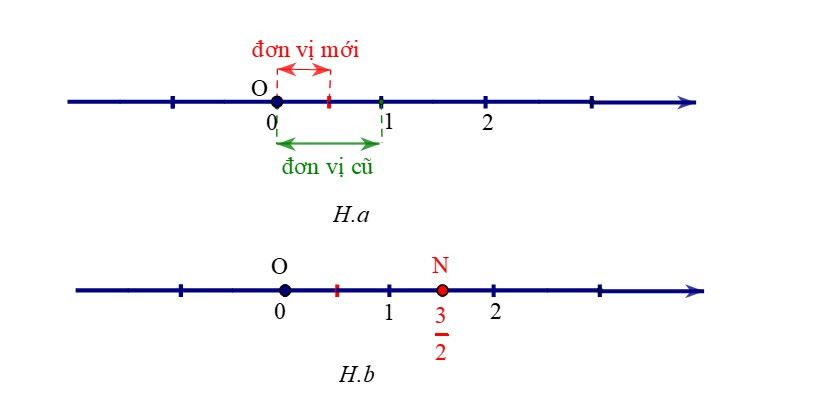
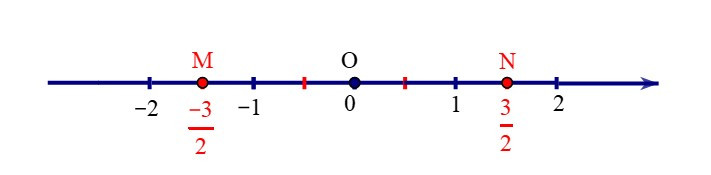
+ Số đối của số hữu tỉ $\frac{3}{2}$ là số hữu tỉ $-\frac{3}{2}$ được biểu diễn bởi điểm M (nằm trước gốc O). Ta có OM = ON.

Chú ý:

• Mỗi số hữu tỉ đều có một số đối. Số đối của số hữu tỉ m là số hữu tỉ – m.

• Số thập phân có thể viết dưới dạng phân số thập phân nên chúng đều là các số hữu tỉ. Tương tự, số nguyên, hỗn số cũng là các số hữu tỉ.

• Trên trục số, hai điểm biểu diễn của hai số hữu tỉ đối nhau nằm về hai phía khác nhau so với điểm O và có cùng khoảng cách đến O.

Ví dụ 2: Số đối của các số hữu tỉ sau: $-9,7;3\frac{5}{8};-\frac{1}{2};6.$

Hướng dẫn giải

Số đối của 0 – 9,7 là – (– 9,7) = 9,7;

Số đối của $3\frac{5}{8}$ là $-3\frac{5}{8}$;

Số đối của $-\frac{1}{2}$ là $-\left(-\frac{1}{2}\right)=\frac{1}{2}$;

Số đối của 6 là  – 6.

2. Thứ tự trong tập hợp các số hữu tỉ

• Ta có thể so sánh hai số hữu tỉ bất kì bằng cách viết chúng dưới dạng phân số rồi so sánh hai phân số đó.

• Với hai số hữu tỉ a, b bất kì, ta luôn có hoặc a = b hoặc a < b hoặc a > b.

Cho ba số hữu tỉ a, b, c. Nếu a < b và b < c thì a < c (tính chất bắc cầu).

• Trên trục số, nếu a < b thì điểm a nằm trước điểm b.

Ví dụ:

+ So sánh 0,5 và $\frac{3}{4}$ ta làm như sau:

Ta có 0,5 = $\frac{5}{10}=\frac{1}{2}=\frac{2}{4}$  

Vì 2 < 3 nên $\frac{2}{4}$ < $\frac{3}{4}$ hay 0,5 < $\frac{3}{4}$.

+ 0,5 < $\frac{3}{4}$ nên 0,5 nằm trước $\frac{3}{4}$ trên trục số.

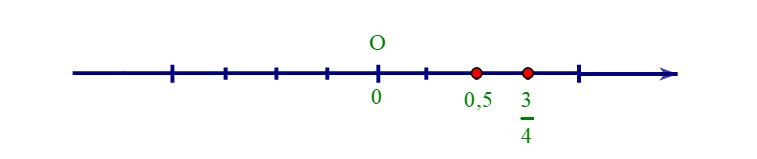
+ Ta có thể cử dụng tính chất bắc cầu để so sánh hai số hữu tỉ $\frac{5}{6}$ và $\frac{6}{5}$ như sau:

Vì $\frac{5}{6}<\frac{6}{6}=1$ và $1=\frac{5}{5}<\frac{6}{5}$ nên $\frac{5}{6}$ < 1 < $\frac{6}{5}$.

Vậy $\frac{5}{6}<\frac{6}{5}$.

Chú ý:

• Trên trục số, các điểm nằm trước gốc O biểu diễn số hữu tỉ âm (tức số hữu tỉ nhỏ hơn 0); các điểm nằm sau gốc O biểu diễn số hữu tỉ dương (tức số hữu tỉ lớn hơn 0). Số 0 không là số hữu tỉ dương, cũng không là số hữu tỉ âm.

3. Cộng và trừ hai số hữu tỉ

Mọi số hữu tỉ đều viết được dưới dạng phân số với mẫu dương nên ta có thể cộng, trừ hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc cộng, trừ phân số.

Ví dụ 1: Tính:

a) $\frac{-6}{18}+\frac{18}{27};$

b) – 0,32 + 0,98;

c) – 5 + $2\frac{1}{5}$.

Hướng dẫn giải

a) $\frac{-6}{18}+\frac{18}{27}=\frac{-1}{3}+\frac{2}{3}=\frac{-1+2}{3}=\frac{1}{3};$

b) – 0,32 + 0,98 = 0,98 – 0,32 = 0,66;

c) – 5 + $2\frac{1}{5}$ = $-\frac{25}{5}+\frac{11}{5}=\frac{-25+11}{5}=\frac{-14}{5}.$

Chú ý:

• Nếu hai số hữu tỉ đều được cho dưới dạng số thập phân thì ta có thể áp dụng quy tắc cộng và trừ đối với số thập phân.

• Trong phép cộng trừ với số hữu tỉ $\mathrm{\mathbb{Q}}$, ta có thể áp dụng các tính chất giao hoán, kết hợp, quy tắc dấu ngoặc như trong phép cộng trừ với số nguyên $\mathrm{\mathbb{Z}}$.

• Đối với một tổng trong $\mathrm{\mathbb{Q}}$, ta có thể đổi chỗ các số hạng, đặt dấu ngoặc để nhóm các số hạng một cách tùy ý như các tổng trong $\mathrm{\mathbb{Z}}$.

• Hai số đối nhau luôn có tổng bằng 0:

a + (– a) = 0.

Ví dụ 2: Thực hiện phép tính

a) $\frac{2}{-3}+\frac{-5}{6}+\frac{1}{3}+1\frac{1}{6}$;

b) $\frac{31}{3}-\frac{1}{2}-\left(\frac{2}{3}-\frac{1}{2}\right)$.

Hướng dẫn giải

a) $\frac{2}{-3}+\frac{-5}{6}+\frac{1}{3}+1\frac{1}{6}$

$=\frac{-2}{3}+\frac{-5}{6}+\frac{1}{3}+\frac{7}{6}$             (Viết số hữu tỉ dưới dạng phân số có mẫu dương)

$=\frac{-2}{3}+\frac{1}{3}+\frac{-5}{6}+\frac{7}{6}$             (Tính chất giao hoán)

$=\left(\frac{-2}{3}+\frac{1}{3}\right)+\left(\frac{-5}{6}+\frac{7}{6}\right)$      (Tính chất kết hợp)

$=\frac{-1}{3}+\frac{2}{6}$

$=\frac{-1}{3}+\frac{1}{3}=0$                       (Tổng hai số đối nhau bằng 0)

b)  $\frac{31}{3}-\frac{1}{2}-\left(\frac{2}{3}-\frac{1}{2}\right)$

$=\frac{31}{3}-\frac{1}{2}-\frac{2}{3}+\frac{1}{2}$                    (Quy tắc bỏ dấu ngoặc có dấu “–” đằng trước)

$=\left(\frac{31}{3}-\frac{2}{3}\right)+\left(-\frac{1}{2}+\frac{1}{2}\right)$         (Quy tắc đặt dấu ngoặc có dấu “+” đằng trước)

$=\frac{29}{3}+0=\frac{29}{3}$                       (Cộng với số 0)

4. Nhân và chia hai số hữu tỉ

• Ta có thể nhân, chia hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.

Chú ý:

• Phép nhân các số hữu tỉ cũng có các tính chất của phép nhân phân số.

• Nếu hai số hữu tỉ đều được cho dưới dạng số thập phân thì ta có thể áp dụng quy tắc nhân và chia đối với số thập phân.

Ví dụ 1: Tính:

a) $\frac{23}{3}\cdot \frac{6}{46}\cdot \left(-\frac{9}{10}\right)$;

b) $-\frac{7}{6}:1\frac{5}{7}$;

c) $\frac{7}{6}\cdot 3\frac{1}{4}+\frac{7}{6}\cdot \left(-0,25\right)$.

Hướng dẫn giải

a) $\frac{23}{3}\cdot \frac{6}{46}\cdot \left(-\frac{9}{10}\right)$

$=\frac{23}{3}\cdot \frac{3}{23}\cdot \left(-\frac{9}{10}\right)$

$=1\cdot \left(-\frac{9}{10}\right)=-\frac{9}{10}$                (Nhân với số 1)

b) $-\frac{7}{6}:1\frac{5}{7}$

$=-\frac{7}{6}:\frac{12}{7}$

$=-\frac{7}{6}\cdot \frac{7}{12}=-\frac{49}{72}$

c) $\frac{7}{6}\cdot 3\frac{1}{4}+\frac{7}{6}\cdot \left(-0,25\right)$

$=\frac{7}{6}\cdot \left[3\frac{1}{4}+\left(-0,25\right)\right]$

$=\frac{7}{6}\cdot \left(\frac{13}{4}+\frac{-1}{4}\right)$

$=\frac{7}{6}\cdot \frac{12}{4}=\frac{7}{2}$

Ví dụ 2: 1,25 . (– 4,6) = – (1,25 . 4,6) = – 5,75.

5. Lũy thừa với số mũ tự nhiên

• Lũy thừa bậc n của một số hữu tỉ x, kí hiệu xⁿ, là tích của n thừa số x (n là số tự nhiên lớn hơn 1)

${\mathrm{x}}^{\mathrm{n}}=\underset{\mathrm{n} \mathrm{thừa} \mathrm{số}}{\underbrace{\mathrm{x}\cdot \mathrm{x}\cdot \mathrm{x}\cdot ...\cdot \mathrm{x}}}$ (x $\in \mathrm{\mathbb{Q}}$, n $\in \mathrm{\mathbb{N}}$, n >1)

xⁿ đọc là x mũ n hoặc x lũy thừa n hoặc lũy thừa bậc n của x.

x gọi là cơ số, n gọi là số mũ.

Quy ước: x⁰ = 1 (x ≠ 0); x¹ = x.

Ví dụ:

+ 5³ đọc là 5 mũ 3 hoặc 5 lũy thừa 3 hoặc lũy thừa bậc 3 của 5.

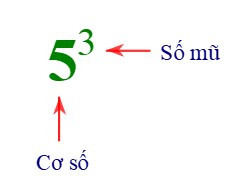
+  Tính ${\left(\frac{-1}{3}\right)}^4$

${\left(\frac{-1}{3}\right)}^4=\frac{-1}{3}\cdot \frac{-1}{3}\cdot \frac{-1}{3}\cdot \frac{-1}{3}=\frac{\left(-1\right)\cdot \left(-1\right)\cdot \left(-1\right)\cdot \left(-1\right)}{3\cdot 3\cdot 3\cdot 3}=\frac{1}{81}$

+ Tính và so sánh: $\frac{{12}^2}{6^2}$ và ${\left(-\frac{12}{6}\right)}^2$

$\frac{{12}^2}{6^2}=\frac{144}{36}=4$ và ${\left(-\frac{12}{6}\right)}^2={\left(-2\right)}^2=4$ nên $\frac{{12}^2}{6^2}={\left(-\frac{12}{6}\right)}^2$

Chú ý:

• Lũy thừa của một tích bằng tích các lũy thừa; lũy thừa của một thương bằng thương các lũy thừa.

${\left(\mathrm{x}\cdot \mathrm{y}\right)}^{\mathrm{n}}={\mathrm{x}}^{\mathrm{n}}\cdot {\mathrm{y}}^{\mathrm{n}}$;                               ${\left(\frac{\mathrm{x}}{\mathrm{y}}\right)}^{\mathrm{n}}=\frac{{\mathrm{x}}^{\mathrm{n}}}{{\mathrm{y}}^{\mathrm{n}}}$ (y ≠ 0).

Ví dụ:

${\left(\frac{3}{4}\right)}^{15}{.4}^{15}={\left(\frac{3}{4}.4\right)}^{15}=3^{15}$;

25³ : 5³ = ${\left(\frac{25}{5}\right)}^3=5^3=125$.

6. Nhân và chia hai lũy thừa cùng cơ số

• Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng hai số mũ.

${\mathrm{x}}^{\mathrm{m}}\cdot {\mathrm{x}}^{\mathrm{n}}={\mathrm{x}}^{\mathrm{m}+\mathrm{n}}$

• Khi chia hai lũy thừa cùng cơ số khác 0, ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ số mũ của lũy thừa chia.

${\mathrm{x}}^{\mathrm{m}}:{\mathrm{x}}^{\mathrm{n}}={\mathrm{x}}^{\mathrm{m}-\mathrm{n}}$ (x ≠ 0, m ≥ n)

Ví dụ:

+  Tính ${\left(\frac{2}{3}\right)}^2.{\left(\frac{2}{3}\right)}^5$

 ${\left(\frac{2}{3}\right)}^2.{\left(\frac{2}{3}\right)}^5={\left(\frac{2}{3}\right)}^{2+5}={\left(\frac{2}{3}\right)}^7=\frac{128}{2187}$

+  Tính ${\left(-9\right)}^5:{\left(-9\right)}^4$

${\left(-9\right)}^5:{\left(-9\right)}^4={\left(-9\right)}^{5-4}={\left(-9\right)}^1=-9$.

7. Lũy thừa của lũy thừa

• Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ.

${\left({\mathrm{x}}^{\mathrm{m}}\right)}^{\mathrm{n}}={\mathrm{x}}^{\mathrm{m}\cdot \mathrm{n}}$

Ví dụ:

+  Tính ${\left[{\left(-3\right)}^5\right]}^7$

 ${\left[{\left(-3\right)}^5\right]}^7={\left(-3\right)}^{5\cdot 7}={\left(-3\right)}^{35}$.

Mở rộng

• Lũy thừa với số mũ nguyên âm của một số khác 0.

${\mathrm{x}}^{-\mathrm{n}}=\frac{1}{{\mathrm{x}}^{\mathrm{n}}}$ với n là số nguyên dương, x ≠ 0.

Ví dụ: $\frac{1}{100}=\frac{1}{{10}^2}={10}^{-2}$

8. Thứ tự thực hiện các phép tính

• Với các biểu thức chỉ có phép cộng và phép trừ hoặc chỉ có phép nhân và phép chia ta thực hiện các phép tính theo thứ tự từ trái sang phải.

• Với các biểu thức không có dấu ngoặc, ta thực hiện theo thứ tự:

• Với các biểu thức có dấu ngoặc, ta thực hiện trong ngoặc trước, ngoài ngoặc sau.

$\left(\right)\to \left[\right]\to \left\{\right\}$

Ví dụ: Tính giá trị của biểu thức:

a) 1,5 – 2³ + 7,5 : 3;

b) $\frac{3}{2}:\left(\frac{1}{11}-\frac{5}{22}\right)+\frac{7}{4}\cdot \left(\frac{1}{14}-\frac{2}{7}\right)$.

Hướng dẫn giải:

a) 1,5 – 2³ + 7,5 : 3

= 1,5 – 8 + 2,5             (Thực hiện lũy thừa; nhân chia trước)

= – 6,5 + 2,5 = – 4

b) $\frac{3}{2}:\left(\frac{1}{11}-\frac{5}{22}\right)+\frac{7}{4}\cdot \left(\frac{1}{14}-\frac{2}{7}\right)$

$=\frac{3}{2}:\left(-\frac{3}{22}\right)+\frac{7}{4}\cdot \left(-\frac{3}{14}\right)$                (Thực hiện trong ngoặc trước)

$=\frac{3}{2}\cdot \left(-\frac{22}{3}\right)+\left(-\frac{3}{8}\right)$                       (Thực hiện nhân chia trước)

$=\left(-11\right)+\left(-\frac{3}{8}\right)=-\frac{91}{8}$.

9. Quy tắc chuyển vế

• Đẳng thức có dạng A = B. Trong đó A là vế trái; B là vế phải của đẳng thức.

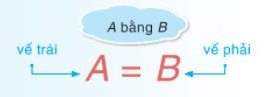
Ví dụ: 4,1 + x = 2,3 là một đẳng thức, trong đó 4,1 + x là vế trái, 2,3 là vế phải.

• Khi biến đổi các đẳng thức, ta thường áp dụng các tính chất sau:

   Nếu a = b thì:          b = a;         a + c = b + c.

• Quy tắc chuyển vế: Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” đổi thành dấu “–” và dấu “–” đổi thành dấu “+”.

+) Nếu a + b = c thì a = c – b;

+) Nếu a – b = c thì a = c + b.

Ví dụ: Tìm x, biết:

a) $\mathrm{x}+\frac{1}{3}=-\frac{5}{7}$;

b) $\mathrm{x}-\frac{5}{4}=\frac{9}{8}$.

Hướng dẫn giải

a) $\mathrm{x}+\frac{1}{3}=-\frac{5}{7}$

$\mathrm{x}=-\frac{5}{7}-\frac{1}{3}$       (Quy tắc chuyển vế)

$\mathrm{x}=-\frac{15}{21}-\frac{7}{21}$

$\mathrm{x}=-\frac{22}{21}$

Vậy $\mathrm{x}=-\frac{22}{21}$.

b) $\mathrm{x}-\frac{5}{4}=\frac{9}{8}$

$\mathrm{x}=\frac{9}{8}+\frac{5}{4}$                (Quy tắc chuyển vế)

$\mathrm{x}=\frac{9}{8}+\frac{10}{8}$

$\mathrm{x}=\frac{19}{8}$ 

Vậy $\mathrm{x}=\frac{19}{8}$.