Với giải sách bài tập Toán 7 Bài 3: Luỹ thừa với số mũ tự nhiên của một số hữu tỉ sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 3: Luỹ thừa với số mũ tự nhiên của một số hữu tỉ

Giải SBT Toán 7 trang 15 Tập 1

Bài 1.17 trang 15 sách bài tập Toán lớp 7 Tập 1:Đơn vị đo thời gian nhỏ nhất là yoctosecond (viết tắt là ys), nó bằng 0,000000000000000000000001 giây. Hãy viết số này dưới dạng lũy thừa của một số hữu tỉ.

Lời giải:

Nhận thấy phần thập phân của số này có 23 chữ số 0 và 1 chữ số 1 nên:

0,000000000000000000000001 = (0,1)²⁴

Bài 1.18 trang 15 sách bài tập Toán lớp 7 Tập 1: Viết các số sau dưới dạng lũy thừa của một số hữu tỉ.

a) 125 . 27;

b) 243 : 32.

Lời giải:

a) 125 . 27 = 5³.3³ = (5.3)³ = 15³;

b) 243 : 32. = 3⁵.2⁵ = (3.2)⁵ = 6⁵.

Bài 1.19 trang 15 sách bài tập Toán lớp 7 Tập 1:Đường kính của một tế bào hồng cầu là khoảng 7,4.${\left(\frac{1}{10}\right)}^4$cm. Hãy viết số này dưới dạng số thập phân.

Lời giải:

Ta có:

7,4.${\left(\frac{1}{10}\right)}^4$ = 7,4.$\frac{1^4}{{10}^4}$ = 7,4.$\frac{1}{10000}=\frac{1.7,4}{10000}$

$=\frac{74}{100000}=0,00074$

Vậy đường kính của một tế bào hồng cầu là khoảng 0,00074cm.

Bài 1.20 trang 15 sách bài tập Toán lớp 7 Tập 1: Tính giá trị của biểu thức:

a) ${\left(\frac{1}{2}\right)}^3.4+\frac{3}{4}$;

b) 4³ : 2⁵ + 3⁵ : 9².

Lời giải:

a) ${\left(\frac{1}{2}\right)}^3.4+\frac{3}{4}$

= $\frac{1^3}{2^3}.4+\frac{3}{4}$

= $\frac{1}{8}.4+\frac{3}{4}$

= $\frac{1}{2}+\frac{3}{4}$

= $\frac{2}{4}+\frac{3}{4}$

= $\frac{5}{4}$

b) 4³ : 2⁵ + 3⁵ : 9².

= (2²)³ : 2⁵ + 3⁵ : (3²)²

= 2⁶ : 2⁵ + 3⁵ : 3⁴

= 2 + 3 = 5

Bài 1.21 trang 15 sách bài tập Toán lớp 7 Tập 1:Bảng thống kê dưới đây ước lượng số dân của một số nước tại thời điểm năm 2020.

(theo cacnuoc.vn)

Em hãy sắp xếp tên các quốc gia theo thứ tự có số dân từ lớn đến bé.

Lời giải:

Ta có:

143,9.10⁷ = 1439.10⁶; 43,7.10⁴ = 0,437.10⁶; 13,8.10⁸ = 1380.10⁶

Vì 1439 > 1280 > 331 > 126,6 > 97,3 > 65,2 > 51,2 > 11,3 > 0,437

Nên 1439.10⁶ > 1280. 10⁶ > 331. 10⁶ > 126,6. 10⁶ > 97,3. 10⁶ > 65,2. 10⁶ > 51,2. 10⁶ > 11,3. 10⁶ > 0,437. 10⁶

Do đó sắp xếp tên các quốc gia theo thứ tự có dân số từ lớn đến bé là:

Trung quốc; Ấn Độ; Hoa Kỳ; Nhật Bản; Việt Nam; Pháp; Hàn Quốc; Cu Ba; Brunei.

Giải SBT Toán 7 trang 16 Tập 1

Bài 1.22 trang 16 sách bài tập Toán lớp 7 Tập 1: Thay dấu “?” bằng số thích hợp:

a) ${\left(\frac{2}{3}\right)}^5.{\left(\frac{2}{3}\right)}^{?}={\left(\frac{2}{3}\right)}^8$;

b) ${\left(\frac{-3}{4}\right)}^{?}:{\left(\frac{-3}{4}\right)}^7={\left(\frac{-3}{4}\right)}^2$

Lời giải:

a) ${\left(\frac{2}{3}\right)}^5.{\left(\frac{2}{3}\right)}^{?}={\left(\frac{2}{3}\right)}^8$

${\left(\frac{2}{3}\right)}^{?}={\left(\frac{2}{3}\right)}^8:{\left(\frac{2}{3}\right)}^5$

${\left(\frac{2}{3}\right)}^{?}={\left(\frac{2}{3}\right)}^{8-5}$

${\left(\frac{2}{3}\right)}^{?}={\left(\frac{2}{3}\right)}^3$

Vậy “?” là 3.

b) ${\left(\frac{-3}{4}\right)}^{?}:{\left(\frac{-3}{4}\right)}^7={\left(\frac{-3}{4}\right)}^2$

${\left(\frac{-3}{4}\right)}^{?}={\left(\frac{-3}{4}\right)}^2.{\left(\frac{-3}{4}\right)}^7$

${\left(\frac{-3}{4}\right)}^{?}={\left(\frac{-3}{4}\right)}^{2+7}$

${\left(\frac{-3}{4}\right)}^{?}={\left(\frac{-3}{4}\right)}^9$

Vậy “?” là 9

Bài 1.23 trang 16 sách bài tập Toán lớp 7 Tập 1: Không sử dụng máy tính cầm tay, hãy tính:

a) (-5)⁷, biết (-5)⁶ = 15 625;

b) 2¹², biết 2¹¹ = 2048.

Lời giải:

a) Ta có:

(-5)⁷ = (-5)⁶. (-5) = 15 625 . (-5) = -78 125;

b) Ta có:

2¹² = 2¹¹ . 2 = 2048 . 2 = 4096.

Bài 1.24 trang 16 sách bài tập Toán lớp 7 Tập 1:Hình vuông dưới đây có tính chất: Mỗi ô ghi một lũy thừa của 2, tích các số trong mỗi hàng, mỗi cột và mỗi đường chéo đều bằng nhau. Hãy điển các lũy thừa của 2 còn thiếu vào các ô trống.

Lời giải:

Ta thực hiện các phép nhân lũy thừa theo dàng ngang cột dọc đường chéo thu được kết quả trong bảng sau:

Bài 1.25 trang 16 sách bài tập Toán lớp 7 Tập 1: Tìm số tự nhiên n, biết:

a) 5ⁿ.${\left(\frac{1}{5}\right)}^3=125$;

b) 4.3ⁿ = 324.

Lời giải:

a) 5ⁿ.${\left(\frac{1}{5}\right)}^3=125$

5ⁿ.$\frac{1^3}{5^3}=125$

$\frac{5^n}{5^3}=5^3$

5^{n – 3} = 5³

n – 3 = 3

n = 3 + 3

n = 6

Vậy n = 6.

b) 4.3ⁿ = 324.

3ⁿ = 324 : 4

3ⁿ = 81

3ⁿ = 3⁴

n = 4

Vậy n = 4.

Bài 1.26 trang 16 sách bài tập Toán lớp 7 Tập 1:Tính $A=\frac{{27}^{10}+9^5}{9^{13}+{27}^2}$.

Lời giải:

$A=\frac{{27}^{10}+9^5}{9^{13}+{27}^2}$

$A=\frac{{\left(3^3\right)}^{10}+{\left(3^2\right)}^5}{{\left(3^2\right)}^{13}+{\left(3^3\right)}^2}$

$A=\frac{3^{30}+3^{10}}{3^{26}+3^6}$

$A=\frac{3^{20}{.3}^{10}+3^{10}}{3^{20}{.3}^6+3^6}$

$A=\frac{3^{10}.\left(3^{20}+1\right)}{3^6.\left(3^{20}+1\right)}$

$A=\frac{3^{10}}{3^6}=3^{10}:3^6=3^{10-6}=3^4$.

Xem thêm các bài giải SBT Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 2: Cộng, trừ, nhân, chia số hữu tỉ

Bài 3: Luỹ thừa với số mũ tự nhiên của một số hữu tỉ

Bài 4: Thứ tự thực hiện các phép tính. Quy tắc chuyển vế

SBT Toán 7: Ôn tập chương 1

Bài 5: Làm quen với số thập phân vô hạn tuần hoàn

Lý thuyết Lũy thừa với số mũ tự nhiên của một số hữu tỉ

1. Lũy thừa với số mũ tự nhiên

• Lũy thừa bậc n của một số hữu tỉ x, kí hiệu xⁿ, là tích của n thừa số x (n là số tự nhiên lớn hơn 1).

${\mathrm{x}}^{\mathrm{n}}=\underset{\mathrm{n} \mathrm{thừa} \mathrm{số}}{\underbrace{\mathrm{x}\cdot \mathrm{x}\cdot \mathrm{x}\cdot ...\cdot \mathrm{x}}}$  (x $\in \mathrm{\mathbb{Q}}$, n $\in \mathrm{\mathbb{N}}$, n >1)

xⁿ đọc là x mũ n hoặc x lũy thừa n hoặc lũy thừa bậc n của x.

x gọi là cơ số, n gọi là số mũ.

Quy ước: x⁰ = 1 (x ≠ 0); x¹ = x.

Ví dụ:

+ 5³ đọc là 5 mũ 3 hoặc 5 lũy thừa 3 hoặc lũy thừa bậc 3 của 5.

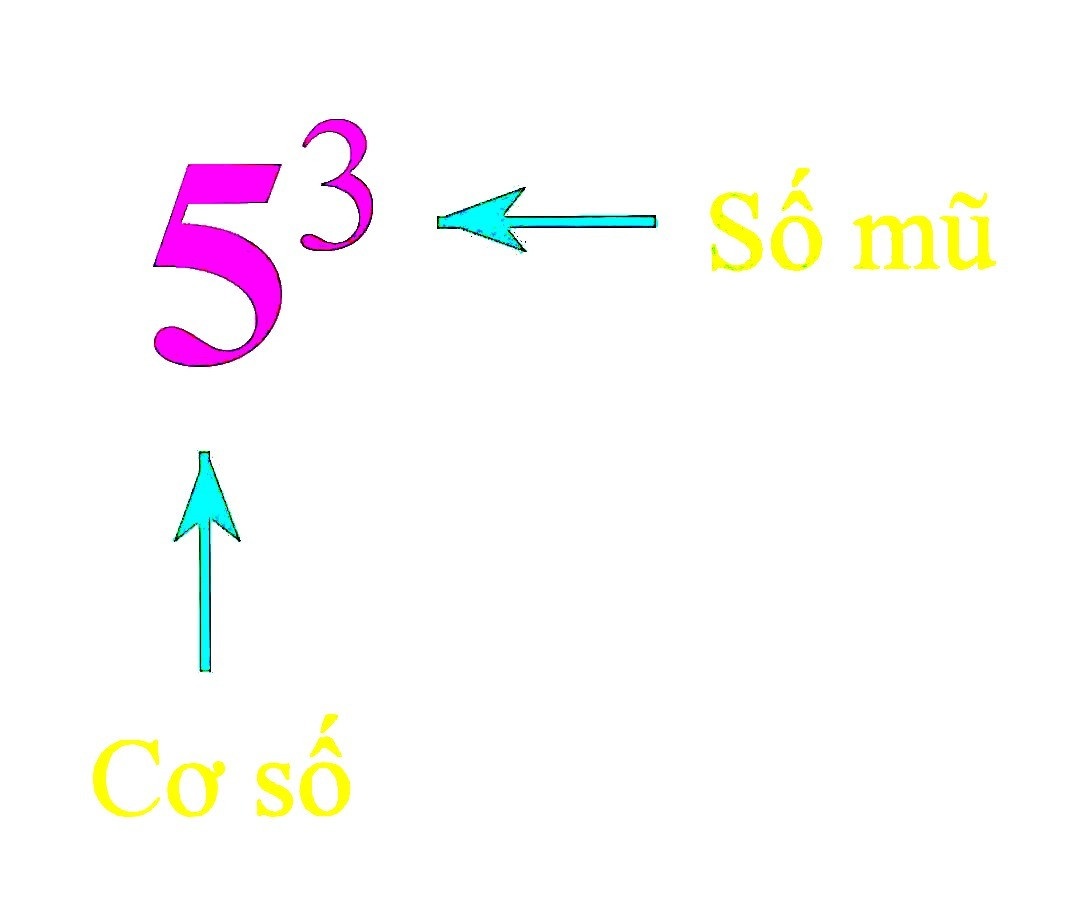
+  Tính ${\left(\frac{-1}{3}\right)}^4$

${\left(\frac{-1}{3}\right)}^4=\frac{-1}{3}\cdot \frac{-1}{3}\cdot \frac{-1}{3}\cdot \frac{-1}{3}=\frac{\left(-1\right)\cdot \left(-1\right)\cdot \left(-1\right)\cdot \left(-1\right)}{3\cdot 3\cdot 3\cdot 3}=\frac{1}{81}$

+ Tính và so sánh: $\frac{{12}^2}{6^2}$ và ${\left(-\frac{12}{6}\right)}^2$

$\frac{{12}^2}{6^2}=\frac{144}{36}=4$ và ${\left(-\frac{12}{6}\right)}^2={\left(-2\right)}^2=4$ nên $\frac{{12}^2}{6^2}={\left(-\frac{12}{6}\right)}^2$

Chú ý:

• Lũy thừa của một tích bằng tích các lũy thừa; lũy thừa của một thương bằng thương các lũy thừa.

${\left(\mathrm{x}\cdot \mathrm{y}\right)}^{\mathrm{n}}={\mathrm{x}}^{\mathrm{n}}\cdot {\mathrm{y}}^{\mathrm{n}}$;                               ${\left(\frac{\mathrm{x}}{\mathrm{y}}\right)}^{\mathrm{n}}=\frac{{\mathrm{x}}^{\mathrm{n}}}{{\mathrm{y}}^{\mathrm{n}}}$ (y ≠ 0).

Ví dụ:

${\left(\frac{3}{4}\right)}^{15}.4^{15}={\left(\frac{3}{4}.4\right)}^{15}=3^{15}$;

25³ : 5³ = ${\left(\frac{25}{5}\right)}^3=5^3=125$.

2. Nhân và chia hai lũy thừa cùng cơ số

• Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng hai số mũ.

${\mathrm{x}}^{\mathrm{m}}\cdot {\mathrm{x}}^{\mathrm{n}}={\mathrm{x}}^{\mathrm{m}+\mathrm{n}}$

• Khi chia hai lũy thừa cùng cơ số khác 0, ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ số mũ của lũy thừa chia.

${\mathrm{x}}^{\mathrm{m}}:{\mathrm{x}}^{\mathrm{n}}={\mathrm{x}}^{\mathrm{m}-\mathrm{n}}$ (x ≠ 0, m ≥ n)

Ví dụ: Tính:

a) ${\left(\frac{2}{3}\right)}^2.{\left(\frac{2}{3}\right)}^5$;

b) Tính ${\left(-9\right)}^5:{\left(-9\right)}^4$.

Hướng dẫn giải

a) ${\left(\frac{2}{3}\right)}^2.{\left(\frac{2}{3}\right)}^5={\left(\frac{2}{3}\right)}^{2+5}={\left(\frac{2}{3}\right)}^7=\frac{128}{2187}$;

b) ${\left(-9\right)}^5:{\left(-9\right)}^4={\left(-9\right)}^{5-4}={\left(-9\right)}^1=-9$.

3. Lũy thừa của lũy thừa

• Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ.

${\left({\mathrm{x}}^{\mathrm{m}}\right)}^{\mathrm{n}}={\mathrm{x}}^{\mathrm{m}\cdot \mathrm{n}}$

Ví dụ: Tính ${\left[{\left(-3\right)}^5\right]}^7$

Ta có: ${\left[{\left(-3\right)}^5\right]}^7={\left(-3\right)}^{5\cdot 7}={\left(-3\right)}^{35}$.

Mở rộng

• Lũy thừa với số mũ nguyên âm của một số khác 0.

${\mathrm{x}}^{-\mathrm{n}}=\frac{1}{{\mathrm{x}}^{\mathrm{n}}}$ với n là số nguyên dương, x ≠ 0.

Ví dụ: $\frac{1}{100}=\frac{1}{{10}^2}={10}^{-2}$