Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 11 Bài 16: Giới hạn của hàm số chi tiết sách Toán 11 Tập 1 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11. Mời các bạn đón xem:
Giải bài tập Toán lớp 11 Bài 16: Giới hạn của hàm số
,
trong đó m0 là khối lượng của vật khi nó đứng yên, c là vận tốc ánh sáng. Chuyện gì xảy ra với khối lượng của vật khi vận tốc của vật gần với vận tốc ánh sáng?
Lời giải:
Sau bài học này ta sẽ giải quyết được bài toán trên như sau:
Từ công thức khối lượng
ta thấy m là một hàm số của v, với tập xác định là nửa khoảng [0; c). Rõ ràng khi v tiến gần tới vận tốc ánh sáng, tức là v ⟶ c, ta có . Do đó , nghĩa là khối lượng m của vật trở nên vô cùng lớn khi vận tốc của vật gần tới vận tốc ánh sáng.
1. Giới hạn hữu hạn của một hàm số tại một điểm
HĐ1 trang 111 Toán 11 Tập 1: Nhận biết khái niệm giới hạn tại một điểm
Cho hàm số .
a) Tìm tập xác định của hàm số f(x).
b) Cho dãy số . Rút gọn f(xn) và tính giới hạn của dãy (un) với un = f(xn).
c) Với dãy số (xn) bất kì sao cho xn ≠ 2 và xn ⟶ 2, tính f(xn) và tìm .
Lời giải:
a) Biểu thức f(x) có nghĩa khi x – 2 ≠ 0 ⇔ x ≠ 2.
Do đó, tập xác định của hàm số f(x) là D = ℝ \ {2}.
b) Ta có:
.
.
c) Ta có: .
Vì xn ≠ 2 và xn ⟶ 2 với mọi n nên .
Do đó, .
Luyện tập 1 trang 113 Toán 11 Tập 1: Tính .
Lời giải:
Do mẫu thức có giới hạn là 0 khi x ⟶ 1 nên ta không thể áp dụng ngay quy tắc tính giới hạn của thương hai hàm số.
Lại có: .
Do đó .
HĐ2 trang 113 Toán 11 Tập 1: Nhận biết khái niệm giới hạn một bên
Cho hàm số 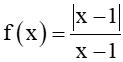
a) Cho và . Tính yn = f(xn) và y'n = f(x'n).
b) Tìm giới hạn của các dãy số (yn) và (y'n).
c) Cho các dãy số (xn) và (x'n) bất kì sao cho xn < 1 < x'n và xn ⟶ 1, x'n ⟶ 1, tính và .
Lời giải:
a) Ta có: với mọi n với mọi n.
Do đó,
Ta cũng có: với mọi n ⇒ x'n – 1 > 0 với mọi n.
Do đó,
b) Ta có ; .
c) Ta có:
Vì xn < 1 < x'n, suy ra xn – 1 < 0 và x'n – 1 > 0 với mọi n.
Do đó, f(xn) = – 1 và f(x'n) = 1.
Vậy = – 1 và = 1.
Luyện tập 2 trang 113 Toán 11 Tập 1: Cho hàm số
Tính , và .
Lời giải:
Với dãy số (xn) bất kì sao cho xn < 0 và xn ⟶ 0, ta có f(xn) = – xn.
Do đó .
Tương tự, với dãy số (xn) bất kì sao cho xn > 0 và xn ⟶ 0, ta có f(xn) = .
Do đó .
Khi đó, = = 0. Vậy = 0.
2. Giới hạn hữu hạn của hàm số tại vô cực
HĐ3 trang 114 Toán 11 Tập 1: Nhận biết khái niệm giới hạn tại vô cực
Cho hàm số có đồ thị như Hình 5.4.
Giả sử (xn) là dãy số sao cho xn > 1, xn ⟶ +∞. Tính f(xn) và tìm .
Lời giải:
Với (xn) là dãy số sao cho xn > 1, xn ⟶ +∞.
Ta có: .
Khi xn ⟶ +∞ thì .
Do đó .
Luyện tập 3 trang 115 Toán 11 Tập 1: Tính .
Lời giải:
Ta có
.
a) Tính h theo a.
b) Khi điểm A dịch chuyển về O, điểm H thay đổi thế nào? Tại sao?
c) Khi A dịch chuyển ra vô cực theo chiều dương của trục Ox, điểm H thay đổi thế nào? Tại sao?
Lời giải:
a) Ta có: A = (a; 0) ⇒ OA = a; B = (0; 1) ⇒ OB = 1
Tam giác OAB vuông tại O có đường cao OH nên ta có
Do đó, .
b) Khi điểm A dịch chuyển về O, ta có OA = a = 0, suy ra h = 0, do đó điểm H dịch chuyển về điểm O.
c) Khi A dịch chuyển ra vô cực theo chiều dương của trục Ox, ta có OA = a ⟶ +∞.
Ta có: .
Do đó, điểm H dịch chuyển về điểm B.
3. Giới hạn vô cực của một hàm số tại một điểm
HĐ4 trang 115 Toán 11 Tập 1: Nhận biết khái niệm giới hạn vô cực
Xét hàm số có đồ thị như Hình 5.6.
Cho , chứng tỏ rằng f(xn) ⟶ +∞.
Lời giải:
Ta có: , do đó .
Vì n ⟶ +∞ nên và f(xn) ⟶ +∞.
HĐ5 trang 116 Toán 11 Tập 1: Cho hàm số . Với các dãy số (xn) và (x'n) cho bởi , , tính và .
Lời giải:
Ta có: ;
.
Luyện tập 4 trang 116 Toán 11 Tập 1: Tính các giới hạn sau:
a) 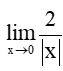
b) .
Lời giải:
a) Xét hàm số 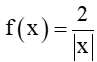
Do đó,
b) Đặt . Với mọi dãy số (xn) trong khoảng (– ∞; 2) mà , ta có
.
Do đó .
Luyện tập 5 trang 118 Toán 11 Tập 1: Tính và .
Lời giải:
+) Ta có: , x – 2 > 0 với mọi x > 2 và
.
Do đó, .
+) Ta có: , x – 2 < 0 với mọi x < 2 và
.
Do đó, .
Bài tập
Bài 5.7 trang 118 Toán 11 Tập 1: Cho hai hàm số và g(x) = x + 1. Khẳng định nào sau đây là đúng?
a) f(x) = g(x);
b) .
Lời giải:
+) Biểu thức f(x) có nghĩa khi x – 1 ≠ 0 ⇔ x ≠ 1.
Ta có: , với mọi x ≠ 1.
Biểu thức g(x) = x + 1 có nghĩa với mọi x.
Do đó, điều kiện xác định của hai hàm số f(x) và g(x) khác nhau, vậy khẳng định a) là sai.
+) Ta có: ;
.
Vậy nên khẳng định b) là đúng.
Bài 5.8 trang 118 Toán 11 Tập 1: Tính các giới hạn sau:
a) ;
b) .
Lời giải:
Do mẫu thức có giới hạn là 0 khi x ⟶ 0 nên ta không thể áp dụng ngay quy tắc tính giới hạn của thương hai hàm số đối với cả hai câu a và b.
a) Ta có:
Do đó .
b) Ta có: .
Do đó .
Tính và .
Lời giải:
Với dãy số (tn) bất kì sao cho tn < 0 và tn ⟶ 0, ta có H(tn) = 0.
Do đó .
Tương tự, với dãy số (tn) bất kì sao cho tn > 0 và tn ⟶ 0, ta có H(tn) = 1.
Do đó .
Bài 5.10 trang 118 Toán 11 Tập 1: Tính các giới hạn một bên:
a) ;
b) .
Lời giải:
a) Ta có: , x – 1 > 0 với mọi x > 1 và
.
Do đó, .
b) Ta có: , 4 – x > 0 với mọi x < 4 và
.
Do đó, .
Bài 5.11 trang 118 Toán 11 Tập 1: Cho hàm số 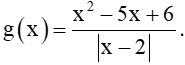
Tìm và .
Lời giải:
Ta có:
Do đó, ;
.
Bài 5.12 trang 118 Toán 11 Tập 1:Tính các giới hạn sau:
a) ;
b) .
Lời giải:
a) .
b) Ta có:
Do đó,
Bài 5.13 trang 118 Toán 11 Tập 1: Cho hàm số .
Tính và .
Lời giải:
Ta có:
+) và (do x – 2 > 0 khi x > 2).
Áp dụng quy tắc tìm giới hạn của tích, ta được .
+) và (do x – 2 < 0 khi x < 2).
Áp dụng quy tắc tìm giới hạn của tích, ta được .
Video bài giảng Toán 11 Bài 16: Giới hạn của hàm số - Kết nối tri thức
Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác:
Một vài áp dụng của toán học trong tài chính
Lý thuyết Giới hạn của hàm số
1. Giới hạn hữu hạn của hàm số tại một điểm
Giả sử (a;b) là một khoảng chứa điểm và hàm số xác định trên khoảng (a;b), có thể trừ điểm . Ta nói hàm số có giới hạn là số L khi dần tới nếu với dãy số bất kì, , và , ta có, kí hiệu hay , khi .
*Quy tắc tính giới hạn của hàm số tại một điểm
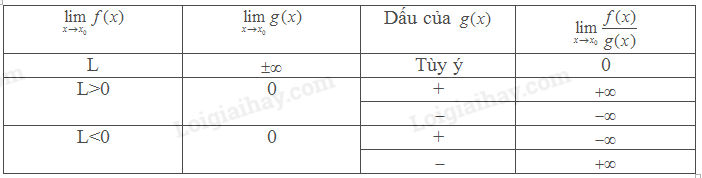
a, Nếu và thì
b, Nếu với mọi và thì và .
2. Giới hạn một bên
Cho hàm số xác định trên khoảng . Ta nói số L là giới hạn bên phải của khi nếu với dãy số bất kì thỏa mãn và ta có , kí hiệu .
Cho hàm số xác định trên khoảng . Ta nói số L là giới hạn bên trái của khi nếu với dãy số bất kì thỏa mãn và ta có , kí hiệu .
3. Giới hạn hữu hạn của hàm số tại vô cực
Cho hàm số xác định trên khoảng . Ta nói hàm số có giới hạn là số L khi nếu với dãy số bất kì và ta có , kí hiệu hay khi .
Cho hàm số xác định trên khoảng . Ta nói hàm số có giới hạn là số L khi nếu với dãy số bất kì và ta có , kí hiệu hay khi .
* Nhận xét:
Các quy tắc tính giới hạn hữu hạn tại một điểm cũng đúng cho giới hạn hữu hạn tại vô cực.
Với c là hằng số, , .
Với k là một số nguyên dương, ta có: .
4. Giới hạn vô cực của hàm số tại một điểm
a, Giới hạn vô cực
- Giả sử (a;b) là một khoảng chứa và hàm số xác định trên khoảng . Ta nói hàm số có giới hạn là khi dần tới nếu với dãy số bất kì, và , ta có, kí hiệu
Ta nói hàm số có giới hạn khi , kí hiệu , nếu .
- Cho hàm số xác định trên khoảng . Ta nói hàm số có giới hạn khi về bên phải nếu với dãy số bất kì thỏa mãn và ta có , kí hiệu .
Cho hàm số xác định trên khoảng . Ta nói hàm số có giới hạn khi về bên trái nếu với dãy số bất kì thỏa mãn và ta có , kí hiệu .
Các giới hạn một bên, được định nghĩa tương tự.
b, Một số quy tắc tính giới hạn vô cực
*Giới hạn của tích

*Giới hạn của thương