HĐ 3 trang 114 Toán 11 Tập 1 Kết nối tri thức | Giải bài tập Toán lớp 11

HĐ 3 trang 114 Toán 11 Tập 1 Kết nối tri thức | Giải bài tập Toán lớp 11

Van Anh Ngày: 11-08-2024 Lớp 11

452

Với giải HĐ 3 trang 114 Toán 11 Tập 1 Kết nối tri thức chi tiết trong Bài 16: Giới hạn của hàm số giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải bài tập Toán lớp 11 Bài 16: Giới hạn của hàm số

HĐ3 trang 114 Toán 11 Tập 1: Nhận biết khái niệm giới hạn tại vô cực

Cho hàm số $f (x) = 1 + \frac{2}{x - 1}$ có đồ thị như Hình 5.4.

HĐ3 trang 114 Toán 11 Tập 1 | Kết nối tri thức Giải Toán 11

Giả sử (x_n) là dãy số sao cho x_n > 1, x_n ⟶ +∞. Tính f(x_n) và tìm .

Lời giải:

Với (x_n) là dãy số sao cho x_n > 1, x_n ⟶ +∞.

Ta có: $f (x_{n}) = 1 + \frac{2}{x_{n} - 1}$ .

Khi x_n ⟶ +∞ thì $\lim_{n \to + \infty} \frac{2}{x_{n} - 1} = 0$ .

Do đó $\lim_{n \to + \infty} f (x_{n}) = \lim_{n \to + \infty} (1 + \frac{2}{x_{n} - 1}) = 1$ .

Lý thuyết Giới hạn hữu hạn của hàm số tại vô cực

Cho hàm số $y = f (x)$ xác định trên khoảng $(a; + \infty)$ . Ta nói hàm số $f (x)$ có giới hạn là số L khi $x \to + \infty$ nếu với dãy số $(x_{n})$ bất kì $x_{n} > a$ và $x_{n} \to + \infty$ ta có $f (x_{n}) \to L$ , kí hiệu $lim_{x \to + \infty} f (x) = L$ hay $f (x) \to L$ khi $x \to + \infty$ .

Cho hàm số $y = f (x)$ xác định trên khoảng $(- \infty; b)$ . Ta nói hàm số $f (x)$ có giới hạn là số L khi $x \to - \infty$ nếu với dãy số $(x_{n})$ bất kì $x_{n} < b$ và $x_{n} \to - \infty$ ta có $f (x_{n}) \to L$ , kí hiệu $lim_{x \to - \infty} f (x) = L$ hay $f (x) \to L$ khi $x \to - \infty$ .

* Nhận xét:

Các quy tắc tính giới hạn hữu hạn tại một điểm cũng đúng cho giới hạn hữu hạn tại vô cực.

Với c là hằng số, $lim_{x \to + \infty} c = c$ , $lim_{x \to - \infty} c = c$ .

Với k là một số nguyên dương, ta có: $lim_{x \to + \infty} (\frac{1}{x^{k}}) = 0, lim_{x \to - \infty} (\frac{1}{x^{k}}) = 0$ .

Video bài giảng Toán 11 Bài 16: Giới hạn của hàm số - Kết nối tri thức

Xem thêm các lời giải bài tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Mở đầu trang 111 Toán 11 Tập 1: Trong Thuyết tương đối của Einstein, khối lượng của vật chuyển động với vận tốc v cho bởi công thức...

HĐ1 trang 111 Toán 11 Tập 1: Nhận biết khái niệm giới hạn tại một điểm...

Luyện tập 1 trang 113 Toán 11 Tập 1: Tính $\lim_{x \to 1} \frac{x - 1}{\sqrt{x} - 1}$ ....

HĐ2 trang 113 Toán 11 Tập 1: Nhận biết khái niệm giới hạn một bên...

Luyện tập 2 trang 113 Toán 11 Tập 1: Cho hàm số ....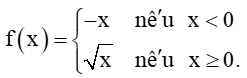

HĐ3 trang 114 Toán 11 Tập 1: Nhận biết khái niệm giới hạn tại vô cực....

Luyện tập 3 trang 115 Toán 11 Tập 1: Tính $\lim_{x \to + \infty} \frac{\sqrt{x^{2} + 2}}{x + 1}$ .....

Vận dụng trang 115 Toán 11 Tập 1: Cho tam giác OAB với A = (a; 0) và B = (0; 1) như Hình 5.5. Đường cao OH có độ dài là h.....

HĐ4 trang 115 Toán 11 Tập 1: Nhận biết khái niệm giới hạn vô cực....

HĐ5 trang 116 Toán 11 Tập 1: Cho hàm số $f (x) = \frac{1}{x - 1}$ . Với các dãy số (x_n) và (x'_n) cho bởi $x_{n} = 1 + \frac{1}{n}$ ,....

Luyện tập 4 trang 116 Toán 11 Tập 1: Tính các giới hạn sau:....

Luyện tập 5 trang 118 Toán 11 Tập 1: Tính $\lim_{x \to 2^{+}} \frac{2 x - 1}{x - 2}$ và $\lim_{x \to 2^{-}} \frac{2 x - 1}{x - 2}$ ......

Bài 5.7 trang 118 Toán 11 Tập 1: Cho hai hàm số $f (x) = \frac{x^{2} - 1}{x - 1}$ và g(x) = x + 1. Khẳng định nào sau đây là đúng?...

Bài 5.8 trang 118 Toán 11 Tập 1: Tính các giới hạn sau:....

Bài 5.9 trang 118 Toán 11 Tập 1: Cho hàm số (hàm H.eaviside, thường được dùng để mô tả việc chuyển trạng thái tắt/mở của dòng điện tại thời điểm t = 0).....

Bài 5.10 trang 118 Toán 11 Tập 1: Tính các giới hạn một bên:....

Bài 5.11 trang 118 Toán 11 Tập 1: Cho hàm số ......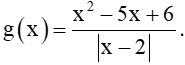

Bài 5.12 trang 118 Toán 11 Tập 1:Tính các giới hạn sau:....

Bài 5.13 trang 118 Toán 11 Tập 1: Cho hàm số $f (x) = \frac{2}{(x - 1) (x - 2)}$ .....

Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài 15: Giới hạn của dãy số

Bài 16: Giới hạn của hàm số

Bài 17: Hàm số liên tục

Bài tập cuối Chương 5

Một vài áp dụng của toán học trong tài chính

Từ khóa :

Toán 11

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

164

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15)

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

137

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

110

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.