Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 11 Giới hạn của hàm số, được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 11. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Giới hạn của hàm số. Mời các bạn đón xem:

Bài tập Toán 11 Giới hạn của hàm số

A. Bài tập Giới hạn của hàm số

Bài 1: Tính các giới hạn sau:

a) $\underset{x\to 3}{\lim }\frac{x^2+1}{2\sqrt{x}}$;

b) $\underset{x\to 1}{\lim }\frac{x^2+x-2}{x-1}$.

Hướng dẫn giải

a) 

$=\frac{3\cdot 3+1}{2\sqrt{3}}=\frac{5}{\sqrt{3}}$

b) Vì (x – 1) → 0 hay khi x → 1, nên ta chưa thể áp dụng ngay quy tắc tính giới hạn của hàm số tại một điểm.

Nhưng với x ≠ 1, ta có:

$\underset{x\to 1}{\lim }\frac{x^2+x-2}{x-1}$==$\underset{x\to 1}{\lim }$(x+2) = 3.

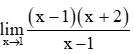
Bài 2: Tìm các giới hạn một bên:

a) $\underset{x\to 1^{+}}{\lim }\frac{x-3}{x-1}$;

b) $\underset{x\to 4^{-}}{\lim }\frac{x^2-2x+3}{4-x}$.

Hướng dẫn giải

a) Ta có: $\underset{x\to 1^{+}}{\lim }$(x-1) = 0 và x – 1 > 0 với mọi x > 1

$\underset{x\to 1^{+}}{\lim }$(x-3) = 1-3 = -2 <0

Do đó: $\underset{x\to 1^{+}}{\lim }\frac{x-3}{x-1}$ = – ∞.

b) Ta có: $\underset{x\to 4^{-}}{\lim }$(4-x) = 0 và 4 – x > 0 với mọi x < 4

$\underset{x\to 4^{-}}{\lim }$(x²-2x+3) = 4²-8+3 = 11 > 0

Do đó: $\underset{x\to 4^{-}}{\lim }\frac{x^2-2x+3}{4-x}$ = +∞.

Bài 3: Tính các giới hạn sau:

a) $\underset{x\to +\infty }{\lim }$(x³-2x);

b) $\underset{x\to -\infty }{\lim }$(x³-3x);

c) .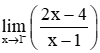

Hướng dẫn giải

a) 

b) 

c) Ta có: $\underset{x\to 1^{-}}{\lim }$(x-1) = 0 và x – 1 < 0 với mọi x < 1.

$\underset{x\to 1^{-}}{\lim }$(2x - 4) = 2.1 - 4 = -2<0.

Do đó, 

Bài 4: Cho hàm số f(x) = $\frac{2x^2-2}{x-1}$ và g(x) = x + 3. Khẳng định nào sau đây là sai?

a) f(x) = g(x).

b) $\underset{x\to 1}{\lim }\text{f(x)}=\underset{x\to 1}{\lim }\text{g(x)}$.

Hướng dẫn giải

a) Biểu thức f(x) có nghĩa khi x ≠ 1.

Ta có: f(x) = 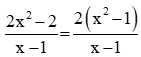 = 2(x+1) = 2x+2 với mọi x ≠ 1.

Biểu thức g(x) có nghĩa với mọi x.

Do đó f(x) ≠ g(x). Suy ra khẳng định a) là khẳng định sai.

b) $\underset{x\to 1}{\lim }$f(x) = $\underset{x\to 1}{\lim }$(2x+2) = 4

$\underset{x\to 1}{\lim }$g(x) = $\underset{x\to 1}{\lim }$(x+3) = 4

Vậy $\underset{x\to 1}{\lim }$f(x) = $\underset{x\to 1}{\lim }$g(x), do đó khẳng định b) là khẳng định đúng.

Bài 5. Tính các giới hạn sau:

a) $\underset{x\to 2}{\lim }\frac{\sqrt{4x-4}-x}{x^2-4}$ ;

b) $\underset{x\to 1}{\lim }\frac{\sqrt[3]{3x-2}-x}{\sqrt{3x+1}-2}$ .

Hướng dẫn giải

Bài 6. Tìm các giới hạn sau:

a) A = $\underset{x\to +\infty }{\lim }$x($\sqrt{4x^2+9}-2x$);

b) B = $\underset{x\to -\infty }{\lim }$($\sqrt{x^2-2x+2}-x$).

Hướng dẫn giải

$=\underset{x\to -\infty }{\lim }\frac{2+\frac{2}{-x}}{\sqrt{1-\frac{2}{x}+\frac{2}{x^2}}-1}=+\infty$

Bài 7. Chứng minh không tồn tại giới hạn của hàm số f(x) = $\sin \frac{1}{x}$ khi x tiến tới 0.

Hướng dẫn giải

Xét hai dãy số $x_n=\frac{1}{2n\pi };y_n=\frac{1}{\frac{\pi }{2}+2n\pi }$

Suy ra  $\lim x_n=\lim \frac{1}{2n\pi }=\frac{1}{2\pi }\lim \frac{1}{n}=\frac{1}{2\pi }.0=0$

Và $\lim y_n=\lim \frac{1}{\frac{\pi }{2}+2n\pi }=\frac{1}{\frac{\pi }{2}+2\pi \lim n}=0$

Khi đó ta xét:

• lim f($x_n$) = limsin ($2n\pi$) = 0;

• lim f ($y_n$) = limsin ($\frac{\pi }{2}+2n\pi$) = 1.

Do lim f($x_n$) $\ne$ lim f ($y_n$) (0 $\ne$ 1) nên hàm số f(x) = $\sin \frac{1}{x}$  không tồn tại giới hạn khi x tiến tới 0.

Bài 8. Cho f(x) =1 – x và g(x) = 2x³. Tính các giới hạn sau:

.

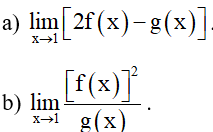
Hướng dẫn giải

.

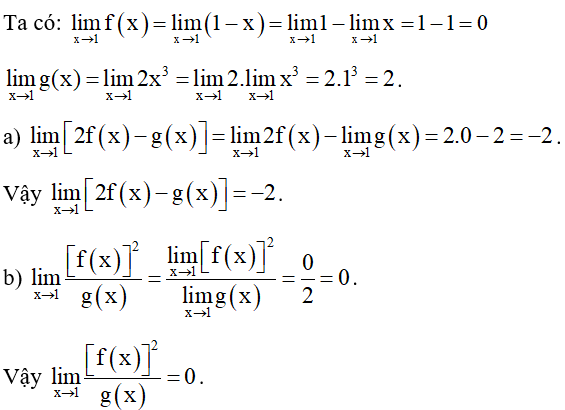
Bài 9. Sử dụng định nghĩa tìm giới hạn của hàm số:

a) $\underset{x\to 1}{\lim }{x}^3$;

b) $\underset{x\to -2}{\lim }\frac{4-x^2}{2+x}$.

Hướng dẫn giải

a) Giả sử (x_n) là một dãy bất kì và x_n → 1 khi n → +∞.

Khi đó $\mathrm{l}{\text{imx}}_n^3=1^3=1$.

Vậy $\underset{x\to 1}{\lim }{x}^3=1$.

b) Giả sử (x_n) là một dãy bất kì thỏa mãn x_n ≠ –2 và x_n → –2 khi n → +∞.

Vậy $\underset{x\to -2}{\lim }\frac{4-x^2}{2+x}=4$.

Bài 10. Tìm giới hạn của các hàm số sau:

a) ;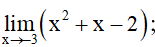

b) $\underset{x\to 1}{\lim }\frac{x^2+x-2}{x-1}$;

c) $\underset{x\to -\infty }{\lim }\frac{x+2}{x-1}$

Hướng dẫn giải

.

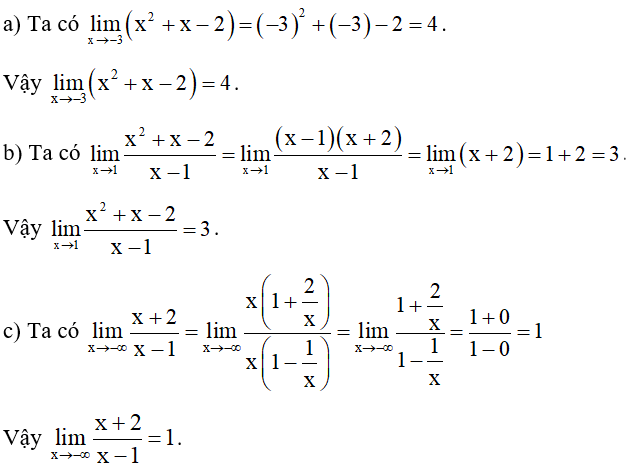
B. Lý thuyết Giới hạn của hàm số

1. Giới hạn hữu hạn của hàm số tại một điểm

Cho điểm x₀ thuộc K và hàm số y = f(x) xác định trên K hoặc K \ {x₀}.

Ta nói hàm số y = f(x) có giới hạn hữu hạn là số L khi x dần tới x₀ nếu với dãy số (x_n) bất kì, x_n ∈ K \ {x₀} và x_n → x₀, thì f(x_n) → L.

Kí hiệu:  hay f(x) → L khi x → x₀.

Ví dụ: Cho hàm số f(x) = $\frac{x^3-1}{x-1}$. Tìm $\underset{x\to 1}{\lim }f\left(x\right)$ .

Hướng dẫn giải

Hàm số y = f(x) xác định trên ℝ \ {1}.

Giả sử (x_n) là dãy số bất kì thỏa mãn x_n ≠ 1 với mọi n và x_n → 1 khi n → +∞.

Vậy $\underset{x\to 1}{\lim }f\left(x\right)=3$.

Nhận xét:

• $\underset{x\to x_0}{\lim }x=x_0$ ;

• $\underset{x\to x_0}{\lim }c=c$  (c là hằng số).

2. Các phép toán về giới hạn hữu hạn của hàm số

a) Cho $\underset{x\to x_0}{\lim }$f(x) = L và  $\underset{x\to x_0}{\lim }$g(x) = M. Khi đó:

• $\underset{x\to x_0}{\lim }$[ f(x) + g(x)] = L + M

• $\underset{x\to x_0}{\lim }$[ f(x) - g(x)] = L - M

• $\underset{x\to x_0}{\lim }$[ f(x) . g(x)] = L . M

b) Nếu f(x) ≥ 0 và $\underset{x\to x_0}{\lim }$f(x) = L thì L ≥ 0 và $\underset{x\to x_0}{\lim }\sqrt{f\left(\mathrm{(x)}\right)}=\sqrt{L}$

(Dấu của f (x) được xét trên khoảng tìm giới hạn, x ≠ x₀).

Nhận xét:

• $\underset{x\to x_0}{\lim }{x}^k=x_0^k$ , k là số nguyên dương;

• $\underset{x\to x_0}{\lim }$[cf(x) = c $\underset{x\to x_0}{\lim }$ f(x)  ( $c\in ℝ$, nếu tồn tại $\underset{x\to x_0}{\lim }$f(x) $\in \mathrm{ℝ}$) .

Ví dụ: Tìm các giới hạn sau:

a) $\underset{x\to -1}{\lim }2x^2+4x-5$ ;                          

b) $\underset{x\to 2}{\lim }\frac{\sqrt{2x+5}-3}{x-2}$ .

Hướng dẫn giải

a) $\underset{x\to -1}{\lim }2x^2+4x-5=\underset{x\to -1}{\lim }2x^2+\underset{x\to -1}{\lim }4x-\underset{x\to -1}{\lim }5$

$=2\underset{x\to -1}{\lim }{x}^2+4\underset{x\to -1}{\lim }x-\underset{x\to -1}{\lim }5=2.{\left(-1\right)}^2+4.\left(-1\right)-5=-7$.

b) $\underset{x\to 2}{\lim }\frac{\sqrt{2x+5}-3}{x-2}$

$=\underset{x\to 2}{\lim }\frac{2}{\sqrt{2x+5}+3}$

$=\frac{2}{\sqrt{2.2+5}+3}=\frac{1}{3}$.

3. Giới hạn một phía

Cho hàm số y = f(x) xác định trên khoảng (x₀; b).

• Ta nói hàm số y = f(x) có giới hạn bên phải là +∞ khi x → x₀ về bên phải nếu với dãy số (x_n) bất kì, x₀ < x_n < b và x_n → x₀, thì f(x_n) → +∞.

Kí hiệu: $\underset{x\to x_0^{+}}{\lim }$f(x) = +∞ hay f(x) → +∞ khi $x\to x_0^{+}$ .

• Ta nói hàm số y = f(x) có giới hạn bên phải là −∞ khi x → x₀ về bên phải nếu với dãy số (x_n) bất kì, x₀ < x_n < b và x → x₀, thì f(x_n) → −∞..

Kí hiệu: $\underset{x\to x_0^{+}}{\lim }$f(x) = −∞  hay f(x) → -∞  khi $x\to x_0^{+}$ .

Chú ý:

a) Các giới hạn  $\underset{x\to x_0^{-}}{\lim }$f(x) = +∞, $\underset{x\to x_0^{-}}{\lim }$ f(x) = -∞,  $\underset{x\to +\infty }{\lim }$f(x) = +∞, $\underset{x\to +\infty }{\lim }$f(x) = -∞, $\underset{x\to -\infty }{\lim }$f(x) = +∞,$\underset{x\to -\infty }{\lim }$f(x) = -∞ được định nghĩa tương tự như trên.

b) Ta có các giới hạn thường dùng sau:

• $\underset{x\to a^{+}}{\lim }\frac{1}{x-a}=+\infty$  và $\underset{x\to a^{-}}{\lim }\frac{1}{x-a}=-\infty \text{\hspace{0.33em}(}\left(a\in ℝ\right)$) ;

• $\underset{x\to +\infty }{\lim }{x}^k=+\infty$  với k là nguyên dương;

• $\underset{x\to -\infty }{\lim }{x}^k=+\infty$  nếu k là số nguyên dương chẵn;

• $\underset{x\to -\infty }{\lim }{x}^k=-\infty$  nếu k là số nguyên dương lẻ.

c) Các phép toán trên giới hạn hàm số của Mục 2 chỉ áp dụng được khi tất cả các hàm số được xét có giới hạn hữu hạn. Với giới hạn vô cực, ta có một số quy tắc sau đây.

Nếu $\underset{x\to x_0^{+}}{\lim }$f(x) = $L\ne 0$  và $\underset{x\to x_0^{+}}{\lim }$g(x) = +∞ (hoặc $\underset{x\to x_0^{+}}{\lim }$g(x) = -∞ )  thì $\underset{x\to x_0^{+}}{\lim }$[(f(x) . g(x)]  được tính theo quy tắc cho bởi bảng sau:

Các quy tắc trên vẫn đúng khi thay $x_0^{+}$  thành $x_0^{-}$  (hoặc +∞, −∞).

Ví dụ: Tìm các giới hạn sau:

a) $\underset{x\to -3^{+}}{\lim }\frac{2-3x}{x+3}$ ;

b) $\underset{x\to -\infty }{\lim }$($x^3+2$).

Hướng dẫn giải

Video bài giảng Toán 11 Bài 16: Giới hạn của hàm số - Kết nối tri thức