Với giải sách bài tập Toán 11 Bài 16: Giới hạn của hàm số sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán 11 Bài 16: Giới hạn của hàm số

Bài 5.11 trang 83 SBT Toán 11 Tập 1: Cho hàm số $f\left(x\right)=\left(\begin{array}{c}x neu x>1\\ 2 neu x=1\\ 1 neu x<1\end{array}\right)$ . Hàm số f(x) có giới hạn khi x → 1 không?

Lời giải:

Ta có $\underset{x\to 1^{+}}{\lim }f\left(x\right)=\underset{x\to 1^{+}}{\lim }x=1$ và $\underset{x\to 1^{-}}{\lim }f\left(x\right)=\underset{x\to 1^{-}}{\lim }1=1$ .

Vậy $\underset{x\to 1^{+}}{\lim }f\left(x\right)=\underset{x\to 1^{-}}{\lim }f\left(x\right)=1$ nên hàm số f(x) có giới hạn khi x → 1.

Bài 5.12 trang 83 SBT Toán 11 Tập 1: Tính các giới hạn sau:

a) $\underset{x\to 2}{\lim }\frac{\sqrt{4x+1}-3}{x-2}$ ;

b) $\underset{x\to 1}{\lim }\frac{x^3+x^2+x-3}{x^3-1}$ ;

c) $\underset{x\to 2^{+}}{\lim }\frac{x^2-5x+6}{{\left(x-2\right)}^2}$ ;

d) $\underset{x\to 0^{-}}{\lim }\frac{x^2+x-2}{x}$ .

Lời giải:

a)$\underset{x\to 2}{\lim }\frac{\sqrt{4x+1}-3}{x-2}$$=\underset{x\to 2}{\lim }\frac{4x+1-3^2}{\left(x-2\right)\left(\sqrt{4x+1}+3\right)}$

$=\underset{x\to 2}{\lim }\frac{4\left(x-2\right)}{\left(x-2\right)\left(\sqrt{4x+1}+3\right)}=\underset{x\to 2}{\lim }\frac{4}{\sqrt{4x+1}+3}=\frac{2}{3}$.

b)$\underset{x\to 1}{\lim }\frac{x^3+x^2+x-3}{x^3-1}$$=\underset{x\to 1}{\lim }\frac{\left(x^3-1\right)+\left(x^2-1\right)+\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}$

$=\underset{x\to 1}{\lim }\frac{\left(x-1\right)\left(\left(x^2+x+1\right)+\left(x+1\right)+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}$$=\underset{x\to 1}{\lim }\frac{x^2+2x+3}{x^2+x+1}=\frac{1+2+3}{1+1+1}=2$.

c) $\underset{x\to 2^{+}}{\lim }\frac{x^2-5x+6}{{\left(x-2\right)}^2}$$=\underset{x\to 2^{+}}{\lim }\frac{\left(x-2\right)\left(x-3\right)}{{\left(x-2\right)}^2}=\underset{x\to 2^{+}}{\lim }\frac{x-3}{x-2}$ .

Vì $\underset{x\to 2^{+}}{\lim }\left(x-2\right)=\mathrm{0,}\underset{x\to 2^{+}}{\lim }\left(x-3\right)=2-3=-1<0$ và x – 2 > 0 khi x → 2⁺, nên $\underset{x\to 2^{+}}{\lim }\frac{x-3}{x-2}=-\infty$.

Vậy $\underset{x\to 2^{+}}{\lim }\frac{x^2-5x+6}{{\left(x-2\right)}^2}=-\infty$ .

d)$\underset{x\to 0^{-}}{\lim }\frac{x^2+x-2}{x}$

Vì $\underset{x\to 0^{-}}{\lim }\left(x^2+x-2\right)=0+0-2=-2<0$ , $\underset{x\to 0^{-}}{\lim }x=0$ và x < 0 nên $\underset{x\to 0^{-}}{\lim }\frac{x^2+x-2}{x}=+\infty$ .

Bài 5.13 trang 83 SBT Toán 11 Tập 1: Tìm a để hàm số $f\left(x\right)=\left(\begin{array}{c}{x}^2+ax neu x>3\\ 3x^2+1 neu x\le 3\end{array}\right)$ có giới hạn khi x → 3.

Lời giải:

Ta có $\underset{x\to 3^{+}}{\lim }f\left(x\right)=\underset{x\to 3^{+}}{\lim }\left(x^2+ax\right)=3^2+3a=9+3a$ ;

$\underset{x\to 3^{-}}{\lim }f\left(x\right)=\underset{x\to 3^{-}}{\lim }\left(3x^2+1\right)={3.3}^2+1=28$.

Do đó, hàm số f(x) có giới hạn khi x → 3 khi $\underset{x\to 3^{+}}{\lim }f\left(x\right)=\underset{x\to 3^{-}}{\lim }f\left(x\right)$ , tức là 9 + 3a = 28.

Suy ra $a=\frac{19}{3}$.

Bài 5.14 trang 83 SBT Toán 11 Tập 1: Tìm các số thực a và b sao cho $\underset{x\to 1}{\lim }\frac{2x^2-ax+1}{x^2-3x+2}=b$ .

Lời giải:

Vì x = 1 là nghiệm của đa thức x² – 3x + 1 nên đa thức 2x² – ax + 1 phải có nghiệm x = 1. Khi đó, 2 . 1² – a . 1 + 1 = 0, suy ra a = 3.

Do đó,

 $$\begin{gathered} \underset{x\to 1}{\lim }\frac{2x^2-ax+1}{x^2-3x+2}=\underset{x\to 1}{\lim }\frac{2x^2-3x+1}{x^2-3x+2} \\ =\underset{x\to 1}{\lim }\frac{\left(2x-1\right)\left(x-1\right)}{\left(x-2\right)\left(x-1\right)} \end{gathered}$$

$=\underset{x\to 1}{\lim }\frac{2x-1}{x-2}=\frac{2.1-1}{1-2}=-1$.

Vậy b = – 1.

Bài 5.15 trang 83 SBT Toán 11 Tập 1: Cho hàm số $f\left(x\right)=\frac{\sqrt{x^2-x+2}}{x}$ . Tính:

a) $\underset{x\to +\infty }{\lim }f\left(x\right)$ ;

b) $\underset{x\to -\infty }{\lim }f\left(x\right)$ .

Lời giải:

a) $\underset{x\to +\infty }{\lim }f\left(x\right)$ = $\underset{x\to +\infty }{\lim }\frac{\sqrt{x^2-x+2}}{x}=\underset{x\to +\infty }{\lim }\frac{\sqrt{1-\frac{1}{x}+\frac{2}{x^2}}}{1}=1$ .

b) $\underset{x\to -\infty }{\lim }f\left(x\right)$ = $\underset{x\to -\infty }{\lim }\frac{\sqrt{x^2-x+2}}{x}=\underset{x\to -\infty }{\lim }\frac{-\sqrt{1-\frac{1}{x}+\frac{2}{x^2}}}{1}=-1$ .

Bài 5.16 trang 83 SBT Toán 11 Tập 1: Tính giới hạn $\underset{x\to +\infty }{\lim }\left(1-x\right)\left(1-x^2\right)\left(1-x^3\right)$ .

Lời giải:

Ta có $\underset{x\to +\infty }{\lim }\left(1-x\right)\left(1-x^2\right)\left(1-x^3\right)$

$=\underset{x\to +\infty }{\lim }x\left(\frac{1}{x}-1\right)x^2\left(\frac{1}{x^2}-1\right)x^3\left(\frac{1}{x^3}-1\right)$

$=\underset{x\to +\infty }{\lim }{x}^6\left(\frac{1}{x}-1\right)\left(\frac{1}{x^2}-1\right)\left(\frac{1}{x^3}-1\right)=-\infty$

Bài 5.17 trang 83 SBT Toán 11 Tập 1: Cho hàm số $g\left(x\right)=\sqrt{x^2+2x}-\sqrt{x^2-1}-2m$ với m là tham số. Biết $\underset{x\to +\infty }{\lim }g\left(x\right)=0$ , tìm giá trị của m.

Lời giải:

Ta có $g\left(x\right)=\sqrt{x^2+2x}-\sqrt{x^2-1}-2m$

$=\frac{x^2+2x-x^2+1}{\sqrt{x^2+2x}+\sqrt{x^2-1}}-2m$

$=\frac{2x+1}{\sqrt{x^2+2x}+\sqrt{x^2-1}}-2m$

$=\frac{2+\frac{1}{x}}{\sqrt{1+\frac{2}{x^2}}+\sqrt{1-\frac{1}{x^2}}}-2m$

Do đó, $\underset{x\to +\infty }{\lim }g\left(x\right)=\underset{x\to +\infty }{\lim }\left(\frac{2+\frac{1}{x}}{\sqrt{1+\frac{2}{x^2}}+\sqrt{1-\frac{1}{x^2}}}-2m\right)=\frac{2}{2}-2m=1-2m$ .

Mà $\underset{x\to +\infty }{\lim }g\left(x\right)=0$ nên 1 – 2m = 0, suy ra $m=\frac{1}{2}$ .

Bài 5.18 trang 83 SBT Toán 11 Tập 1: Cho m là một số thực. Biết $\underset{x\to -\infty }{\lim }\left(\left(m-x\right)\left(mx+1\right)\right)=-\infty$ . Xác định dấu của m.

Lời giải:

Ta có $\underset{x\to -\infty }{\lim }\left(\left(m-x\right)\left(mx+1\right)\right)=\underset{x\to -\infty }{\lim }\left(x^2\left(\frac{m}{x}-1\right)\left(m+\frac{1}{x}\right)\right)$ .

Vì $\underset{x\to -\infty }{\lim }\left(\frac{m}{x}-1\right)\left(m+\frac{1}{x}\right)=-m$ nên để $\underset{x\to -\infty }{\lim }\left(\left(m-x\right)\left(mx+1\right)\right)=-\infty$ thì – m < 0, có nghĩa là m > 0.

Vậy m > 0.

Bài 5.19 trang 83 SBT Toán 11 Tập 1: Cho hàm số $f\left(x\right)=\frac{{\sin }^{2}x}{x^2}$ . Chứng minh rằng $\underset{x\to +\infty }{\lim }f\left(x\right)=0$ .

Lời giải:

Lấy dãy số (x_n) bất kì sao cho x_n → +∞. Khi đó

$\left(f\left(x_n\right)\right)=\left(\frac{{\sin }^2{x}_n}{x_n^2}\right)=\frac{{\sin }^2{x}_n}{x_n^2}\le \frac{1}{x_n^2}\to 0$ khi n → +∞.

Vậy $\underset{n\to +\infty }{\lim }f\left(x_n\right)=0$. Từ đó suy ra $\underset{x\to +\infty }{\lim }f\left(x\right)=0$ .

Bài 5.20 trang 83 SBT Toán 11 Tập 1: Một đơn vị sản xuất hàng thủ công ước tính chi phí để sản xuất x đơn vị sản phẩm là C(x) = 2x + 55 (triệu đồng).

a) Tìm hàm số f(x) biểu thị chi phí trung bình để sản xuất mỗi đơn vị sản phẩm.

b) Tính $\underset{x\to +\infty }{\lim }f\left(x\right)$ . Giới hạn này có ý nghĩa gì?

Lời giải:

a) Chi phí trung bình để sản xuất mỗi đơn vị sản phẩm là

$f\left(x\right)=\frac{C\left(x\right)}{x}=\frac{2x+55}{x}$ (triệu đồng).

b) Ta có $\underset{x\to +\infty }{\lim }f\left(x\right)=\underset{x\to +\infty }{\lim }\frac{2x+55}{x}=\underset{x\to +\infty }{\lim }\frac{2+\frac{55}{x}}{1}=2$ .

Ý nghĩa của giới hạn trên: Khi số lượng sản phẩm sản xuất được càng lớn thì chi phí trung bình để sản xuất một đơn vị sản phẩm càng gần với 2 (triệu đồng).

Xem thêm các bài giải SBT Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 4

Bài 15: Giới hạn của dãy số

Bài 16: Giới hạn của hàm số

Bài 17: Hàm số liên tục

Bài tập cuối chương 5

Lý thuyết Giới hạn của hàm số

1. Giới hạn hữu hạn của hàm số tại một điểm

Giả sử (a;b) là một khoảng chứa điểm $x_0$và hàm số $y=f(x)$xác định trên khoảng (a;b), có thể trừ điểm $x_0$. Ta nói hàm số $f(x)$có giới hạn là số L khi $x$ dần tới $x_0$ nếu với dãy số $\left(x_n\right)$bất kì, $x_n\in \left(a;b\right)$,$x_n\ne x_0$ và $x_n\to x_0$, ta có$f(x_n)\to L$, kí hiệu $\underset{x\to x_0}{lim}f(x)=L$hay $f(x)\to L$, khi $x_n\to x_0$.

*Quy tắc tính giới hạn của hàm số tại một điểm

a, Nếu $\underset{x\to x_0}{lim}f(x)=L$và $\underset{x\to x_0}{lim}g(x)=M$thì

$\underset{x\to x_0}{lim}\left[f(x)\pm g(x)\right]=L\pm M$

$\underset{x\to x_0}{lim}\left[f(x).g(x)\right]=L.M$

$\underset{x\to x_0}{lim}\left[\frac{f(x)}{g(x)}\right]=\frac{L}{M}\left(M\ne 0\right)$

b, Nếu $f(x)\ge 0$với mọi $x\in \left(a;b\right)\mathrm{\setminus }\left\{x_0\right\}$ và $\underset{x\to x_0}{lim}f(x)=L$ thì $L\ge 0$và $\underset{x\to x_0}{lim}\sqrt{f(x)}=\sqrt{L}$.

2. Giới hạn một bên

Cho hàm số $y=f(x)$xác định trên khoảng $\left(x_0;b\right)$. Ta nói số L là giới hạn bên phải của $f(x)$khi $x\to x_0$ nếu với dãy số $\left(x_n\right)$bất kì thỏa mãn $x_0<x_n<b$ và $x_n\to x_0$ta có $f(x_n)\to L$, kí hiệu $\underset{x\to {x_0}^{+}}{lim}f(x)=L$.

Cho hàm số $y=f(x)$xác định trên khoảng $\left(a;x_0\right)$. Ta nói số L là giới hạn bên trái của khi $x\to x_0$ nếu với dãy số $\left(x_n\right)$bất kì thỏa mãn $a<x_n<x_0$ và $x_n\to x_0$ta có $f(x_n)\to L$, kí hiệu $\underset{x\to {x_0}^{-}}{lim}f(x)=L$.

3. Giới hạn hữu hạn của hàm số tại vô cực

Cho hàm số $y=f(x)$xác định trên khoảng $\left(a;+\mathrm{\infty }\right)$. Ta nói hàm số $f(x)$có giới hạn là số L khi $x\to +\mathrm{\infty }$ nếu với dãy số $\left(x_n\right)$bất kì $x_n>a$ và $x_n\to +\mathrm{\infty }$ta có $f(x_n)\to L$, kí hiệu $\underset{x\to +\mathrm{\infty }}{lim}f(x)=L$ hay $f(x)\to L$ khi $x\to +\mathrm{\infty }$.

Cho hàm số $y=f(x)$xác định trên khoảng $\left(-\mathrm{\infty };b\right)$. Ta nói hàm số $f(x)$có giới hạn là số L khi $x\to -\mathrm{\infty }$ nếu với dãy số $\left(x_n\right)$bất kì $x_n<b$ và $x_n\to -\mathrm{\infty }$ta có $f(x_n)\to L$, kí hiệu $\underset{x\to -\mathrm{\infty }}{lim}f(x)=L$ hay $f(x)\to L$ khi $x\to -\mathrm{\infty }$.

* Nhận xét:

Các quy tắc tính giới hạn hữu hạn tại một điểm cũng đúng cho giới hạn hữu hạn tại vô cực.

Với c là hằng số, $\underset{x\to +\mathrm{\infty }}{lim}c=c$, $\underset{x\to -\mathrm{\infty }}{lim}c=c$.

Với k là một số nguyên dương, ta có: $\underset{x\to +\mathrm{\infty }}{lim}(\frac{1}{x^k})=0,\underset{x\to -\mathrm{\infty }}{lim}(\frac{1}{x^k})=0$.

4. Giới hạn vô cực của hàm số tại một điểm

a, Giới hạn vô cực

- Giả sử (a;b) là một khoảng chứa $x_0$và hàm số $y=f(x)$xác định trên khoảng $\left(a;b\right)\mathrm{\setminus }\left\{x_0\right\}$. Ta nói hàm số $f(x)$có giới hạn là $+\mathrm{\infty }$khi $x$ dần tới $x_0$ nếu với dãy số $\left(x_n\right)$bất kì, $\left(a;b\right)\mathrm{\setminus }\left\{x_0\right\}$ và $x_n\to x_0$, ta có$f(x_n)\to +\mathrm{\infty }$, kí hiệu $\underset{x\to x_0}{lim}f(x)=+\mathrm{\infty }$

Ta nói hàm số $f(x)$có giới hạn $-\mathrm{\infty }$khi $x\to x_0$, kí hiệu $\underset{x\to x_0}{lim}f(x)=-\mathrm{\infty }$, nếu $\underset{x\to x_0}{lim}\left[-f(x)\right]=+\mathrm{\infty }$.

- Cho hàm số $y=f(x)$xác định trên khoảng $\left(x_0;b\right)$. Ta nói hàm số $f(x)$có giới hạn $+\mathrm{\infty }$ khi $x\to x_0$ về bên phải nếu với dãy số $\left(x_n\right)$bất kì thỏa mãn $x_0<x_n<b$ và $x_n\to x_0$ta có $f(x_n)\to +\mathrm{\infty }$, kí hiệu $\underset{x\to {x_0}^{+}}{lim}f(x)=+\mathrm{\infty }$.

Cho hàm số $y=f(x)$xác định trên khoảng $\left(a;x_0\right)$. Ta nói hàm số $f(x)$có giới hạn $+\mathrm{\infty }$ khi $x\to x_0$ về bên trái nếu với dãy số $\left(x_n\right)$bất kì thỏa mãn $a<x_n<x_0$ và $x_n\to x_0$ta có $f(x_n)\to +\mathrm{\infty }$, kí hiệu $\underset{x\to {x_0}^{-}}{lim}f(x)=+\mathrm{\infty }$.

Các giới hạn một bên$\underset{x\to {x_0}^{+}}{lim}f(x)=-\mathrm{\infty }$, $\underset{x\to {x_0}^{-}}{lim}f(x)=-\mathrm{\infty }$ được định nghĩa tương tự.

b, Một số quy tắc tính giới hạn vô cực

*Giới hạn của tích$\underset{x\to x_0}{lim}f(x).g(x)$

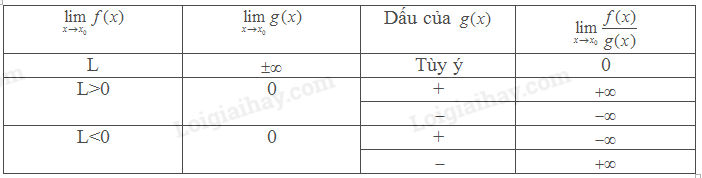
*Giới hạn của thương $\frac{f(x)}{g(x)}$