Với giải Hoạt động 3 trang 24 Toán 11 Tập 1 Cánh diều chi tiết trong Bài 3: Hàm số lượng giác và đồ thị giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải bài tập Toán lớp 11 Bài 3: Hàm số lượng giác và đồ thị

Hoạt động 3 trang 24 Toán 11 Tập 1: Với mỗi số thực x, tồn tại duy nhất điểm M trên đường tròn lượng giác sao cho (OA, OM) = x (rad) (Hình 22). Hãy xác định sinx.

Lời giải:

Giả sử tung độ của điểm M là y.

Khi đó ta có sinx = y.

 Lý thuyết Hàm số y = sinx

2.1. Định nghĩa

Quy tắc đặt tương ứng mỗi số thực x với một số thực sinx được gọi là hàm số y = sinx.

Tập xác định của hàm số y = sinx là ℝ.

2.2. Đồ thị của hàm số y = sinx

Ta có đồ thị của hàm số y = sinx trên ℝ được biểu diễn ở Hình 1:

2.3. Tính chất của hàm số y = sinx

Hàm số y = sinx có tập giá trị là [–1; 1] và có những tính chất sau:

⦁ Là hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O;

⦁ Là hàm số tuần hoàn chu kì 2π;

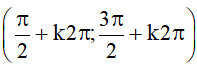
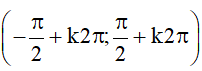
⦁ Là hàm số đồng biến trên mỗi khoảng , nghịch biến trên mỗi khoảng  với k ∈ ℤ.

Ví dụ 3.

+ Hàm số y = sinx đồng biến trên khoảng 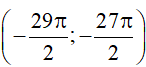 vì:

+ Hàm số y = sinx nghịch biến trên khoảng 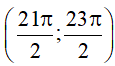 vì:

Nhận xét: Dựa vào đồ thị của hàm số y = sinx (Hình 1), ta thấy sinx = 0 tại những giá trị x = kπ (k ∈ ℤ). Vì vậy, tập hợp các số thực x sao cho sinx ≠ 0 là E = ℝ \ {kπ | k ∈ ℤ}.