Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 11 Bài 4: Phương trình lượng giác cơ bản chi tiết sách Toán 11 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 11. Mời các bạn đón xem:

Giải bài tập Toán lớp 11 Bài 4: Phương trình lượng giác cơ bản

Giải Toán 11 trang 32 Tập 1

Câu hỏi khởi động trang 32 Toán 11 Tập 1: Một vệ tinh nhân tạo bay quanh Trái Đất theo một quỹ đạo là đường elip (Hình 32). Độ cao h (km) của vệ tinh so với bề mặt Trái Đất được xác định bởi công thức h = 550 + 450cos$\frac{\pi }{50}$t (Nguồn: Đại số và Giải tích 11 Nâng cao, NXBGD Việt Nam, 2021), trong đó t là thời gian tính bằng phút kể từ lúc vệ tinh bay vào quỹ đạo. Tại thời điểm t bằng bao nhiêu thì vệ tinh cách mặt đất 1 000 km; 250 km; 100 km?

Trên thực tế, có nhiều bài toán dẫn đến việc giải một trong các phương trình có dạng: sinx = m, cosx = m, tanx = m, cotx = m, trong đó x là ẩn số, m là số thực cho trước. Các phương trình đó là các phương trình lượng giác cơ bản.

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

• Để vệ tinh cách mặt đất 1 000 km thì 550 + 450cos$\frac{\pi }{50}$t = 1 000

$\iff$450cos$\frac{\pi }{50}$t=450

$\iff$ cos$\frac{\pi }{50}$t = 1

$\iff$$\frac{\pi }{50}$t = k2$\pi$ (k$\in Z$, t$\ge$0)

$\iff$t = k2$\pi$.$\frac{50}{\pi }$ = 100k (k$\in Z${0; 1; 2; 3;...}

Vậy tại các thời điểm t = 100k (với k ∈ ℤ, t ≥ 0) (phút) kể từ lúc vệ tinh bay vào quỹ đạo thì vệ tinh cách mặt đất 1 000 km.

• Để vệ tinh cách mặt đất 250 km thì 550 + 450cos$\frac{\pi }{50}$t = 250

$\iff$ 450cos$\frac{\pi }{50}$t = -300

$\iff$ cos$\frac{\pi }{50}$t = -$\frac{2}{3}$

(Dùng máy tính cầm tay (chuyển về chế độ “radian”) bấm liên tiếp  ta được kết quả gần đúng là 2,3)

Vậy tại các thời điểm t $\approx \pm \frac{115}{\pi }$+100k (với k ∈ ℤ, t ≥ 0) (phút) kể từ lúc vệ tinh bay vào quỹ đạo thì vệ tinh cách mặt đất 250 km.

• Để vệ tinh cách mặt đất 100 km thì 550 + 450cos$\frac{\pi }{50}$t = 100

$\iff$ 450cos$\frac{\pi }{50}$t = -450

$\iff$ cos$\frac{\pi }{50}$t = -1

$\iff$$\frac{\pi }{50}$t = $\pi$+k2$\pi$ (k$\in$Z, t$\ge$0).

$\iff$ t = 50+100k (k$\in${0;1;2;3;...}

Vậy tại các thời điểm t = 50 + 100k (với k ∈ ℤ, t ≥ 0) (phút) kể từ lúc vệ tinh bay vào quỹ đạo thì vệ tinh cách mặt đất 100 km.

I. Phương trình tương đương

Hoạt động 1 trang 32 Toán 11 Tập 1: Cho hai phương trình (với cùng ẩn x):

x² ‒ 3x + 2 = 0 (1)

(x – 1)(x – 2) = 0 (2)

a) Tìm tập nghiệm S₁ của phương trình (1) và tập nghiệm S₂ của phương trình (2).

b) Hai tập S₁, S₂ có bằng nhau hay không?

Lời giải:

a) Ta có:

x² ‒ 3x + 2 = 0 (1)

Suy ra x = 1 hoặc x = 2.

Vậy phương trình (1) có tập nghiệm S₁ = {1; 2}.

(x – 1)(x – 2) = 0 (2)

Suy ra x = 1 hoặc x = 2.

Vậy phương trình (2) có tập nghiệm S₂ = {1; 2}.

b) Hai tập S₁, S₂ bằng nhau vì cùng là tập {1; 2}.

Luyện tập 1 trang 32 Toán 11 Tập 1: Hai phương trình x – 1 = 0 và $\frac{x^2-1}{x+1}$=0 có tương đương không? Vì sao?

Lời giải:

Tập nghiệm của phương trình x – 1 = 0 là S₁ = {1}.

Tập nghiệm của phương trình $\frac{x^2-1}{x+1}$ là S₂ = {1}.

Vì S₁ = S₂ nên hai phương trình x – 1 = 0 và $\frac{x^2-1}{x+1}$=0 tương đương.

Giải Toán 11 trang 33 Tập 1

Hoạt động 2 trang 33 Toán 11 Tập 1: Khẳng định 3x ‒ 6 = 0 $\iff$ 3x = 6 đúng hay sai?

Lời giải:

Phương trình 3x ‒ 6 = 0 có tập nghiệm S₁ = {2}.

Phương trình 3x = 6 có tập nghiệm S₂ = {2}.

Vì S₁ = S₂ nên hai phương trình 3x ‒ 6 = 0 và 3x = 6 tương đương

Khi đó ta viết 3x ‒ 6 = 0 $\iff$ 3x = 6.

Vậy khẳng định 3x ‒ 6 = 0 $\iff$ 3x = 6 là khẳng định đúng.

Luyện tập 2 trang 33 Toán 11 Tập 1: Giải phương trình: (x – 1)² = 5x – 11.

Lời giải:

Ta có: (x – 1)² = 5x – 11.

$\iff$ x² – 2x + 1 – (5x – 11) = 0

$\iff$ x² – 2x + 1 – 5x + 11 = 0

$\iff$ x² – 7x + 12 = 0

$\iff$ x = 3 hoặc x = 4.

Vậy tập nghiệm của phương trình đã cho là S = {3; 4}.

II. Phương trình sinx = m

Hoạt động 3 trang 33 Toán 11 Tập 1: a) Đường thẳng d: y = $\frac{1}{2}$ cắt đồ thị hàm số y = sinx, x ∈ [‒π; π] tại hai giao điểm A₀, B_0­ (Hình 33). Tìm hoành độ của hai giao điểm A₀, B_0­.

b) Đường thẳng d: y = $\frac{1}{2}$ cắt đồ thị hàm số y = sinx, x ∈ [π; 3π] tại hai giao điểm A₁, B_1­ (Hình 33). Tìm hoành độ của hai giao điểm A₁, B_1­.

Lời giải:

a) Với x ∈ [‒π; π] ta thấy sin x = $\frac{1}{2}$ tại x = $\frac{\pi }{6}$ và x = $\frac{5\pi }{6}$.

Do đó đường thẳng d: y = $\frac{1}{2}$ cắt đồ thị hàm số y = sinx, x ∈ [‒π; π] tại hai giao điểm A₀, B_0­ có hoành độ lần lượt là $x_{A_0}=\frac{\pi }{6}$ và $x_{B_0}=\frac{5\pi }{6}$.

b) Với x ∈ [π; 3π] ta thấy sin x = $\frac{1}{2}$ tại x = $\frac{13\pi }{6}$ và x = $\frac{17\pi }{6}$.

Do đó đường thẳng d: y = $\frac{1}{2}$ cắt đồ thị hàm số y = sinx, x ∈ [π; 3π] tại hai giao điểm A₁, B_1­ có hoành độ lần lượt là $x_{A_1}=\frac{13\pi }{6}$ và $x_{B_1}=\frac{17\pi }{6}$.

Giải Toán 11 trang 34 Tập 1

Luyện tập 3 trang 34 Toán 11 Tập 1: a) Giải phương trình: sin x = $\frac{\sqrt{3}}{2}$;

b) Tìm góc lượng giác x sao cho sinx = sin55°.

Lời giải:

a) Do sin x = $\frac{\sqrt{3}}{2}$ nên sin x = sin$\frac{\pi }{3}$

Vậy phương trình sin x = $\frac{\sqrt{3}}{2}$ có các nghiệm là x = $\frac{\pi }{3}$+k2$\pi$ và x = $\frac{2\pi }{3}$+k2$\pi$ với k ∈ ℤ.

b) sinx = sin55°

Vậy các góc lượng giác thỏa mãn sinx = sin55° là x = 55° + k360° và x = 125° + k360° với k ∈ ℤ.

Giải Toán 11 trang 35 Tập 1

Luyện tập 4 trang 35 Toán 11 Tập 1: Giải phương trình sin2x = sin$\left(x+\frac{\pi }{4}\right)$.

Lời giải:

Ta có:

sin2x = sin$\left(x+\frac{\pi }{4}\right)$

Vậy phương trình đã cho có các nghiệm là x = $\frac{\pi }{4}$+k2$\pi$ và x = $\frac{\pi }{4}$+k$\frac{2\pi }{3}$ với k ∈ ℤ.

III. Phương trình cosx = m

Hoạt động 4 trang 35 Toán 11 Tập 1: a) Đường thẳng d: y = $\frac{1}{2}$ cắt đồ thị hàm số y = cosx, x ∈ [‒π; π] tại hai giao điểm C₀, D_0­ (Hình 34). Tìm hoành độ của hai giao điểm C₀, D_0­.

b) Đường thẳng d: y = $\frac{1}{2}$ cắt đồ thị hàm số y = cosx, x ∈ [π; 3π] tại hai giao điểm C₁, D_1­ (Hình 34). Tìm hoành độ của hai giao điểm C₁, D_1­.

Lời giải:

a) Với x ∈ [‒π; π] ta thấy cosx = $\frac{1}{2}$ tại x = -$\frac{\pi }{3}$ và x = $\frac{\pi }{3}$.

Do đó đường thẳng d: y = $\frac{1}{2}$ cắt đồ thị hàm số y = cosx, x ∈ [‒π; π] tại hai giao điểm C₀, D_0­ có hoành độ lần lượt là $x_{C_0}=-\frac{\pi }{3}$ và $x_{D_0}=\frac{\pi }{3}$.

b) Với x ∈ [π; 3π] ta thấy cosx = $\frac{1}{2}$ tại x = $\frac{5\pi }{3}$ và x = $\frac{7\pi }{3}$.

Do đó đường thẳng d: y = $\frac{1}{2}$ cắt đồ thị hàm số y = cosx, x ∈ [π; 3π] tại hai giao điểm C₁, D_1­ có hoành độ lần lượt là $x_{C_1}=\frac{5\pi }{3}$ và $x_{D_1}=\frac{7\pi }{3}$.

Giải Toán 11 trang 36 Tập 1

Luyện tập 5 trang 36 Toán 11 Tập 1: a) Giải phương trình: cosx = -$\frac{1}{2}$.

b) Tìm góc lượng giác x sao cho cosx = cos(‒87°).

Lời giải:

a) Do cosx = -$\frac{1}{2}$ nên cosx = cos$\frac{2\pi }{3}$

Vậy phương trình đã cho có các nghiệm là x = $\frac{2\pi }{3}$+k2$\pi$ và x = -$\frac{2\pi }{3}$+k2$\pi$ với k ∈ ℤ.

b) cosx = cos(‒87°)

$\iff$ cosx = cos87°

Vậy các góc lượng giác x cần tìm là x = 87° + k360° và x = ‒87° + k360° với k ∈ ℤ.

Giải Toán 11 trang 37 Tập 1

Luyện tập 6 trang 37 Toán 11 Tập 1: Giải phương trình được nêu trong bài toán mở đầu.

Lời giải:

• Ta có:

550 + 450cos$\frac{\pi }{50}$t = 1 000

$\iff$450cos$\frac{\pi }{50}$t = 450

$\iff$ cos$\frac{\pi }{50}$t = 1

$\iff$ $\frac{\pi }{50}$t = k2$\pi$ (k$\in$Z, t$\ge$0)

$\iff$ t = k2$\pi$.$\frac{50}{\pi }$ = 100k (k$\in$Z, t$\ge$0).

Vậy phương trình này có các nghiệm là t = 100k với k ∈ ℤ, t ≥ 0.

• Ta có:

550 + 450cos$\frac{\pi }{50}$t = 250

$\iff$450cos$\frac{\pi }{50}$t = -300

$\iff$ cos$\frac{\pi }{50}$t = -$\frac{2}{3}$

(Dùng máy tính cầm tay (chuyển về chế độ “radian”) bấm liên tiếp  ta được kết quả gần đúng là 2,3)

Vậy phương trình có các nghiệm là t$\approx \frac{115}{\pi }$+100k và t$\approx -\frac{115}{\pi }$+100k với k ∈ ℤ, t ≥ 0.

• Ta có:

550 + 450cos$\frac{\pi }{50}$t = 100

$\iff$450cos$\frac{\pi }{50}$t = -450

$\iff$ cos$\frac{\pi }{50}$t = -1

$\iff$ $\frac{\pi }{50}$t = $\pi$ + k2$\pi$ (k$\in$Z, t$\ge$0)

$\iff$ t = 50 + 100k (k$\in$Z, t$\ge$0).

Vậy phương trình có các nghiệm là t = 50 + 100k với k ∈ ℤ, t ≥ 0.

IV. Phương trình tanx = m

Hoạt động 5 trang 37 Toán 11 Tập 1: Quan sát các giao điểm của đồ thị hàm số y = tanx và đường thẳng y = 1 (Hình 35).

a) Từ hoành độ giao điểm của đồ thị hàm số y = tanx và đường thẳng y = 1 trên khoảng $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$, hãy xác định tất cả các hoành độ giao điểm của hai đồ thị đó.

b) Có nhận xét gì về nghiệm của phương trình tanx = 1?

Lời giải:

a) Với x$\in \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ ta thấy tanx = 1 tại x=$\frac{\pi }{4}$.

Do đó đường thẳng y = 1 cắt đồ thị hàm số y = tanx trên khoảng $\in \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ tại điểm có hoành độ là $\frac{\pi }{4}$.

Do hàm số y = tanx tuần hoàn với chu kì là π nên đường thẳng y = 1 cắt đồ thị hàm số y = tanx tại các điểm có hoành độ là x = $\frac{\pi }{4}$+k$\pi$ (k$\in$Z).

b) Phương trình tanx = 1 có các nghiệm là x = $\frac{\pi }{4}$+k$\pi$ (k$\in$Z).

Luyện tập 7 trang 37 Toán 11 Tập 1: a) Giải phương trình: tanx = 1.

b) Tìm góc lượng giác x sao cho tanx = tan67°.

Lời giải:

a) Do tanx = 1 nên tanx = tan$\frac{\pi }{4}$ $\iff$x = $\frac{\pi }{4}$ (k$\in$Z).

Vậy phương trình tanx = 1 có các nghiệm là x=$\frac{\pi }{4}$ với k ∈ ℤ.

b) tanx = tan67° $\iff$ x = 67° + k180° (k ∈ ℤ).

Vậy các góc lượng giác x cần tìm là x = 67° + k180° với k ∈ ℤ.

V. Phương trình cotx = m

Giải Toán 11 trang 38 Tập 1

Hoạt động 6 trang 38 Toán 11 Tập 1: Quan sát các giao điểm của đồ thị hàm số y = cotx và đường thẳng y = ‒1 (Hình 36).

a) Từ hoành độ giao điểm của đồ thị hàm số y = cotx và đường thẳng y = ‒1 trên khoảng (0; π), hãy xác định tất cả các hoành độ giao điểm của hai đồ thị đó.

b) Có nhận xét gì về nghiệm của phương trình cotx = ‒1?

Lời giải:

a) Với x ∈ (0; π), ta thấy cotx = ‒1 tại x=$\frac{3\pi }{4}$.

Do đó đường thẳng y = ‒1 cắt đồ thị hàm số y = cotx trên khoảng (0; π) tại điểm có hoành độ là $\frac{3\pi }{4}$.

Do hàm số y = cotx tuần hoàn với chu kì là π nên đường thẳng y = ‒1 cắt đồ thị hàm số y = cotx tại các điểm có hoành độ là x=$\frac{3\pi }{4}$+k$\pi$ (k$\in$Z).

b) Phương trình cotx = ‒1 có các nghiệm là x=-$\frac{3\pi }{4}$+k$\pi$.

Giải Toán 11 trang 39 Tập 1

Luyện tập 8 trang 39 Toán 11 Tập 1: a) Giải phương trình: cotx = 1.

b) Tìm góc lượng giác x sao cho cotx = cot(‒83°).

Lời giải:

a) Do cotx = 1 nên cotx = cot$\frac{\pi }{4}$$\iff$ x=$\frac{\pi }{4}$+k$\pi$ (k$\in$Z).

Vậy phương trình cotx = 1 có các nghiệm là x=$\frac{\pi }{4}$+k$\pi$ với k ∈ ℤ.

b) cotx = cot(‒83°)

$\iff$ x = ‒83° + k180° (k ∈ ℤ).

Vậy các góc lượng giác x cần tìm là x = ‒83° + k180° với k ∈ ℤ.

VI. Giải phương trình lượng giác cơ bản bằng máy tính cầm tay

Luyện tập 9 trang 39 Toán 11 Tập 1: Sử dụng MTCT để giải mỗi phương trình sau với kết quả là radian (làm tròn kết quả đến hàng phần nghìn):

a) sinx = 0,2;

b) cosx = -$\frac{1}{5}$;

c) tanx = $\sqrt{2}$.

Lời giải:

Sau khi chuyển máy tính sang chế độ “radian”.

a) Bấm liên tiếp 

Ta được kết quả gần đúng là 0,201.

Vậy phương trình sinx = 0,2 có các nghiệm là:

x ≈ 0,201 + k2π, k ∈ ℤ

và x ≈ π – 0,201 + k2π, k ∈ ℤ.

b) Bấm liên tiếp 

Ta được kết quả gần đúng là 1,772.

Vậy phương trình cosx = -$\frac{1}{5}$ có các nghiệm là: x ≈ ± 1,772 + k2π, k ∈ ℤ.

c) Bấm liên tiếp 

Ta được kết quả gần đúng là 0,955.

Vậy phương trình tanx = $\sqrt{2}$ có các nghiệm là: x ≈ 0,955 + kπ, k ∈ ℤ.

Bài tập

Giải Toán 11 trang 40 Tập 1

Bài 1 trang 40 Toán 11 Tập 1: Giải phương trình:

a) sin$\left(2x-\frac{\pi }{3}\right)=-\frac{\sqrt{3}}{2}$;

b) sin$\left(3x+\frac{\pi }{4}\right)=-\frac{1}{2}$;

c) cos$\left(\frac{x}{2}+\frac{\pi }{4}\right)=\frac{\sqrt{3}}{2}$;

d) 2cos3x + 5 = 3;

e) 3tanx = -$\sqrt{3}$;

g) cotx - 3 = $\sqrt{3}$(1-cotx).

Lời giải:

a) sin$\left(2x-\frac{\pi }{3}\right)=-\frac{\sqrt{3}}{2}$

$\iff$sin$\left(2x-\frac{\pi }{3}\right)$ = sin$\left(-\frac{\pi }{3}\right)$

Vậy phương trình đã cho có các nghiệm là x=k$\pi$ và x=$\frac{5\pi }{6}$+k$\pi$ với k ∈ ℤ.

b) sin$\left(3x+\frac{\pi }{4}\right)=-\frac{1}{2}$

$\iff$ sin$\left(3x+\frac{\pi }{4}\right)$ = sin$\left(-\frac{\pi }{6}\right)$

Vậy phương trình đã cho có các nghiệm là x = $-\frac{5\pi }{36}+k\frac{2\pi }{3}$ và x = $\frac{11\pi }{36}+k\frac{2\pi }{3}$ với k ∈ ℤ.

c) cos$\left(\frac{x}{2}+\frac{\pi }{4}\right)=\frac{\sqrt{3}}{2}$

$\iff$cos$\left(\frac{x}{2}+\frac{\pi }{4}\right)$ = cos$\frac{\pi }{6}$

Vậy phương trình đã cho có các nghiệm là x = $-\frac{\pi }{6}$+k4$\pi$ và x=$-\frac{5\pi }{6}+k4\pi$ với k ∈ ℤ.

d) 2cos3x + 5 = 3

$\iff$ cos3x = ‒1

$\iff$ 3x = π + k2π (k ∈ ℤ)

$\iff$ x = $\frac{\pi }{3}$+k$\frac{2\pi }{3}$(k ∈ ℤ).

Vậy phương trình đã cho có các nghiệm là x = $\frac{\pi }{3}$+k$\frac{2\pi }{3}$ với k ∈ ℤ.

e) 3tanx = -$\sqrt{3}$

$\iff$ tanx = $-\frac{\sqrt{3}}{3}$

$\iff$ tanx = tan$\left(-\frac{\pi }{6}\right)$

$\iff$ x = $-\frac{\pi }{6}$ + k$\pi$ (k ∈ ℤ).

Vậy phương trình đã cho có các nghiệm là x = $-\frac{\pi }{6}$ + k$\pi$ với k ∈ ℤ.

g) cotx - 3 = $\sqrt{3}$(1-cotx)

$\iff$ cotx - 3 = $\sqrt{3}$-$\sqrt{3}$cotx

$\iff$ (1+$\sqrt{3}$)cotx = $\sqrt{3}$+3

$\iff$ cotx = $\frac{\sqrt{3}\left(1+\sqrt{3}\right)}{1+\sqrt{3}}$

$\iff$ cotx = $\sqrt{3}$

$\iff$ cotx = cot$\frac{\pi }{6}$

$\iff$ x = $\frac{\pi }{6}$+k$\pi$ (k ∈ ℤ).

Vậy phương trình đã cho có các nghiệm là x = $\frac{\pi }{6}$+k$\pi$ với k ∈ ℤ.

Bài 2 trang 40 Toán 11 Tập 1: Giải phương trình:

a) sin$\left(2x+\frac{\pi }{4}\right)$ = sinx;

b) sin2x = cos3x;

c) ${\cos }^{2}2x={\cos }^2\left(x+\frac{\pi }{6}\right)$ .

Lời giải:

a) sin$\left(2x+\frac{\pi }{4}\right)$ = sinx

Vậy phương trình đã cho có các nghiệm là x = $-\frac{\pi }{4}$+k2$\pi$ và x=$-\frac{\pi }{12}$+k$\frac{2\pi }{3}$ với k ∈ ℤ.

b) sin2x = cos3x

$\iff$cos$\left(\frac{\pi }{2}-2x\right)$ = cos3x

$\iff$ cos3x = cos$\left(\frac{\pi }{2}-2x\right)$

Vậy phương trình đã cho có các nghiệm là $x=\frac{\pi }{10}+k\frac{2\pi }{5}$ và $x=-\frac{\pi }{2}+k2\pi$ với k ∈ ℤ.

c) ${\cos }^{2}2x={\cos }^2\left(x+\frac{\pi }{6}\right)$

Vậy phương trình đã cho có các nghiệm là x = $\frac{\pi }{6}$+k$\pi$ và x = -$\frac{\pi }{18}$+k$\frac{\pi }{3}$ với k ∈ ℤ.

Bài 3 trang 40 Toán 11 Tập 1: Dùng đồ thị hàm số y = sinx, y = cosx để xác định số nghiệm của phương trình:

a) 3sinx + 2 = 0 trên khoảng $\left(-\frac{5\pi }{2};\frac{5\pi }{2}\right)$ ;

b) cosx = 0 trên đoạn  .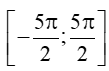

Lời giải:

a) Ta có: 3sinx + 2 = 0

$\iff$sinx = -$\frac{2}{3}$.

Đường thẳng y = -$\frac{2}{3}$ và đồ thị hàm số y = sinx trên khoảng $\left(-\frac{5\pi }{2};\frac{5\pi }{2}\right)$ được vẽ như sau:

Từ đồ thị, ta thấy đường thẳng y = -$\frac{2}{3}$ cắt đồ thị hàm số y = sinx trên khoảng $\left(-\frac{5\pi }{2};\frac{5\pi }{2}\right)$ tại 5 điểm A, B, C, D, E.

Vậy phương trình 3sinx + 2 = 0 có 5 nghiệm trên khoảng $\left(-\frac{5\pi }{2};\frac{5\pi }{2}\right)$.

b) Đường thẳng y = 0 (trục Ox) và đồ thị hàm số y = cosx trên đoạn 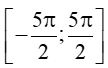 được vẽ như sau:

Từ đồ thị, ta thấy đường thẳng y = 0 cắt đồ thị hàm số y = cosx trên đoạn 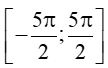 tại 6 điểm M, N, P, Q, I, K.

Vậy phương trình cosx = 0 có 6 nghiệm trên đoạn .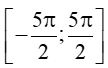

Bài 4 trang 40 Toán 11 Tập 1: Số giờ có ánh sáng mặt trời của một thành phố A ở vĩ độ 40° Bắc trong ngày thứ t của một năm không nhuận được cho bởi hàm số d(t) = 3sin$\left(\frac{\pi }{182}\left(t-80\right)\right)$+12 với t ∈ ℤ và 0 < t ≤ 365.

(Nguồn: Đại số và Giải tích 11 Nâng cao, NXBGD Việt Nam, 2020)

a) Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày nào trong năm?

b) Vào ngày nào trong năm thì thành phố A có đúng 9 giờ có ánh sáng mặt trời?

c) Vào ngày nào trong năm thì thành phố A có đúng 15 giờ có ánh sáng mặt trời?

Lời giải:

a) Để thành phố A có đúng 12 giờ có ánh sáng mặt trời thì:

3sin$\left(\frac{\pi }{182}\left(t-80\right)\right)$+12 = 12

$\iff$ sin$\left(\frac{\pi }{182}\left(t-80\right)\right)$ = 0

$\iff$ $\frac{\pi }{182}$(t-80) = k$\pi$ (k$\in$Z)

$\iff$ t - 80 = 182k (k$\in$Z)

$\iff$ t = 80+182k (k$\in$Z).

Do t ∈ ℤ và 0 < t ≤ 365 nên ta có:

Với k = 0 thì t = 80 + 182.0 = 80;

Với k = 1 thì t = 80 + 182.1 = 262.

Vậy thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày thứ 80 và ngày thứ 262 trong năm.

b) Để thành phố A có đúng 9 giờ có ánh sáng mặt trời thì:

3sin$\left(\frac{\pi }{182}\left(t-80\right)\right)$+12 = 9

$\iff$ sin$\left(\frac{\pi }{182}\left(t-80\right)\right)$ = -1

$\iff$ $\frac{\pi }{182}$(t-80) = -$\frac{\pi }{2}$ + k2$\pi$ (k$\in$Z)

$\iff$ t - 80 = -91+364k (k$\in$Z)

$\iff$ t = -11+364k (k$\in$Z)

Do t ∈ ℤ và 0 < t ≤ 365 nên ta có:

Với k = 1 thì t = ‒11 + 364.1 = 353.

Vậy thành phố A có đúng 9 giờ có ánh sáng mặt trời vào ngày thứ 353 trong năm.

c) Để thành phố A có đúng 15 giờ có ánh sáng mặt trời thì:

3sin$\left(\frac{\pi }{182}\left(t-80\right)\right)$+12 = 15

$\iff$ sin$\left(\frac{\pi }{182}\left(t-80\right)\right)$ = 1

$\iff$ $\frac{\pi }{182}$(t-80) = $\frac{\pi }{2}$ + k2$\pi$ (k$\in$Z)

$\iff$ t - 80 = 91+364k (k$\in$Z)

$\iff$ t = 171+364k (k$\in$Z)

Do t ∈ ℤ và 0 < t ≤ 365 nên ta có:

Với k = 0 thì t = 171 + 364.0 = 171.

Vậy thành phố A có đúng 15 giờ có ánh sáng mặt trời vào ngày thứ 171 trong năm.

Bài 5 trang 40 Toán 11 Tập 1: Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi người chơi đu nhún đều, cây đu sẽ đưa người chơi đu dao động quanh vị trí cân bằng (Hình 38). Nghiên cứu trò chơi này, người ta thấy khoảng cách h(m) từ vị trí người chơi đu đến vị trí cân bằng được biểu diễn qua thời gian t (s) (với t ≥ 0) bởi hệ thức h = |d| với d = 3cos$\left(\frac{\pi }{3}\left(2t-1\right)\right)$, trong đó ta quy ước d > 0 khi vị trí cân bằng ở phía sau lưng người chơi đu và d < 0 trong trường hợp ngược lại (Nguồn: Đại số và Giải tích 11 Nâng cao, NXBGD Việt Nam, 2020). Vào thời gian t nào thì khoảng cách h là 3 m, 0 m?

Lời giải:

• Để khoảng cách h(m) từ vị trí người chơi đu đến vị trí cân bằng là 3 m thì:

Do t ≥ 0, k ∈ ℤ nên k ∈ {0; 1; 2; …}

Khi đó 

Vậy $t\in \left(\frac{1}{2};2;\frac{7}{2};5;\frac{13}{2};8;\mathrm{...}\right)$ (giây) thì khoảng cách h là 3 m.

• Để khoảng cách h(m) từ vị trí người chơi đu đến vị trí cân bằng là 0 m thì:

Do t ≥ 0, k ∈ ℤ nên k ∈ {0; 1; 2; …}, khi đó $t\in${$\frac{5}{4};\frac{11}{4};\frac{17}{4};\mathrm{...}$}.

Vậy $t\in${$\frac{5}{4};\frac{11}{4};\frac{17}{4};\mathrm{...}$} (giây) thì khoảng cách h là 0 m.

Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác:

Bài 3: Hàm số lượng giác và đồ thị

Bài 4: Phương trình lượng giác cơ bản

Bài tập cuối chương 1

Bài 1: Dãy số

Bài 2: Cấp số cộng

Lý thuyết Phương trình lượng giác cơ bản

1. Khái niệm phương trình tương đương

- Hai phương trình (cùng ẩn) được gọi là tương đương khi chúng có cùng tập nghiệm.

- Nếu phương trình f(x) =0 tương đương với phương trình g(x) =0 thì ta viết $f(x)=0\iff g(x)=0$

*Chú ý: Hai phương trình vô nghiệm là hai phương trình tương đương.

- Các phép biến đổi tương đương:

+ Cộng hay trừ hai vế với cùng một số hoặc cùng một biểu thức.

+ Nhân hoặc chia 2 vế với cùng một số khác 0 hoặc với cùng một biểu thức luôn có giá trị khác 0.

2. Phương trình $\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{x}=m$

Phương trình sinx=m có nghiệm khi và chỉ khi $\left|m\right|\le 1$.

Khi $\left|m\right|\le 1$sẽ tồn tại duy nhất $\alpha \in \left[-\frac{\pi }{2};\frac{\pi }{2}\right]$ thoả mãn $\sin \alpha =m$. Khi đó:

$\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{x}=m\iff \sin x=\sin \alpha$ $\iff [\begin{array}{l}x=\alpha +k2\pi \\ x=\pi -\alpha +k2\pi \end{array}\left(k\in \mathbb{Z}\right)$

* Chú ý:

a, Nếu số đo của góc $\alpha$được cho bằng đơn vị độ thì $\sin x=\sin {\alpha }^o\iff [\begin{array}{l}x={\alpha }^o+k{360}^o\\ x={180}^o-{\alpha }^o+k{360}^o\end{array}\left(k\in \mathbb{Z}\right)$

b, Một số trường hợp đặc biệt

$\begin{array}{l}\sin x=0\iff x=k\pi ,k\in \mathbb{Z}.\\ \sin x=1\iff x=\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z}.\\ \sin x=-1\iff x=-\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z}.\end{array}$

3. Phương trình $\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{x}=m$

Phương trình $\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{x}=m$ có nghiệm khi và chỉ khi $\left|m\right|\le 1$.

Khi $\left|m\right|\le 1$ sẽ tồn tại duy nhất $\alpha \in \left[0;\pi \right]$ thoả mãn $\mathrm{c}\mathrm{o}\mathrm{s}\alpha =m$. Khi đó:

$\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{x}=m\iff \mathrm{c}\mathrm{o}\mathrm{s}\mathrm{x}=\mathrm{c}\mathrm{o}\mathrm{s}\alpha$ $\iff [\begin{array}{l}x=\alpha +k2\pi \\ x=-\alpha +k2\pi \end{array}\left(k\in \mathbb{Z}\right)$

* Chú ý:

a, Nếu số đo của góc $\alpha$được cho bằng đơn vị độ thì $\cos x=\cos {\alpha }^o\iff [\begin{array}{l}x={\alpha }^o+k{360}^o\\ x=-{\alpha }^o+k{360}^o\end{array}\left(k\in \mathbb{Z}\right)$

b, Một số trường hợp đặc biệt

$\begin{array}{l}\mathrm{c}\mathrm{o}\mathrm{s}x=0\iff x=\frac{\pi }{2}+k\pi ,k\in \mathbb{Z}.\\ \mathrm{c}\mathrm{o}\mathrm{s}x=1\iff x=k2\pi ,k\in \mathbb{Z}.\\ \mathrm{c}\mathrm{o}\mathrm{s}x=-1\iff x=\pi +k2\pi ,k\in \mathbb{Z}.\end{array}$

4. Phương trình $\tan x=m$

Phương trình $\tan x=m$có nghiệm với mọi m.

Với mọi $m\in \mathbb{R}$, tồn tại duy nhất $\alpha \in \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ thoả mãn $\tan \alpha =m$. Khi đó:

$\tan \mathrm{x}=m\iff \tan x=\tan \alpha \iff x=\alpha +k\pi ,k\in \mathbb{Z}.$

*Chú ý: Nếu số đo của góc $\alpha$được cho bằng đơn vị độ thì

$\tan x=\tan {\alpha }^o\iff x={\alpha }^o+k{180}^o,k\in \mathbb{Z}.$

5. Phương trình $\cot x=m$

Phương trình $\cot x=m$có nghiệm với mọi m.

Với mọi $m\in \mathbb{R}$, tồn tại duy nhất $\alpha \in \left(0;\pi \right)$ thoả mãn $\cot \alpha =m$. Khi đó:

$\cot \mathrm{x}=m\iff \cot x=\cot \alpha \iff x=\alpha +k\pi ,k\in \mathbb{Z}.$

*Chú ý: Nếu số đo của góc $\alpha$được cho bằng đơn vị độ thì

$\cot x=\cot {\alpha }^o\iff x={\alpha }^o+k{180}^o,k\in \mathbb{Z}.$

6. Sử dụng máy tính cầm tay tìm góc khi biết giá trị lượng giác của nó

Bước 1. Chọn đơn vị đo góc (độ hoặc radian).

Muốn tìm số đo độ, ta ấn: SHIFT $\to$MODE $\to$3 (CASIO FX570VN).

Muốn tìm số đo radian, ta ấn: SHIFT $\to$MODE $\to$4 (CASIO FX570VN).

Bước 2. Tìm số đo góc.

Khi biết SIN, COS, TANG của góc $\alpha$ta cần tìm bằng m, ta lần lượt ấn các phím SHIFT và một trong các phím SIN, COS, TANG rồi nhập giá trị lượng giác m và cuối cùng ấn phím  “BẰNG =”. Lúc này trên màn hình cho kết quả là số đo của góc $\alpha$