Với giải sách bài tập Toán 11 Bài 3: Hàm số lượng giác và đồ thị sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 11. Mời các bạn đón xem:

Giải SBT Toán 11 Bài 3: Hàm số lượng giác và đồ thị

Giải SBT Toán 11 trang 21

Bài 31 trang 21 SBT Toán 11 Tập 1: Tập xác định của hàm số $y=\sqrt{1+\cos 2x}$  là:

A. ∅.

B. ℝ.

C. [– 1; + ∞).

D. 

Lời giải:

Đáp án đúng là: B

Biểu thức $\sqrt{1+\cos 2x}$  có nghĩa khi 1 + cos 2x ≥ 0.

Mà cos 2x ∈ [– 1; 1] nên 1 + cos 2x ≥ 0 với mọi x ∈ ℝ.

Do đó, hàm số $y=\sqrt{1+\cos 2x}$  xác định với mọi x ∈ ℝ.

Bài 32 trang 21 SBT Toán 11 Tập 1: Tập xác định của hàm số $y=\sqrt{\frac{1-\cos x}{1+\sin x}}$  là:

A. ℝ.

B. ∅.

Lời giải:

Đáp án đúng là: C

Biểu thức $\sqrt{\frac{1-\cos x}{1+\sin x}}$  có nghĩa khi 

Do cos x ∈ [– 1; 1] nên 1 – cos x ≥ 0 với mọi x ∈ ℝ.

Và sin x ∈ [– 1; 1] nên 1 + sin x ≥ 0 với mọi x ∈ ℝ.

Do đó để 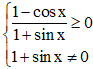  thì 1 + sin x ≠ 0 hay sin x ≠ – 1, khi đó $x\ne -\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z}$ .

Vậy tập xác định của hàm số $y=\sqrt{\frac{1-\cos x}{1+\sin x}}$  là 

Giải SBT Toán 11 trang 22

Bài 33 trang 22 SBT Toán 11 Tập 1: Tập xác định của hàm số $y=\frac{1-\sin x}{\cos x}$  là:

Lời giải:

Đáp án đúng là: C

Biểu thức $\frac{1-\sin x}{\cos x}$  có nghĩa khi cos x ≠ 0 hay $x\ne \frac{\pi }{2}+k\pi ,k\in \mathbb{Z}$ .

Vậy tập xác định của hàm số $y=\frac{1-\sin x}{\cos x}$  là D = 

Bài 34 trang 22 SBT Toán 11 Tập 1: Tập xác định của hàm số $y=\tan x+\frac{1}{1+{\cot }^{2}x}$  là:

Lời giải:

Đáp án đúng là: A

Hàm số $y=\tan x+\frac{1}{1+{\cot }^{2}x}$  xác định khi tan x và cot x xác định (do 1 + cot² x > 0 với mọi x khi cot x xác định).

Mà tan x xác định khi $x\ne \frac{\pi }{2}+k\pi ,k\in \mathbb{Z}$ , cot x xác định khi x ≠ kπ, k ∈ ℤ.

Do đó hàm số $y=\tan x+\frac{1}{1+{\cot }^{2}x}$  xác định khi $x\ne k\frac{\pi }{2},k\in \mathbb{Z}$ .

Vậy tập xác định của hàm số $y=\tan x+\frac{1}{1+{\cot }^{2}x}$  là 

Bài 35 trang 22 SBT Toán 11 Tập 1: Hàm số nào sau đây là hàm số lẻ?

A. y = – 2cos x.

B. y = – 2sin x.

C. y = tan x – cos x.

D. y = – 2 sin x + 2.  

Lời giải:

Đáp án đúng là: B

Xét hàm số y = – 2sin x, ta có:

+ Tập xác định: D = ℝ.

+ Với x ∈ ℝ thì – x ∈ ℝ và f(– x) = – 2sin(– x) = – 2 . (– sin x) = 2 sin x = – f(x).

Do đó, hàm số y = – 2sin x là hàm số lẻ.

Bài 36 trang 22 SBT Toán 11 Tập 1: Hàm số nào sau đây là hàm số chẵn?

A. y = cos x + 5.

B. y = tan x + cot x.

C. y = sin(– x).

D. y = sin x – cos x.

Lời giải:

Đáp án đúng là: A

Xét hàm số y = cos x + 5, ta có:

+ Tập xác định: D = ℝ.

+ Với x ∈ ℝ thì – x ∈ ℝ và f(– x) = cos(– x) + 5 = cos x + 5 = f(x).

Do đó, hàm số y = cos x + 5 là hàm số chẵn.

Bài 37 trang 22 SBT Toán 11 Tập 1: Hàm số y = cos x nghịch biến trên khoảng:

A. (0; π).

B. (π; 2π).

C. $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ .

D. (– π; 0).

Lời giải:

Đáp án đúng là: A

Hàm số y = cos x nghịch biến trên mỗi khoảng (k2π; π + k2π).

Do đó hàm số y = cos x nghịch biến trên khoảng (0; π).

Bài 38 trang 22 SBT Toán 11 Tập 1: Hàm số nào trong các hàm số sau đồng biến trên khoảng $\left(\frac{\pi }{2};\frac{3\pi }{2}\right)$ ?

A. y = sin x.

B. y = cos x.

C. y = tan x.

D. y = cot x.  

Lời giải:

Đáp án đúng là: C

Ta có: $\left(\frac{\pi }{2};\frac{3\pi }{2}\right)=\left(-\frac{\pi }{2}+\pi ;\frac{\pi }{2}+\pi \right)$ .

Do hàm số y = tan x đồng biến trên khoảng $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$  nên hàm số đó cũng đồng biến trên khoảng $\left(\frac{\pi }{2};\frac{3\pi }{2}\right)$ .

Bài 39 trang 22 SBT Toán 11 Tập 1: Hàm số y = sin x đồng biến trên khoảng:

A. $\left(\frac{9\pi }{2};\frac{11\pi }{2}\right)$ .

B. $\left(\frac{11\pi }{2};\frac{13\pi }{2}\right)$ .

C. (10π; 11π).

D. (9π; 10π).

Lời giải:

Đáp án đúng là: B

Ta có: $\left(\frac{11\pi }{2};\frac{13\pi }{2}\right)$ $=\left(-\frac{\pi }{2}+6\pi ;\frac{\pi }{2}+6\pi \right)$ .

Do hàm số y = sin x đồng biến trên khoảng $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$  nên hàm số đó cũng đồng biến trên khoảng $\left(\frac{11\pi }{2};\frac{13\pi }{2}\right)$ .

Bài 40 trang 22 SBT Toán 11 Tập 1: Số giá trị α ∈ [− π; 2π] sao cho $\cos \alpha =\frac{1}{3}$  là:

A. 1.

B. 2.

C. 3.

D. 4.

Lời giải:

Đáp án đúng là: C

Xét đồ thị hàm số y = cos x trên [− π; 2π] và đường thẳng y = $\frac{1}{3}$ .

Ta thấy đường thẳng y = $\frac{1}{3}$  cắt đồ thị hàm số y = cos x trên [− π; 2π] tại 3 điểm.

Khi đó có 3 giá trị của x ∈ [− π; 2π] để $\cos x=\frac{1}{3}$  hay có 3 giá trị của α ∈ [− π; 2π] để $\cos \alpha =\frac{1}{3}$ .

Bài 41 trang 22 SBT Toán 11 Tập 1: Tìm tập xác định của các hàm số:

a) $y=\sqrt{1+\sin 3x}$ ;

b) $y=\frac{\sin 2x}{\sqrt{1-\cos x}}$ ;

c) $y=\frac{\sqrt{1+\cos 2x}}{\sin x}$ .

d) $y=\frac{1}{\sin x+\cos x}$ ;

e) $y=\frac{1}{1+\sin x\cos x}$ ;

g) $y=\sqrt{\cos x-1}$ .

Lời giải:

a) Vì sin 3x ∈ [− 1; 1] nên 1 + sin 3x ≥ 0 với mọi x ∈ ℝ.

Do đó biểu thức $\sqrt{1+\sin 3x}$  có nghĩa với mọi x ∈ ℝ.

Vậy tập xác định của hàm số $y=\sqrt{1+\sin 3x}$  là D = ℝ.

b) Vì cos x ∈ [− 1; 1] nên 1 – cos x ≥ 0 với mọi x ∈ ℝ.

Nên biểu thức $\frac{\sin 2x}{\sqrt{1-\cos x}}$  có nghĩa khi 1 – cos x ≠ 0 hay cos x ≠ 1, tức là x ≠ k2π, k ∈ ℤ.

Vậy tập xác định của hàm số $y=\frac{\sin 2x}{\sqrt{1-\cos x}}$  là 

c) Biểu thức $\frac{\sqrt{1+\cos 2x}}{\sin x}$  có nghĩa khi 

Mà cos 2x ∈ [− 1; 1] nên 1 + cos 2x ≥ 0 với mọi x ∈ ℝ.

Và sin x ≠ 0 khi $x\ne k\pi ,k\in \mathbb{Z}$ .

Vậy tập xác định của hàm số $y=\frac{\sqrt{1+\cos 2x}}{\sin x}$  là 

d) Biểu thức $\frac{1}{\sin x+\cos x}$  có nghĩa khi sin x + cos x ≠ 0

⇔ sin x ≠ – cos x ⇔ tan x ≠ – 1.

Mà tan x ≠ – 1 khi $x\ne -\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}$ .

Vậy tập xác định của hàm số $y=\frac{1}{\sin x+\cos x}$  là 

e) Ta có: 1 + sin x cos x = $1+\frac{\sin 2x}{2}$ .

Vì – 1 ≤ sin 2x ≤ 1 nên $\frac{1}{2}\le 1+\frac{\sin 2x}{2}\le \frac{3}{2}$  với mọi x ∈ ℝ.

Do đó 1 + sin x cos x > 0 với mọi x ∈ ℝ.

Khi đó biểu thức $\frac{1}{1+\sin x\cos x}$  có nghĩa với mọi x ∈ ℝ.

Vậy tập xác định của hàm số $y=\frac{1}{1+\sin x\cos x}$  là D = ℝ.

g) Biểu thức $\sqrt{\cos x-1}$  có nghĩa khi cos x – 1 ≥ 0 hay cos x ≥ 1.

Mà cos x ∈ [− 1; 1] với mọi x ∈ ℝ.

Do đó, biểu thức $\sqrt{\cos x-1}$  có nghĩa khi cos x = 1, tức là x = k2π, k ∈ ℤ.

Vậy tập xác định của hàm số $y=\sqrt{\cos x-1}$  là D = {k2π| k ∈ ℤ}.

Giải SBT Toán 11 trang 23

Bài 42 trang 23 SBT Toán 11 Tập 1: Xét tính chẵn, lẻ của các hàm số:

a) y = sin 2x;

b) y = |sin x|;

c) y = tan² x;

d) $y=\sqrt{1-\cos x}$ ;

e) y = tan x + cot x;

g) y = sin x . cos 3x.

Lời giải:

a) Hàm số y = sin 2x có:

+ Tập xác định: D = ℝ.

+ Với x ∈ ℝ thì – x ∈ ℝ và f(– x) = sin(– 2x) = – sin 2x = – f(x).

Do đó, hàm số y = sin 2x là hàm số lẻ.

b) Hàm số  y = |sin x| có:

+ Tập xác định: D = ℝ.

+ Với x ∈ ℝ thì – x ∈ ℝ và f(– x) = |sin(– x)| = |– sin x| = |sin x| = f(x).

Do đó, hàm số y = |sin x| là hàm số chẵn.

c) Hàm số y = tan² x có:

+ Tập xác định: 

+ Với x ∈ D thì – x ∈ D và f(– x) = tan² (– x) = (– tan x)² = tan² x = f(x).

Do đó, hàm số y = tan² x là hàm số chẵn.

d) Vì cos x ∈ [− 1; 1] nên 1 – cos x ≥ 0 với mọi x ∈ ℝ.

Hàm số $y=\sqrt{1-\cos x}$  có:

+ Tập xác định: D = ℝ.

+ Với x ∈ ℝ thì – x ∈ ℝ và $f\left(-x\right)=\sqrt{1-\cos \left(-x\right)}=\sqrt{1-\cos x}=f\left(x\right)$ .

Do đó, hàm số $y=\sqrt{1-\cos x}$  là hàm số chẵn.

e) Hàm số y = tan x + cot x có:

+ Tập xác định: 

+ Với x ∈ D thì – x ∈ D và f(– x) = tan(– x) + cot(– x) = – tan x – cot x = – (tan x + cot x) = – f(x).

Do đó, hàm số y = tan x + cot x là hàm số lẻ.

g) Hàm số y = sin x . cos 3x có:

+ Tập xác định: D = ℝ.

+ Với x ∈ ℝ thì – x ∈ ℝ và f(– x) = sin(– x) . cos(– 3x) = – sin x . cos 3x = – f(x).

Do đó, hàm số y = sin x . cos 3x là hàm số lẻ.

Bài 43 trang 23 SBT Toán 11 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số:

a) y = 3sin x + 5; 

b) $y=\sqrt{1+\cos 2x}+3$ ;

c) y = 4 – 2sin x cos x;

d) $y=\frac{1}{4-\sin x}$ .  

Lời giải:

a) y = 3sin x + 5

Tập xác định của hàm số là ℝ.

Ta có: ∀x ∈ ℝ, thì – 1 ≤ sin x ≤ 1. Do đó, 2 ≤ 3sin x + 5 ≤ 8.

Vậy giá trị lớn nhất của hàm số bằng 8 khi sin x = 1 hay $x=\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)$ ; giá trị nhỏ nhất của hàm số bằng 2 khi sin x = − 1 hay $x=-\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)$ .

b) $y=\sqrt{1+\cos 2x}+3$

Ta có: ∀x ∈ ℝ, thì – 1 ≤ cos 2x ≤ 1 nên 0 ≤ 1 + cos 2x ≤ 2. (*)

Do đó, tập xác định của hàm số là ℝ.

Từ (*) suy ra $0\le \sqrt{1+\cos 2x}\le \sqrt{2}$  ∀x ∈ ℝ. Do đó $3\le \sqrt{1+\cos 2x}+3\le 3+\sqrt{2}$  ∀x ∈ ℝ.

Vậy giá trị lớn nhất của hàm số đã cho bằng $3+\sqrt{2}$  khi cos 2x = 1 hay x = kπ (k ∈ ℤ); giá trị nhỏ nhất của hàm số bằng 3 khi cos 2x = − 1 hay $x=\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$ .

c) Ta có: y = 4 – 2sin x cos x = 4 – sin 2x.

Tập xác định của hàm số là ℝ.

Ta có: ∀x ∈ ℝ, thì – 1 ≤ sin 2x ≤ 1. Do đó, 3 ≤ 4 – sin 2x ≤ 5.

Vậy giá trị lớn nhất của hàm số bằng 5 khi sin 2x = − 1 hay $x=-\frac{\pi }{4}+k\pi \left(k\in \mathbb{Z}\right)$ ; giá trị nhỏ nhất của hàm số bằng 3 khi sin 2x = 1 hay $x=\frac{\pi }{4}+k\pi \left(k\in \mathbb{Z}\right)$ .

d) $y=\frac{1}{4-\sin x}$

Tập xác định của hàm số là ℝ.

Ta có: ∀x ∈ ℝ, thì – 1 ≤ sin x ≤ 1. Do đó, 3 ≤ 4 – sin x ≤ 5. Suy ra $\frac{1}{3}\ge \frac{1}{4-\sin x}\ge \frac{1}{5}$ .

Khi đó $\frac{1}{5}\le y\le \frac{1}{3}$  ∀x ∈ ℝ.

Vậy giá trị lớn nhất của hàm số bằng $\frac{1}{3}$  khi sin x = 1 hay $x=\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)$ ; giá trị nhỏ nhất của hàm số bằng $\frac{1}{5}$  khi sin x = − 1 hay $x=-\frac{\pi }{2}+k2\pi \left(k\in \mathbb{Z}\right)$ .

Bài 44 trang 23 SBT Toán 11 Tập 1: Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:

a) y = sin x trên khoảng $\left(-\frac{19\pi }{2};-\frac{17\pi }{2}\right),\left(-\frac{13\pi }{2};-\frac{11\pi }{2}\right)$ ;

b) y = cosx trên khoảng (19π; 20π), (– 30π; – 29π).

Lời giải:

a)

+ Ta có: $\left(-\frac{19\pi }{2};-\frac{17\pi }{2}\right)$ $=\left(\frac{\pi }{2}-10\pi ;\frac{3\pi }{2}-10\pi \right)$ .

Do hàm số y = sin x nghịch biến trên khoảng $\left(\frac{\pi }{2};\frac{3\pi }{2}\right)$  nên hàm số đó cũng nghịch biến trên khoảng $\left(-\frac{19\pi }{2};-\frac{17\pi }{2}\right)$ .

+ Ta có: $\left(-\frac{13\pi }{2};-\frac{11\pi }{2}\right)=\left(-\frac{\pi }{2}-6\pi ;\frac{\pi }{2}-6\pi \right)$.

Do hàm số y = sin x đồng biến trên khoảng $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$  nên hàm số đó cũng đồng biến trên khoảng $\left(-\frac{13\pi }{2};-\frac{11\pi }{2}\right)$.

b)

+ Ta có: (19π; 20π) = (– π + 20π; 0 + 20π).

Do hàm số y = cos x đồng biến trên khoảng (– π; 0) nên hàm số đó cũng đồng biến trên khoảng (19π; 20π).

+ Ta có: (– 30π; – 29π) = (0 – 30π; π – 30π).

Do hàm số y = cos x nghịch biến trên khoảng (0; π) nên hàm số đó cũng nghịch biến trên khoảng (– 30π; – 29π).

Bài 45 trang 23 SBT Toán 11 Tập 1: Từ đồ thị hàm số y = cos x, cho biết:

a) Có bao nhiêu giá trị của x trên đoạn [ – 5π; 0] để cos x = 1;

b) Có bao nhiêu giá trị của x trên khoảng $\left(-\frac{9\pi }{2};-\frac{3\pi }{2}\right)$  để cos x = 0.

Lời giải:

Xét đồ thị hàm số y = cos x:

a) Trên đoạn [ – 5π; 0], hàm số y = cos x nhận giá trị bằng 1 với x ∈ {– 4π; – 2π; 0}.

Vậy có 3 giá trị của x trên đoạn [ – 5π; 0] để cos x = 1.

b) Trên khoảng $\left(-\frac{9\pi }{2};-\frac{3\pi }{2}\right)$ , hàm số y = cos x nhận giá trị bằng 0 với 

Vậy có 2 giá trị của x trên khoảng $\left(-\frac{9\pi }{2};-\frac{3\pi }{2}\right)$  để cos x = 0.

Bài 46 trang 23 SBT Toán 11 Tập 1: Từ đồ thị hàm số y = sin x, tìm:

a) Các giá trị của x để sin x = $\frac{1}{2}$ ;

b) Các khoảng giá trị của x để hàm số y = sin x nhận giá trị dương.

Lời giải:

a) Xét đồ thị hàm số y = sin x và đường thẳng y = $\frac{1}{2}$ .

Giá trị của x để sin x = $\frac{1}{2}$  là hoành độ giao điểm của đồ thị hàm số y = sin x và đường thẳng y = $\frac{1}{2}$ .

Dựa vào đồ thị, ta có sin x = $\frac{1}{2}$  khi $x=\frac{\pi }{6}+k2\pi$  và $x=\frac{5\pi }{6}+k2\pi$  với k ∈ ℤ.

b) Xét đồ thị hàm số y = sin x:

Hàm số y = sin x nhận giá trị dương tương ứng với phần đồ thị hàm số đó nằm phía trên trục hoành. Dựa vào đồ thị ở hình vẽ trên, ta suy ra hàm số y = sin x nhận giá trị dương khi x ∈ (k2π; π + k2π) với k ∈ ℤ.

Bài 47 trang 23 SBT Toán 11 Tập 1: Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:

$h\left(t\right)=57\sin \left(\frac{2\pi }{15}t-\frac{\pi }{2}\right)+\mathrm{57,5}$

với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).

a) Tính chu kì của hàm số h(t)?

b) Khi t = 0 (phút) thì khoảng cách từ cabin đến mặt đất bằng bao nhiêu?

c) Khi quay một vòng lần thứ nhất tính từ thời điểm t = 0 (phút), tại thời điểm nào của t thì cabin ở vị trí cao nhất? Ở vị trí đạt được chiều cao là 86 m?

Lời giải:

a) Vì vòng quay trò chơi quay mỗi vòng hết 15 phút nên chu kì của hàm số h(t) bằng 15 phút.

b) Khi t = 0 thì $h\left(0\right)=57\sin \left(\frac{2\pi }{15}.0-\frac{\pi }{2}\right)+\mathrm{57,5}=57\sin \left(-\frac{\pi }{2}\right)+\mathrm{57,5}=\mathrm{0,5}$  (m).

Vậy khi đó khoảng cách từ cabin đến mặt đất bằng 0,5 m.

c)

+ Khi quay một vòng, cabin ở vị trí cao nhất khi h(t) đạt giá trị lớn nhất.

Ta có $h\left(t\right)=57\sin \left(\frac{2\pi }{15}t-\frac{\pi }{2}\right)+\mathrm{57,5}$

Với mọi t ≥ 0 thì $-1\le \sin \left(\frac{2\pi }{15}t-\frac{\pi }{2}\right)\le 1$ , do đó h(t) đạt giá trị lớn nhất khi $\sin \left(\frac{2\pi }{15}t-\frac{\pi }{2}\right)=1$  hay t = 7,5 (phút).

Vậy khi quay một vòng lần thứ nhất tính từ thời điểm t = 0 (phút), tại thời điểm t = 7,5 phút thì cabin ở vị trí cao nhất.

+ Ta có cabin đạt được chiều cao là 86 m khi h(t) = 86 hay $57\sin \left(\frac{2\pi }{15}t-\frac{\pi }{2}\right)+\mathrm{57,5}=86$ , tức là $\sin \left(\frac{2\pi }{15}t-\frac{\pi }{2}\right)=\frac{1}{2}$  hay t = 5 (phút).

Vậy cabin đạt được chiều cao là 86 m lần đầu tiên khi t = 5 (phút).

Xem thêm các bài giải SBT Toán 11 Cánh diều hay, chi tiết khác:

Bài 2: Các phép biến đổi lượng giác

Bài 3: Hàm số lượng giác và đồ thị

Bài 4: Phương trình lượng giác cơ bản

Bài tập cuối chương 1

Bài 1: Dãy số

Bài 2: Cấp số cộng

Lý thuyết Hàm số lượng giác và đồ thị