Với giải Luyện tập 1 trang 32 Toán 11 Tập 1 Cánh diều chi tiết trong Bài 4: Phương trình lượng giác cơ bản giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải bài tập Toán lớp 11 Bài 4: Phương trình lượng giác cơ bản
Luyện tập 1 trang 32 Toán 11 Tập 1: Hai phương trình x – 1 = 0 và =0 có tương đương không? Vì sao?
Lời giải:
Tập nghiệm của phương trình x – 1 = 0 là S1 = {1}.
Tập nghiệm của phương trình là S2 = {1}.
Vì S1 = S2 nên hai phương trình x – 1 = 0 và =0 tương đương.
Lý thuyết Phương trình tương đương
– Định nghĩa:
Hai phương trình (cùng ẩn) được gọi là tương đương nếu chúng có cùng tập nghiệm.
Nếu phương trình f1(x) = g1(x) tương đương với phương trình f2(x) = g2(x) thì ta viết f1(x) = g1(x) ⇔ f2(x) = g2(x).
Chú ý: Khi giải phương tình cần lưu ý tới điều kiện xác định của phương trình (hay gọi tắt là điều kiện của phương trình).
– Định lí sau đây nêu lên một số phép biến đổi tương đương thường sử dụng:
Nếu thực hiện các phép biến đổi sau đây trên một phương trình mà không làm thay đổi điều kiện của nó thì ta được một phương trình mới tương đương.
a) Cộng hay trừ hai vế với cùng một số hoặc cùng một biểu thức.
b) Nhân hoặc chia hai vế với cùng một số khác 0 hoặc với cùng một biểu thức luôn có giá trị khác 0.
Ví dụ 1. Giải phương trình (2x – 1)2 = 3x2 – 7x + 11.
Hướng dẫn giải
Ta có (2x – 1)2 = 3x2 – 7x + 11.
⇔ 4x2 – 4x + 1 = 3x2 – 7x + 11.
⇔ x2 + 3x – 10 = 0.
.
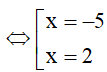
Vậy tập nghiệm của phương trình đã cho là S = {–5; 2}.
Xem thêm các lời giải bài tập Toán lớp 11 Cánh diều hay, chi tiết khác:
Hoạt động 1 trang 32 Toán 11 Tập 1: Cho hai phương trình (với cùng ẩn x):...
Hoạt động 2 trang 33 Toán 11 Tập 1: Khẳng định 3x ‒ 6 = 0 3x = 6 đúng hay sai?...
Luyện tập 2 trang 33 Toán 11 Tập 1: Giải phương trình: (x – 1)2 = 5x – 11...
Luyện tập 3 trang 34 Toán 11 Tập 1: a) Giải phương trình: sin x = ;...
Luyện tập 4 trang 35 Toán 11 Tập 1: Giải phương trình sin2x = sin....
Luyện tập 5 trang 36 Toán 11 Tập 1: a) Giải phương trình: cosx = -...
Luyện tập 6 trang 37 Toán 11 Tập 1: Giải phương trình được nêu trong bài toán mở đầu...
Luyện tập 7 trang 37 Toán 11 Tập 1: a) Giải phương trình: tanx = 1...
Luyện tập 8 trang 39 Toán 11 Tập 1: a) Giải phương trình: cotx = 1...
Bài 1 trang 40 Toán 11 Tập 1: Giải phương trình:...
Bài 2 trang 40 Toán 11 Tập 1: Giải phương trình:...
Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 3: Hàm số lượng giác và đồ thị
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
