Với giải Bài 6 trang 118 Toán lớp 7 Cánh diều chi tiết trong Bài 13: Tính chất ba đường cao của tam giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Bài 13: Tính chất ba đường cao của tam giác

Bài 6 trang 118 Toán 7 Tập 2: Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Chứng minh rằng:

a) Nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau;

b) Nếu tam giác ABC có hai điểm H, I trùng nhau thì tam giác ABC là tam giác đều.

Lời giải:

a)

Chứng minh (Hình vẽ dưới đây):

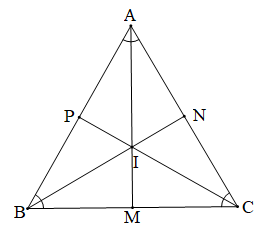
Kéo dài AI cắt BC tại M, kéo dài BI cắt AC tại N, kéo dài CP cắt AB tại P.

Khi đó AM là đường phân giác của $\widehat{BAC}$ nên $\widehat{BAM}=\widehat{CAM};$

Do tam giác ABC đều nên AB = BC = CA.

Xét $∆$ABM và $∆$ACM có:

AB = AC (chứng minh trên),

$\widehat{BAM}=\widehat{CAM}$ (chứng minh trên),

AM là cạnh chung

Do đó $∆$ABM = $∆$ACM  (c.g.c).

Suy ra:

• $\widehat{AMB}=\widehat{AMC}$ (hai góc tương ứng);

• BM = CM (hai cạnh tương ứng).

Vì BM = CM nên M là trung điểm của BC.

Ta có $\widehat{AMB}=\widehat{AMC}$, mà $\widehat{AMB}+\widehat{AMC}=180°$ nên $\widehat{AMB}=\widehat{AMC}=\frac{180°}{2}=90°$.

Khi đó AM $\perp$ BC tại trung điểm M của BC nên AM là đường trung trực của đoạn thẳng BC cũng đồng thời là đường cao và đường trung tuyến kẻ từ A của $∆$ABC.

Chứng minh tương tự ta cũng có:

+) BN là đường trung trực của đoạn thẳng AC, đồng thời là đường cao và đường trung tuyến kẻ từ B của $∆$ABC.

+) CP là đường trung trực của đoạn thẳng AB, đồng thời là đường cao và đường trung tuyến kẻ từ C của $∆$ABC.

Mà AM, BN, CP cắt nhau tại I nên G, H, I, O trùng nhau.

b)

Chứng minh (Hình vẽ dưới đây):

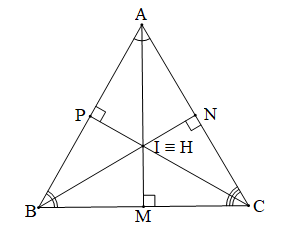
Vì I là giao điểm ba đường phân giác, H là trực tâm của tam giác ABC (giả thiết) nên:

+ AI là đường phân giác và AH là đường cao kẻ từ A của $∆$ABC.

Mà I ≡ H (giả thiết) nên đường phân giác AI trùng với đường cao AH.

+ Tương tự đường phân giác BI trùng đường cao BH;

+ Đường phân giác CI trùng đường cao CH.

Gọi M, N, P lần lượt là chân đường cao (hay cũng chính là đường phân giác) kẻ từ A, B, C đến BC, CA, AB.

Xét $∆$ABM (vuông tại M) và $∆$ACM (vuông tại M) có:

$\widehat{BAM}=\widehat{CAM}$ (do AM là tia phân giác của $\widehat{BAC}$),

AM là cạnh chung

Do đó $∆$ABM = $∆$ACM (cạnh góc vuông – góc nhọn kề).

Suy ra AB = AC (hai cạnh tương ứng). (1)

Xét $∆$ABN (vuông tại N) và $∆$CBN (vuông tại N) có:

BN là cạnh chung,

$\widehat{ABN}=\widehat{CBN}$ (do BN là tia phân giác của $\widehat{ABC}$),

Do đó $∆$ABN = $∆$CBN (cạnh góc vuông – góc nhọn kề).

Suy ra AB = BC (hai cạnh tương ứng). (2)

Từ (1) và (2) suy ra AB = BC = CA do đó tam giác ABC là tam giác đều.

Vậy tam giác ABC đều.