Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Bài 10: Tính chất ba đường trung tuyến của tam giác chi tiết sách Toán 7 Tập 2 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Bài 10: Tính chất ba đường trung tuyến của tam giác

A. Câu hỏi trong bài

Giải Toán 7 trang 104 Tập 2

Câu hỏi khởi động trang 104 Toán 7 Tập 2: Hình 96 minh họa một miếng bìa phẳng có dạng hình tam giác đặt thăng bằng trên đầu ngón tay tại điểm G.

Điểm G được xác định như thế nào?

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Điểm G là trọng tâm của tam giác (hay G là giao điểm của ba đường trung tuyến của tam giác).

Hoạt động 1 trang 104 Toán 7 Tập 2: Quan sát Hình 97 và cho biết các đầu mút của đoạn thẳng AM có đặc điểm gì.

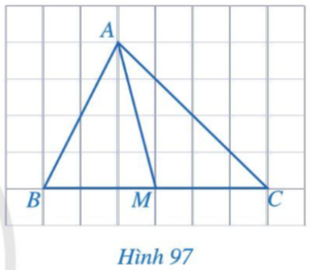
Lời giải:

Ta coi độ dài cạnh của ô vuông nhỏ là 1.

Khi đó độ dài của đoạn thẳng MB bằng 3 lần độ dài cạnh ô vuông nên MB = 3.

Tương tự ta có MC = 3.

Lại thấy M nằm giữa B và C nên M là trung điểm của BC.

Vậy điểm A là một đỉnh của tam giác ABC, điểm M là trung điểm của cạnh BC.

Giải Toán 7 trang 105 Tập 2

Luyện tập 1 trang 105 Toán 7 Tập 2: Trong Hình 101, đoạn thẳng HK là đường trung tuyến của những tam giác nào?

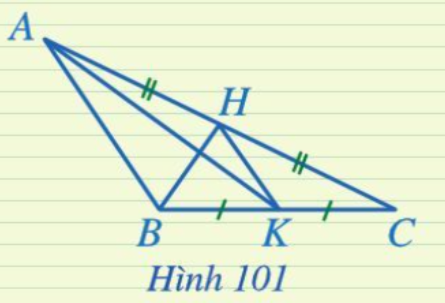
Lời giải:

Quan sát Hình 101 ta thấy:

+ Đoạn thẳng HK là đường trung tuyến của tam giác BHC vì H là đỉnh của tam giác BHC, K là trung điểm của cạnh BC;

+ Đoạn thẳng KH là đường trung tuyến của tam giác AKC vì K là đỉnh của tam giác AKC, H là trung điểm của cạnh AC.

Hoạt động 2 trang 105 Toán 7 Tập 2: Quan sát các đường trung tuyến AM, BN, CP của tam giác ABC trong Hình 102, cho biết ba đường trung tuyến đó có cùng đi qua một điểm hay không.

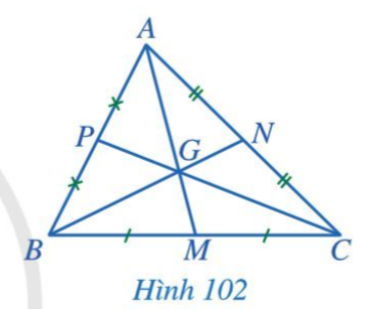
Lời giải:

Quan sát Hình 102, ta thấy ba đường trung tuyến AM, BN, CP của tam giác ABC cùng đi qua điểm G.

Luyện tập 2 trang 105 Toán 7 Tập 2: Cho tam giác PQR có hai đường trung tuyến QM và RK cắt nhau tại G. Gọi I là trung điểm của cạnh QR. Chứng minh rằng ba điểm P, G, I thẳng hàng.

Lời giải:

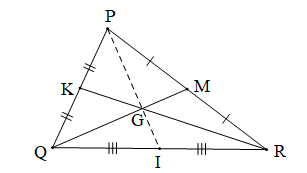
Tam giác PQR có hai đường trung tuyến QM và RK cắt nhau tại G (giả thiết) nên G là trọng tâm của tam giác PQR.

I là trung điểm của cạnh QR nên PI là đường trung tuyến của tam giác PQR kẻ từ đỉnh P.

Mà các đường trung tuyến của tam giác cùng đi qua trọng tâm của tam giác nên trung tuyến PI sẽ đi qua điểm G.

Vậy ba điểm P, G, I thẳng hàng.

Giải Toán 7 trang 106 Tập 2

Hoạt động 3 trang 106 Toán 7 Tập 2: Quan sát các đường trung tuyến AM, BN, CP của tam giác ABC trong Hình 104.

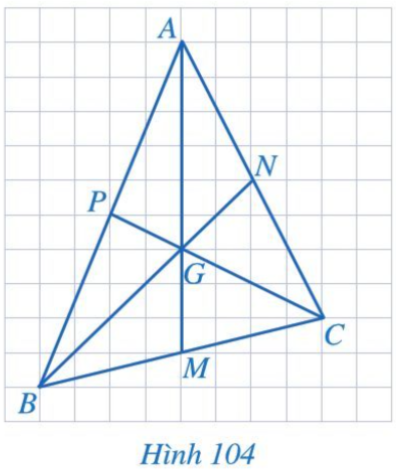
Bằng cách đếm số ô vuông, tìm các tỉ số $\frac{AG}{AM},\frac{BG}{BN},\frac{CG}{CP}.$

Lời giải:

Đếm số ô vuông trong Hình 104, ta thấy:

+) Đoạn thẳng AG đi qua 6 ô vuông, đoạn thẳng AM đi qua 9 ô vuông.

Do đó $\frac{AG}{AM}=\frac{6}{9}=\frac{2}{3}$;  

+) Đoạn thẳng BG đi qua 4 ô vuông, đoạn thẳng BN đi qua 6 ô vuông.

Do đó: $\frac{BG}{BN}=\frac{4}{6}=\frac{2}{3}$;  

+) Đoạn thẳng CG đi qua 4 ô vuông, đoạn thẳng CP đi qua 6 ô vuông.

Do đó: $\frac{CG}{CP}=\frac{4}{6}=\frac{2}{3}$.

B. Bài tập

Giải Toán 7 trang 107 Tập 2

Bài 1 trang 107 Toán 7 Tập 2: Cho tam giác ABC. Ba đường trung tuyến AM, BN, CP đồng quy tại G. Chứng minh:

GA + GB + GC = $\frac{2}{3}$(AM + BN + CP).

Lời giải:

Chứng minh (Hình vẽ dưới đây):

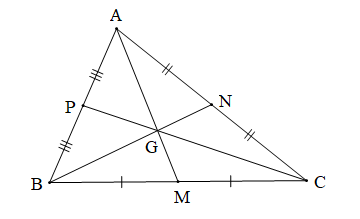
Tam giác ABC có ba đường trung tuyến AM, BN, CP đồng quy tại G nên G là trọng tâm của tam giác ABC.

Khi đó AG = $\frac{2}{3}$AM; BG = $\frac{2}{3}$BN; CG = $\frac{2}{3}$CP (tính chất trọng tâm của tam giác)

Do đó GA + GB + GC = $\frac{2}{3}$AM + $\frac{2}{3}$BN + $\frac{2}{3}$CP = $\frac{2}{3}$(AM + BN + CP).

Vậy GA + GB + GC = $\frac{2}{3}$(AM + BN + CP).

Bài 2 trang 107 Toán 7 Tập 2: Cho tam giác ABC cân tại A, hai đường trung tuyến BM và CN cắt nhau tại G. Chứng minh:

a) BM = CN;

b) $∆$GBC cân tại G.

Lời giải:

Chứng minh (Hình vẽ dưới đây):

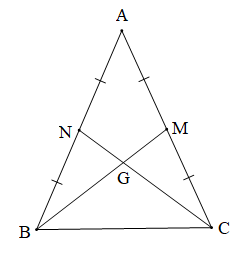
a) Tam giác ABC cân tại A (giả thiết) nên AB = AC (1).

Do BM đường trung tuyến của tam giác ABC nên M là trung điểm của AC do đó $AM=MC=\frac{1}{2}AC$  (2)

CN là đường trung tuyến của tam giác ABC nên N là trung điểm của AB do đó $AN=NB=\frac{1}{2}AB$  (3)

Từ (1), (2) và (3) ta có: AM = AN.

Xét $∆$ABM và $∆$ACN có:

AM = AN (chứng minh trên).

$\widehat{A}$ là góc chung,

AB = AC (chứng minh trên)

Do đó $∆$ABM = $∆$ACN (c.g.c)

Suy ra BM = CN (2 cạnh tương ứng).

Vậy BM = CN.

b) Tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G nên G là trọng tâm của tam giác ABC.

Suy ra BG = $\frac{2}{3}$BM; CG = $\frac{2}{3}$CN (tính chất trọng tâm của tam giác).

Mà BM = CN (chứng minh câu a)

Do đó BG = CG.

Tam giác GBC có BG = CG nên tam giác GBC cân tại G.

Vậy $∆$GBC cân tại G.

Bài 3 trang 107 Toán 7 Tập 2: Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Trên tia đối của tia MA lấy điểm D sao cho MD = MG. Chứng minh:

a) GA = GD;

b) $∆$MBG = $∆$MCD;

c) CD = 2GN.

Lời giải:

Chứng minh (Hình vẽ dưới đây):

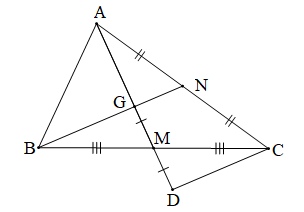
a) Tam giác ABC có hai đường trung tuyến AM, BN cắt nhau tại G (giả thiết) nên G là trọng tâm của tam giác ABC.

Khi đó GM = $\frac{1}{2}$GA (tính chất trọng tâm của tam giác).

Điểm D nằm trên tia đối của tia MA và MD = MG (giả thiết) nên M là trung điểm của GD.

Suy ra GM = $\frac{1}{2}$GD.

Do đó GA = GD.

Vậy GA = GD.

b) Do M là trung điểm của GD nên MG = MD.

Xét $∆$MBG và $∆$MDC có:

MB = MC (giả thiết),

$\widehat{GMB}=\widehat{DMC}$ (hai góc đối đỉnh),

MG = MD (chứng minh trên),

Do đó $∆$MBG = $∆$MDC (c.g.c).

c) Vì $∆$MBG = $∆$MDC (chứng minh câu b) nên CD = BG (hai cạnh tương ứng).

Lại có G là trọng tâm của tam giác ABC nên BG = 2GN.

Do đó CD = 2GN.

Vậy CD = 2GN.

Bài 4 trang 107 Toán 7 Tập 2: Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Gọi H là hình chiếu của A lên đường thẳng BC. Giả sử H là trung điểm của đoạn thẳng BM. Chứng minh:

a) $∆$AHB = $∆$AHM;

b) $AG=\frac{2}{3}AB$.

Lời giải:

Chứng minh (Hình vẽ dưới đây):

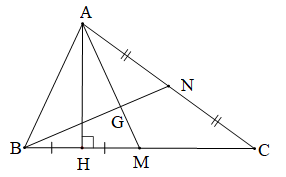
a) Vì H là hình chiếu của A trên BC nên AH $\perp$ BC

Do đó $∆$AHB vuông tại H và $∆$AHM vuông tại H.

Xét $∆$AHB (vuông tại H) và $∆$AHM (vuông tại H) có:

AH là cạnh chung,

HB = HM (H là trung điểm của BM).

Do đó $∆$AHB = $∆$AHM (hai cạnh góc vuông).

Vậy $∆$AHB = $∆$AHM.

b) Vì $∆$AHB = $∆$AHM (chứng minh câu a)

Nên AB = AM (hai cạnh tương ứng).

$∆$ABC có hai đường trung tuyến AM, BN cắt nhau tại G nên G là trọng tâm của $∆$ABC.

Suy ra AG = $\frac{2}{3}$AM (tính chất trọng tâm của tam giác)

Do đó AG = $\frac{2}{3}$AB.

Vậy $AG=\frac{2}{2}AB.$ 

Bài 5 trang 107 Toán 7 Tập 2: Hình 107 là mặt cắt đứng của một ngôi nhà có mái dốc. Mỗi tầng cao 3,3 m. Mặt cắt mái nhà có dạng tam giác ABC cân tại A với đường trung tuyến AH dài 1,2 m. Tại vị trí O là trọng tâm tam giác ABC, người ta làm tâm cho một cửa sổ có dạng hình tròn.

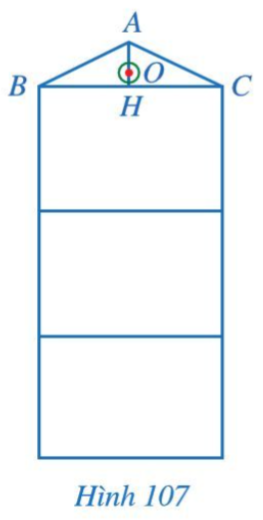
a) AH có vuông góc với BC không? Vì sao?

b) Vị trí O ở độ cao bao nhiêu mét so với mặt đất?

Lời giải:

a) DABC cân tại A nên AB = AC và $\widehat{ABH}=\widehat{ACH}$.

Lại có AH là đường trung tuyến của $∆$ABC nên H là trung điểm của BC.

Do đó BH = CH.

Xét $∆$ABH và $∆$ACH có:

AB = AC (chứng minh trên),

$\widehat{ABH}=\widehat{ACH}$ (chứng minh trên),

BH = CH (chứng minh trên),

Do đó $∆$ABH = $∆$ACH (c.g.c).

Suy ra $\widehat{AHB}=\widehat{AHC}$ (hai góc tương ứng).

Mà $\widehat{AHB}+\widehat{AHC}=180°$ 

Nên $\widehat{AHB}=\widehat{AHC}=\frac{180°}{2}=90°$ 

Hay AH $\perp$ BC.

Vậy AH $\perp$ BC.

b) Vì O là trọng tâm của tam giác ABC nên OH = $\frac{1}{3}$AH (tính chất trong tâm tam giác)

Mà AH = 1,2 m

Do đó OH = $\frac{1}{3}$. 1,2 = 0,4 m.

Vì mỗi tầng cao 3,3 m mà ngôi nhà ba tầng nên vị trí O ở độ cao so với mặt đất là:

0,4 + 3,3 . 3 = 10,3 (m)

Vậy vị trí O ở độ cao 10,3 m so với mặt đất.

Xem thêm các bài giải SGK Toán lớp 7 Cánh diều hay, chi tiết:

Giải SGK Toán 7 Bài 9: Đường trung trực của một đoạn thẳng

Giải SGK Toán 7 Bài 10: Tính chất ba đường trung tuyến của tam giác

Giải SGK Toán 7 Bài 11: Tính chất ba đường phân giác của tam giác

Giải SGK Toán 7 Bài 12: Tính chất ba đường trung trực của tam giác

Giải SGK Toán 7 Bài 13: Tính chất ba đường cao của tam giác

Lý thuyết Tính chất ba đường trung tuyến của tam giác

1. Đường trung tuyến của tam giác

– Trong tam giác ABC (hình bên dưới), đoạn thẳng AM nối đỉnh A với trung điểm M của cạnh BC được gọi là đường trung tuyến (xuất phát từ đỉnh A hoặc tương ứng với cạnh BC).

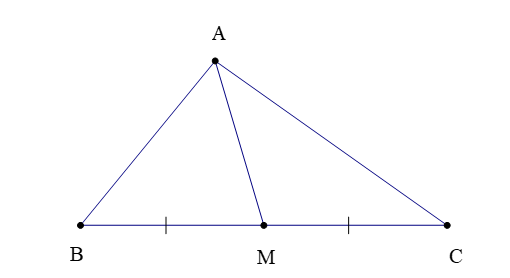
Đôi khi, đường thẳng AM cũng được gọi là đường trung tuyến của ∆ABC.

Ví dụ: Quan sát hình bên dưới và cho biết trong hình có bao nhiêu đường trung tuyến?

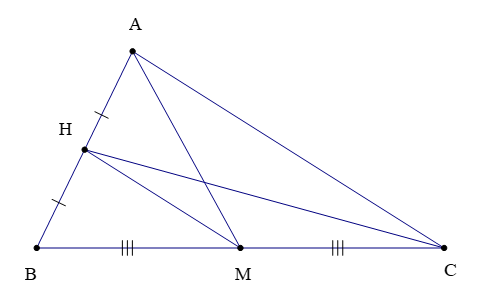
Hướng dẫn giải

Quan sát hình vẽ ta có:

• A là đỉnh của ∆ABC và M là trung điểm của BC nên đoạn thẳng AM là đường trung tuyến của ∆ABC.

• C là đỉnh của ∆ABC và H là trung điểm của AB nên đoạn thẳng CH là đường trung tuyến của ∆ABC.

• M là đỉnh của ∆ABM và H là trung điểm của AB do đó MH là đường trung tuyến của ∆ABM.

• H là đỉnh của ∆HBC và M là trung điểm của BC nên đoạn thẳng HM là đường trung tuyến của ∆HBC.

Vậy trong hình vẽ trên có tất cả 4 đường trung tuyến.

– Chú ý: Mỗi tam giác có ba đường trung tuyến.

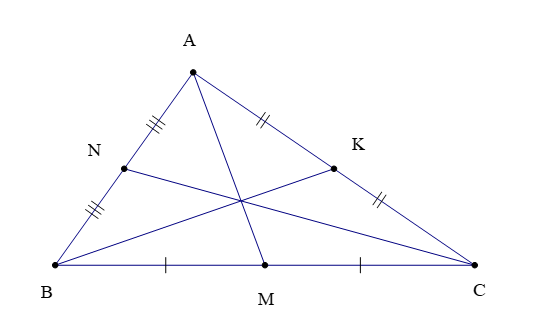
Ví dụ: Tam giác ABC (hình vẽ dưới) có ba đường trung tuyến là AM, BK và CN.

2. Tính chất ba đường trung tuyến của tam giác

– Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm đó được gọi là trọng tâm của tam giác.

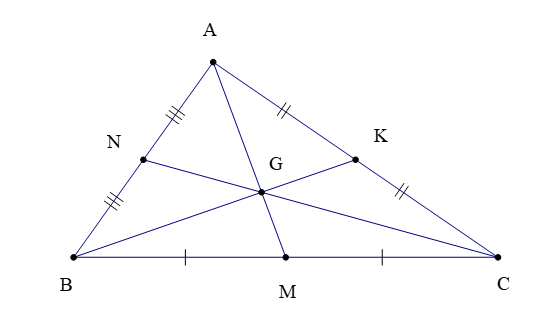
Chú ý: Trong tam giác ABC (hình vẽ dưới) có ba đường trung tuyến AM, BK, CN cùng đi qua điểm G, ta còn nói chúng đồng quy tại điểm G.

Để xác định trọng tâm của một tam giác, ta chỉ cần vẽ hai đường trung tuyến bất kì và xác định giao điểm của hai đường đó.

Nhận xét: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng $\frac{2}{3}$ độ dài đường trung tuyến đi qua đỉnh ấy.

Lưu ý: Trong ∆ABC, với AM là đường trung tuyến và G là trọng tâm ta có:

$\frac{\text{GM}}{\text{AM}}=\frac{1}{3},\frac{\text{GM}}{\text{GA}}=\frac{1}{2}$

Ví dụ: Cho ∆ABC như hình vẽ, biết AM = 18 cm và BN = 21 cm.

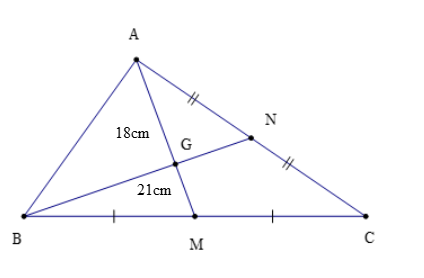
a) Chứng minh: G là trọng tâm của ∆ABC.

b) Tính độ dài AG, GN.

Hướng dẫn giải

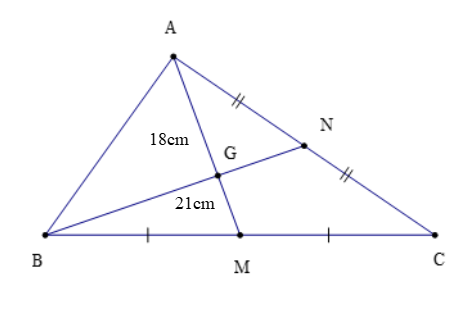
Theo hình vẽ trên ta có:

A là đỉnh của ∆ABC và M là trung điểm của BC nên đoạn thẳng AM là đường trung tuyến của ∆ABC.

B là đỉnh của ∆ABC và N là trung điểm của AC nên đoạn thẳng BN là đường trung tuyến của ∆ABC.

Mà hai đường trung tuyến AM và BN cắt nhau tại G do đó G là trọng tâm của ∆ABC.

Vậy G là trọng tâm của ∆ABC.

b) Theo phần a ta có: G là trọng tâm của ∆ABC nên $\text{AG = }\frac{2}{3}\text{AM}$ (tính chất trọng tâm của tam giác)

Hay $\text{AG = }\frac{2}{3}.18=12\left(\mathrm{cm}\right)$

Vì BN là đường trung tuyến của ∆ABC và G là trọng tâm của ∆ABC

Suy ra $\frac{\text{GN}}{\text{BN}}=\frac{1}{3}$ hay $\text{GN = }\frac{1}{3}\text{BN = }\frac{1}{3}.21=7\left(\text{cm}\right)$

Vậy AG = 12 cm, GN = 7 cm.