Với giải Bài 2 trang 107 Toán lớp 7 Cánh diều chi tiết trong Bài 10: Tính chất ba đường trung tuyến của tam giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Bài 10: Tính chất ba đường trung tuyến của tam giác

Bài 2 trang 107 Toán 7 Tập 2: Cho tam giác ABC cân tại A, hai đường trung tuyến BM và CN cắt nhau tại G. Chứng minh:

a) BM = CN;

b) $∆$GBC cân tại G.

Lời giải:

Chứng minh (Hình vẽ dưới đây):

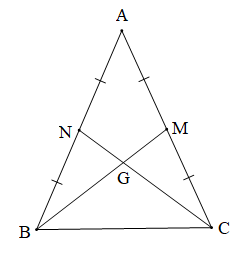
a) Tam giác ABC cân tại A (giả thiết) nên AB = AC (1).

Do BM đường trung tuyến của tam giác ABC nên M là trung điểm của AC do đó $AM=MC=\frac{1}{2}AC$  (2)

CN là đường trung tuyến của tam giác ABC nên N là trung điểm của AB do đó $AN=NB=\frac{1}{2}AB$  (3)

Từ (1), (2) và (3) ta có: AM = AN.

Xét $∆$ABM và $∆$ACN có:

AM = AN (chứng minh trên).

$\widehat{A}$ là góc chung,

AB = AC (chứng minh trên)

Do đó $∆$ABM = $∆$ACN (c.g.c)

Suy ra BM = CN (2 cạnh tương ứng).

Vậy BM = CN.

b) Tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G nên G là trọng tâm của tam giác ABC.

Suy ra BG = $\frac{2}{3}$BM; CG = $\frac{2}{3}$CN (tính chất trọng tâm của tam giác).

Mà BM = CN (chứng minh câu a)

Do đó BG = CG.

Tam giác GBC có BG = CG nên tam giác GBC cân tại G.

Vậy $∆$GBC cân tại G.