Sách bài tập Toán 7 Bài 10 (Cánh diều): Tính chất ba đường trung tuyến của tam giác

Van Anh Ngày: 23-09-2024 Lớp 7

3.1 K

Với giải sách bài tập Toán 7 Bài 10: Tính chất ba đường trung tuyến của tam giác sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 10: Tính chất ba đường trung tuyến của tam giác

Giải SBT Toán 7 trang 89 Tập 2

Bài 70 trang 89 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC cân tại A có hai trung tuyến BM và CN cắt nhau tại G. Chứng minh:

a) BM = CN;

b) Tam giác GBC là tam giác cân;

c) AG vuông góc với BC.

Lời giải:

Cho tam giác ABC cân tại A có hai trung tuyến BM và CN cắt nhau tại G

a) Vì tam giác ABC cân tại A nên AB = AC, $\hat{A B C} = \hat{A C B}$ .

Vì BM, CN là đường trung tuyến của tam giác ABC nên M, N lần lượt là trung điểm của AC và AB.

Do đó AM = MC, AN = NB.

Mà AB = AC

Suy ra AM = MC = AN = NB.

Xét ∆ABM và ∆ACN có:

AB = AC (chứng minh trên),

$\hat{B A C}$ là góc chung,

AM = AN (chứng minh trên)

Do đó ∆ABM = ∆ACN (c.g.c).

Suy ra BM = CN (hai cạnh tương ứng).

Vậy BM = CN.

b) Do ∆AMB = ∆ANC (câu a) suy ra $\hat{A B M} = \hat{A C N}$ (hai góc tương ứng).

Ta có $\hat{A B C} = \hat{A B M} + \hat{M B C}$ , $\hat{A C B} = \hat{A C N} + \hat{N C B}$ .

Mà $\hat{A B C} = \hat{A C B}$ và $\hat{A B M} = \hat{A C N}$ .

Nên $\hat{M B C} = \hat{N C B}$ hay $\hat{G B C} = \hat{G C B}$

Suy ra tam giác GBC cân tại G.

Vậy tam giác GBC cân tại G

c) Ta có AB = AC nên A nằm trên đường trung trực của đoạn thẳng BC.

Theo câu b tam giác GBC cân tại G nên GB = GC (hai cạnh bên).

Do đó G nằm trên trung trực của đoạn thẳng BC.

Suy ra AG là đường trung trực của đoạn thẳng BC nên AG vuông góc với BC tại trung điểm của BC.

Vậy AG vuông góc với BC.

Bài 71 trang 89 sách bài tập Toán lớp 7 Tập 2:Cho tam giác ABC có trọng tâm G. Gọi M là trung điểm của BC. Trên tia đối của MG lấy điểm D sao cho MD = MG.

a) Chứng minh CG là trung tuyến của tam giác ACD.

b) Chứng minh BG song song với CD.

c) Gọi I là trung điểm của BD; AI cắt BG tại F. Chứng minh AF = 2FI.

Lời giải:

Cho tam giác ABC có trọng tâm G. Gọi M là trung điểm của BC. Trên tia đối của MG

a) Vì G là trọng tâm tam giác ABC nên GM = $\frac{1}{2}$ GA.

Mà MD = MG (giả thiết) nên M là trung điểm của GD và GM = $\frac{1}{2}$ GD.

Suy ra GD = GA.

Do đó CG là trung tuyến của tam giác ACD.

Vậy CG là trung tuyến của tam giác ACD.

b) Xét ∆BGM và ∆CDM có:

GM = DM (giả thiết),

$\hat{G M B} = \hat{D M C}$ (hai góc đối đỉnh),

MB = MC (vì M là trung điểm của BC)

Nên ∆BGM = ∆CDM (c.g.c).

Suy ra $\hat{B G M} = \hat{C D M}$ (hai góc tương ứng).

Mà chúng ở vị trí so le trong nên BG // CD.

Vậy BG // CD.

c) Trong tam giác ABD có AI và BG là hai đường trung tuyến, AI và BG cắt nhau tại F.

Do đó F là trọng tâm của tam giác ABD.

Suy ra FI = $\frac{1}{2}$ FA hay AF = 2FI.

Vậy AF = 2FI.

Giải SBT Toán 7 trang 90 Tập 2

Bài 72 trang 90 sách bài tập Toán lớp 7 Tập 2: Chứng minh: Nếu một tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân.

Lời giải:

Chứng minh: Nếu một tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân

Tam giác ABC có hai trung tuyến BM và CN bằng nhau.

Gọi G là giao điểm của BM và CN.

Theo tính chất trọng tâm tam giác có: BG = $\frac{2}{3}$ BM và CG = $\frac{2}{3}$ CN.

Vì BM = CN nên BG = CG.

Suy ra tam giác BGC cân tại G.

Do đó $\hat{G B C} = \hat{G C B}$ (hai góc ở đáy).

Xét ∆MBC và ∆NCB có:

BC là cạnh chung,

$\hat{M B C} = \hat{N C B}$ (do $\hat{G B C} = \hat{G C B}$ ),

MB = NC (giả thiết)

Do đó ∆MBC = ∆NCB (c.g.c)

Suy ra $\hat{M C B} = \hat{N B C}$ (hai góc tương ứng).

Khi đó tam giác ABC cân tại A.

Vậy nếu một tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân.

Bài 73 trang 90 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC đều và có G là trọng tâm.

a) Chứng minh GA = GB = GC.

b) Trên tia AG lấy điểm D sao cho GD = GA. Chứng minh tam giác BGD là tam giác đều.

Lời giải:

a) • Do tam giác ABC đều nên AB = BC = AC.

Gọi M, N lần lượt là trung điểm của BC và AB.

Khi đó AN = NB = $\frac{1}{2}$ AB = $\frac{1}{2}$ BC = BM = MC.

Xét ∆ABM và ∆CBN có:

AB = BC (giả thiết),

$\hat{A B C}$ là góc chung,

BM = BN (chứng minh trên)

Do đó ∆ABM = ∆CBN (c.c.c).

Suy ra AM = CN (hai cạnh tương ứng).

• Vì G là trọng tâm tam giác ABC

Nên AG = $\frac{2}{3}$ AM và CG = $\frac{2}{3}$ CN (tính chất trọng tâm của tam giác).

Mà AM = CN.

Suy ra GA = GC.

Chứng minh tương tự ta có GA = GB.

Do đó GA = GB = GC.

Vậy GA = GB = GC.

b) Ta có GA = GB (theo câu a) và GA = GD (giả thiết).

Nên GD = GB (1)

Ta có G là trọng tam giác ABC nên GM = $\frac{1}{2}$ GA.

Mà GA = GD nên GM = $\frac{1}{2}$ GD.

Do đó GM = MD = $\frac{1}{2}$ GD.

Xét ∆GMC và ∆DMB có:

MB = MC (chứng minh câu a),

$\hat{G M C} = \hat{D M B}$ (hai góc đối đỉnh),

MG = MD (chứng minh trên).

Do đó ∆GMC = ∆DMB (c.g.c)

Suy ra GC = DB (hai cạnh tương ứng).

Lại có GC = GB (theo câu a)

Nên GB = DB (2)

Từ (1) và (2) suy ra GD = GB = DB.

Do đó tam giác BGD là tam giác đều.

Vậy tam giác BGD là tam giác đều.

Bài 74 trang 90 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC có đường trung tuyến BD. Trên tia đối của tia DB lấy điểm E sao cho DE = BD. Gọi M, N lần lượt là trung điểm của BC, CE. Gọi I, K lần lượt là giao điểm của AM, AN với BE. Chứng minh BI = IK = KE.

Lời giải:

Xét tam giác ABC có BD và AM là các đường trung tuyến, BD cắt AM tại I.

Suy ra I là trọng tâm của tam giác ABC.

Nên BI = $\frac{2}{3}$ BD (1)

Xét tam giác AEC có ED và AN là các đường trung tuyến, ED cắt AN tại K.

Suy ra K là trọng tâm của tam giác AEC.

Nên EK = $\frac{2}{3}$ ED (2)

Mặt khác BD = DE, DB + DE = BE

Nên BD = DE = $\frac{1}{2}$ BE (3)

Từ (1), (2) và (3) ta có:

BI = EK = $\frac{2}{3}$ BD = $\frac{2}{3} . \frac{1}{2}$ BE = $\frac{1}{3}$ BE.

Ta lại có: BI + IK + KE = BE.

Suy ra $\frac{1}{3}$ BE + IK + $\frac{1}{3}$ BE = BE

Suy ra IK = $\frac{1}{3}$ BE.

Do đó BI = IK = EK (cùng bằng $\frac{1}{3}$ BE).

Vậy BI = IK = EK.

Bài 75 trang 90 sách bài tập Toán lớp 7 Tập 2: Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. Chứng minh rằng $\hat{B A C} = 90 °$ .

Lời giải:

Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. Chứng minh rằng góc BAC = 90 độ

Ta có: AM = $\frac{1}{2}$ BC, BM = MC nên AM = BM = MC.

Suy ra hai tam giác AMB và AMC cân tại M.

Do đó $\hat{B} = {\hat{A}}_{1}, \hat{C} = {\hat{A}}_{2}$

Xét DABC có $\hat{B} + \hat{C} + \hat{B A C} = 180 °$ (tổng ba góc của một tam giác)

Suy ra ${\hat{A}}_{1} + {\hat{A}}_{2} + \hat{B A C} = 180 °$ hay $\hat{B A C} + \hat{B A C} = 180 °$

Nên $2 \hat{B A C} = 180 °$

Do đó $\hat{B A C} = \frac{180 °}{2} = 90 °$

Vậy $\hat{B A C} = 90 °$ .

Bài 76 trang 90 sách bài tập Toán lớp 7 Tập 2: Cho tam giác nhọn ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Trên cạnh AC lấy điểm E sao cho AE = $\frac{1}{3}$ AC.

a) Chứng minh E là trọng tâm tam giác BCD.

b) Gọi M là trung điểm DC. Chứng minh ba điểm B, M, E thẳng hàng.

Lời giải:

Cho tam giác nhọn ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = AB

a) Ta có AE = $\frac{1}{3}$ AC nên CE = $\frac{2}{3}$ AC

Trong tam giác BCD có CA là trung tuyến và CE = $\frac{2}{3}$ AC.

Suy ra E là trọng tâm tam giác BCD.

Vậy E là trọng tâm tam giác BCD.

b) Trong tam giác BCD có CA và BM là hai đường trung tuyến nên BM cắt CA tại trọng tâm của tam giác.

Mà E là trọng tâm của tam giác BCD (theo câu a) nên điểm E thuộc đường thẳng BM.

Hay ba điểm B, E, M thẳng hàng.

Vậy ba điểm B, E, M thẳng hàng.

Bài 77 trang 90 sách bài tập Toán lớp 7 Tập 2: Cho tam giác ABC cân tại A có đường trung tuyến AD, G là trọng tâm. Trên tia đối của tia DA lấy điểm E sao cho DE = DG.

a) Chứng minh BG = GC = CE = BE.

b) Chứng minh ∆ABE = ∆ACE.

c) Nếu CG = $\frac{1}{2}$ AE thì tam giác ABC là tam giác gì? Vì sao?

Lời giải:

Cho tam giác ABC cân tại A có đường trung tuyến AD, G là trọng tâm

a) Xét tam giác ABC cân tại A nên AB = AC (hai cạnh bên).

Xét ∆ABD và ∆ACD có:

AB = AC (do ∆ABC cân tại A),

DB = DC (do D là trung điểm của BC),

AD là cạnh chung

Do đó ∆ABD = ∆ACD (c.c.c)

Suy ra $\hat{A D B} = \hat{A D C}$ (hai góc tương ứng).

Mà $\hat{A D B} + \hat{A D C} = 180 °$ (hai góc kề bù)

Nên $\hat{A D B} = \hat{A D C} = \frac{180 °}{2} = 90 °$

Suy ra AD vuông góc với BC.

Mặt khác D là trung điểm của BC

Do đó AD là đường trưng trực của đoạn thẳng BC.

Suy ra GB = GC (1)

Lại có điểm E nằm trên đường thẳng AD nên E cũng nằm trên đường trung trực của BC.

Do đó EB = EC (2)

Xét ∆BGD và ∆BED có:

$\hat{B D G} = \hat{B D E} (= 90 °)$ ,

BG là cạnh chung,

DG = DE (giả thiết)

Do đó ∆BGD = ∆BED (hai cạnh góc vuông)

Suy ra BG = BE (3)

Từ (1), (2) và (3) suy ra BG = GC = CE = BE.

Vậy BG = GC = CE = BE.

b) Xét ∆ABE và ∆ACE có:

AB = AC (do ∆ABC cân tại A),

BE = CE (chứng minh câu a),

AE là cạnh chung

Do đó ∆ABE = ∆ACE (c.c.c).

Vậy ∆ABE = ∆ACE.

c) Ta có GD = ED (giả thiết) nên GD = $\frac{1}{2}$ GE

Mà G là trọng tâm của tam giác ABC nên GD = $\frac{1}{2}$ AG.

Do đó AG = GE hay G là trung điểm của AE nên GE = $\frac{1}{2}$ AE.

Mặt khác CG = $\frac{1}{2}$ AE

Suy ra GE = GC.

Theo câu a ta lại có GC = EC.

Khi đó GC = GE = EC.

+) Tam giác CGE có GC = GE = EB nên tam giác CGE là tam giác đều

Do đó $\hat{C G E} = 60 °$

Suy ra:

• $\hat{C G D} + \hat{G C D} = 90 °$ (tổng hai góc nhọn trong tam giác vuông CGD bằng 90°)

Suy ra $\hat{G C D} = 90 ° - \hat{C G D} = 90 ° - 60 ° = 30 °$

• $\hat{C G E} + \hat{A G C} = 180 °$ (hai góc kề bù)

Nên $\hat{A G C} = 180^{o} - \hat{C G E} = 180^{o} - 60^{o} = 120^{o}$

Mà GA = GC nên tam giác AGC cân tại G, do đó $\hat{G A C} = \hat{G C A}$

Lại có $\hat{G A C} + \hat{G C A} + \hat{A G C} = 180 °$ (tổng ba góc của tam giác AGC).

Do đó $\hat{G A C} = \hat{G C A} = \frac{180 ° - \hat{A G C}}{2} = \frac{180 ° - 120 °}{2} = 30 °$

+) Ta có $\hat{A C B} = \hat{A C G} + \hat{G C B}$ (hai góc kề nhau)

Hay $\hat{A C B} = 30 ° + 30 ° = 60 °$

Tam giác cân ABC có $\hat{A C B} = 60 °$ nên là tam giác đều.

Vậy tam giác ABC đều.

Bài 78 trang 90 sách bài tập Toán lớp 7 Tập 2: Cho tam giác DEF cân tại D có đường trung tuyến EM. Trên tia đối của tia ME lấy điểm N sao cho MN = ME.

a) Chứng minh DE = FN và tam giác DFN là tam giác cân.

b) Trên tia đối của tia FD lấy điểm A sao cho FA = FD. Chứng minh F là trọng tâm của tam giác NEA.

c) Chứng minh tam giác DNA là tam giác vuông.

d) Kẻ EB vuông góc với NA (B ∈ NA). Chứng minh ba điểm E, F, B thẳng hàng.

Lời giải:

Cho tam giác DEF cân tại D có đường trung tuyến EM. Trên tia đối của tia ME lấy điểm N

a) Xét ∆DME và ∆FMN có:

DM = FM (vì M là trung điểm của DF),

$\hat{D M E} = \hat{F M N}$ (hai góc đối đỉnh),

ME = MN (giả thiết)

Do đó ∆DME = ∆FMN (c.g.c)

Suy ra DE = FN (hai cạnh tương ứng).

Vì tam giác DFE cân tại D nên DE = DF.

Do đó DE = DF = FN.

Tam giác DFN có DF = FN nêntam giác DFN cân tại F.

Vậy tam giác DFN cân tại F.

b) Ta có MD = MF = $\frac{1}{2}$ DF và FA = FD nên MF = $\frac{1}{2}$ FA

Mà AF + FM = AM nên AF + $\frac{1}{2}$ AF = AM

Suy ra $\frac{3}{2}$ AF = AM hay AF = $\frac{2}{3}$ AM.

Trong tam giác NEA có AM là trung tuyến và AF = $\frac{2}{3}$ AM nên F là trọng tâm của tam giác NEA.

Vậy F là trọng tâm của tam giác NEA.

c) • Ta có: DF = FN, DF = FA nên AF = FN.

Suy ra tam giác FNA cân tại F.

Do đó $\hat{F A N} = \hat{F N A}$ (hai góc ở đáy)

•Vì tam giác DFN cân tại F nên $\hat{F D N} = \hat{F N D}$ (hai góc ở đáy)

• Xét ∆DNA có $\hat{A D N} + \hat{D N A} + \hat{N A D} = 180 °$ (tổng ba góc của một tam giác)

Suy ra $\hat{F N D} + \hat{D N A} + \hat{F N A} = 180 °$

Hay $(\hat{F N D} + \hat{F N A}) + \hat{D N A} = \hat{D N A} + \hat{D N A} = 180 °$

Suy ra $2 \hat{D N A} = 180 °$

Do đó $\hat{D N A} = \frac{180 °}{2} = 90 °$

Vậy tam giác DNA là tam giác vuông tại N.

d) Xét ∆DMN và ∆FME có:

DM = FM (vì M là trung điểm của DF),

$\hat{D M N} = \hat{F M E}$ (hai góc đối đỉnh),

EM = MN (giả thiết)

Do đó ∆DMN = ∆FME (c.g.c)

Suy ra $\hat{M D N} = \hat{M F E}$ (hai góc tương ứng)

Mà hai góc này ở vị trí so le trong

Nên EF // DN

Lại có $\hat{D N A} = 90 °$ (chứng minh câu c) hay DN ⊥ NA.

Suy ra EF ⊥ NA (một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại).

Mặt khác EB ⊥ NA (giả thiết)

Suy ra ba điểm E, F, B cùng nằm trên một đường thẳng.

Vậy ba điểm E, F, B thẳng hàng.

Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:

SBT Toán 7 Bài 9 : Đường trung trực của một đoạn thẳng

SBT Toán 7 Bài 10 : Tính chất ba đường trung tuyến của tam giác

SBT Toán 7 Bài 11 : Tính chất ba đường phân giác của tam giác

SBT Toán 7 Bài 12 : Tính chất ba đường trung trực của tam giác

SBT Toán 7 Bài 13 : Tính chất ba đường cao của tam giác

Lý thuyết Tính chất ba đường trung tuyến của tam giác

1. Đường trung tuyến của tam giác

– Trong tam giác ABC (hình bên dưới), đoạn thẳng AM nối đỉnh A với trung điểm M của cạnh BC được gọi là đường trung tuyến (xuất phát từ đỉnh A hoặc tương ứng với cạnh BC).

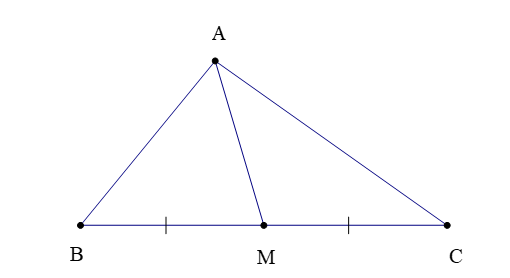
Tính chất ba đường trung tuyến của tam giác (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

Đôi khi, đường thẳng AM cũng được gọi là đường trung tuyến của ∆ABC.

Ví dụ: Quan sát hình bên dưới và cho biết trong hình có bao nhiêu đường trung tuyến?

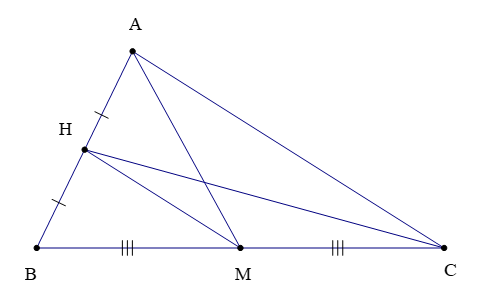
Tính chất ba đường trung tuyến của tam giác (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

Hướng dẫn giải

Quan sát hình vẽ ta có:

• A là đỉnh của ∆ABC và M là trung điểm của BC nên đoạn thẳng AM là đường trung tuyến của ∆ABC.

• C là đỉnh của ∆ABC và H là trung điểm của AB nên đoạn thẳng CH là đường trung tuyến của ∆ABC.

• M là đỉnh của ∆ABM và H là trung điểm của AB do đó MH là đường trung tuyến của ∆ABM.

• H là đỉnh của ∆HBC và M là trung điểm của BC nên đoạn thẳng HM là đường trung tuyến của ∆HBC.

Vậy trong hình vẽ trên có tất cả 4 đường trung tuyến.

– Chú ý: Mỗi tam giác có ba đường trung tuyến.

Ví dụ: Tam giác ABC (hình vẽ dưới) có ba đường trung tuyến là AM, BK và CN.

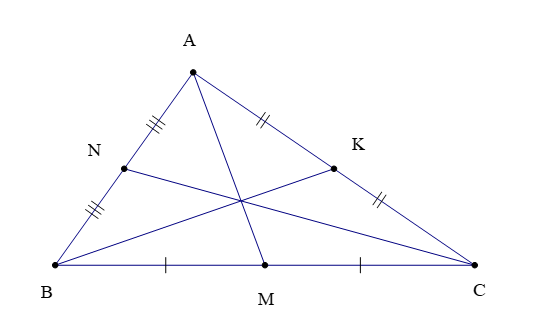
Tính chất ba đường trung tuyến của tam giác (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

2. Tính chất ba đường trung tuyến của tam giác

– Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm đó được gọi là trọng tâm của tam giác.

Chú ý: Trong tam giác ABC (hình vẽ dưới) có ba đường trung tuyến AM, BK, CN cùng đi qua điểm G, ta còn nói chúng đồng quy tại điểm G.

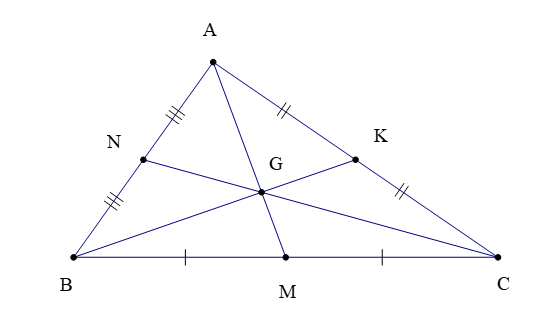
Tính chất ba đường trung tuyến của tam giác (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

Để xác định trọng tâm của một tam giác, ta chỉ cần vẽ hai đường trung tuyến bất kì và xác định giao điểm của hai đường đó.

Nhận xét: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng $\frac{2}{3}$ độ dài đường trung tuyến đi qua đỉnh ấy.

Lưu ý: Trong ∆ABC, với AM là đường trung tuyến và G là trọng tâm ta có:

$\frac{GM}{AM} = \frac{1}{3}, \frac{GM}{GA} = \frac{1}{2}$

Ví dụ: Cho ∆ABC như hình vẽ, biết AM = 18 cm và BN = 21 cm.

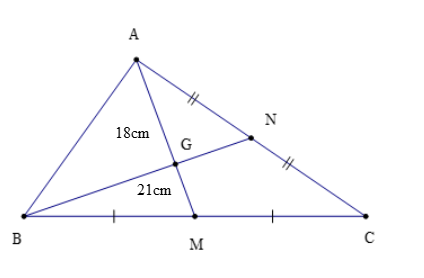
Tính chất ba đường trung tuyến của tam giác (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

a) Chứng minh: G là trọng tâm của ∆ABC.

b) Tính độ dài AG, GN.

Hướng dẫn giải

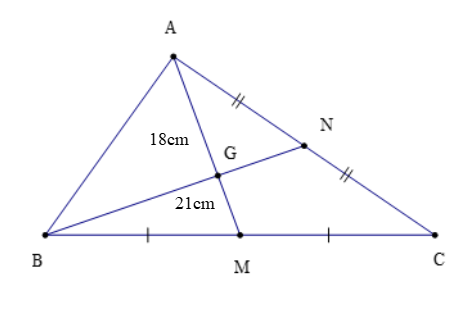
Tính chất ba đường trung tuyến của tam giác (Lý thuyết + Bài tập toán lớp 7) – Cánh diều (ảnh 1)

Theo hình vẽ trên ta có:

A là đỉnh của ∆ABC và M là trung điểm của BC nên đoạn thẳng AM là đường trung tuyến của ∆ABC.

B là đỉnh của ∆ABC và N là trung điểm của AC nên đoạn thẳng BN là đường trung tuyến của ∆ABC.

Mà hai đường trung tuyến AM và BN cắt nhau tại G do đó G là trọng tâm của ∆ABC.

Vậy G là trọng tâm của ∆ABC.

b) Theo phần a ta có: G là trọng tâm của ∆ABC nên $AG = \frac{2}{3} AM$ (tính chất trọng tâm của tam giác)

Hay $AG = \frac{2}{3} .18 = 12 (cm)$

Vì BN là đường trung tuyến của ∆ABC và G là trọng tâm của ∆ABC

Suy ra $\frac{GN}{BN} = \frac{1}{3}$ hay $GN = \frac{1}{3} BN = \frac{1}{3} .21 = 7 (cm)$

Vậy AG = 12 cm, GN = 7 cm.

Từ khóa :

Đánh giá

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Biết a - b chia hết cho 6 chứng minh rằng các biểu thức sau cũng chia hết cho 6 Lữ Ngọc My My

165

Toán Tổng hợp kiến thức

Tìm các tập hợp Ư(8); Ư(12); Ư(15) Lữ Ngọc My My

141

Toán Tổng hợp kiến thức

Tìm BCNN của 84 và 108 Lữ Ngọc My My

115

Toán Tổng hợp kiến thức

Cho biết cos∝ = 12/13 giá trị của tan ∝ là Lữ Ngọc My My

110

Tìm kiếm