Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 10 Bài 6: Hệ thức lượng trong tam giác chi tiết sách Toán 10 Tập 1 Kết nối tri thức với cuộc sống giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 6: Hệ thức lượng trong tam giác
Giải Toán 10 trang 38 Tập 1 Kết nối tri thức

Phương pháp giải:
Đánh dấu các vị trí, dùng thước thẳng để đo khảng cách và góc.
Lời giải:
Đặt cọc (vật cố định) tại vị trí đứng, kí hiệu là điểm A.
Di chuyển một đoạn d (m) đến vị trí B. Gọi C là vị trí của tháp Rùa.
Tại A và B xác định góc A và góc B của tam giác ABC.
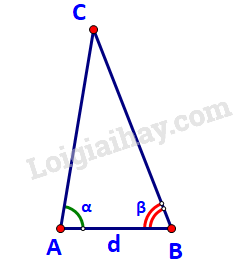
Áp dụng định lí sin trong tam giác ABC ta có:
Mà
1. Định lý côsin
a) Hãy vẽ sơ đồ đường đi của tàu trong 1,5 giờ kể từ khi xuất phát (1km trên thực tế ứng với 1 cm trên bản vẽ).
b) Hãy đo trực tiếp trên bản vẽ và cho biết sau 1,5 giờ kể từ khi xuất phát, tàu cách cảng Vân Phong bao nhiêu kilomet (số đo gần đúng).
c) Nếu sau khi đi được 2 giờ, tàu chuyển sang hướng nam (thay vì hướng đông nam) thì có thể dùng định lí Pythagore (Pi-ta-go) để tính chính xác các số đo trong câu b hay không?
Phương pháp giải:
a)
Bước 1: Xác định các hướng Đông, tây, nam, bắc. Giả sử tàu xuất phát từ điểm O.
Bước 2: Tính quãng đường đi theo từng hướng sau 1,5 giờ.
Bước 3: Vẽ sơ đồ đường đi
b)
Bước 1: Đo khoảng cách từ điểm xuất phát tới tàu trên sơ đồ
Bước 2: Quy ra khoảng cách thực tế.
c)
Bước 1: Vẽ sơ đồ đường đi.
Bước 2: Tính khoảng cách từ cảng tới tàu dựa vào định lí Pythagore.
Lời giải:
a) Giả sử tàu xuất phát từ điểm O như hình dưới.
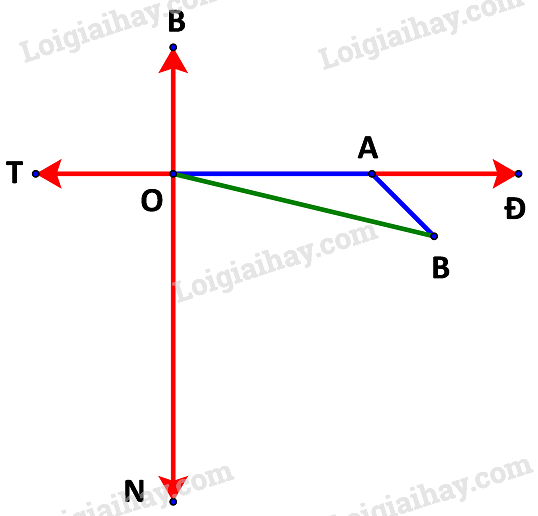
Trong 1 giờ, tàu di chuyển từ O đến A với quãng đường là: 20.1 =20 (km) tương ứng với 20 cm trên sơ đồ.
Trong 0,5 giờ tiếp theo, tàu di chuyển từ A đến B với quãng đường là: 20.0,5 = 10 (km) tương ứng với 10 cm trên sơ đồ.
b)
Trên sơ đồ, khoảng cách từ cảng đến tàu là đoạn OB dài khoảng 28 cm
Do đó khoảng cách từ cảng đến tàu thực tế khoảng 28 km.
c)
Nếu sau khi đi được 2 giờ, tàu chuyển sang hướng nam (thay vì hướng đông nam) thì sơ đồ đường đi của tàu như sau:
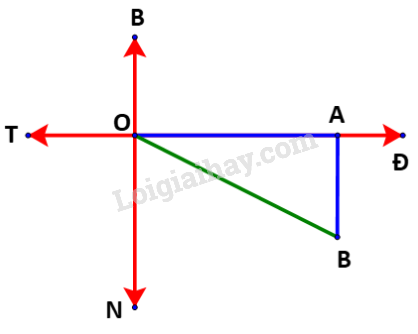
Sau 2 giờ đầu, tàu đi từ O đến A, với quãng đường là 20.2 = 40 (km) tương ứng 40 cm trên sơ đồ.
Sau đó, tàu chuyển sang hướng nam, vị trí của tàu là điểm B.
Khi đó ta có thể tính chính xác khoảng cách từ cảng đến tàu, chính là đoạn OB (do tam giác OAB vuông tại A) dựa vào định lí Pythagore:
a) Tính theo và
b) Tính theo b, c và DA.
c) Tính DA theo c và .
d) Chứng minh
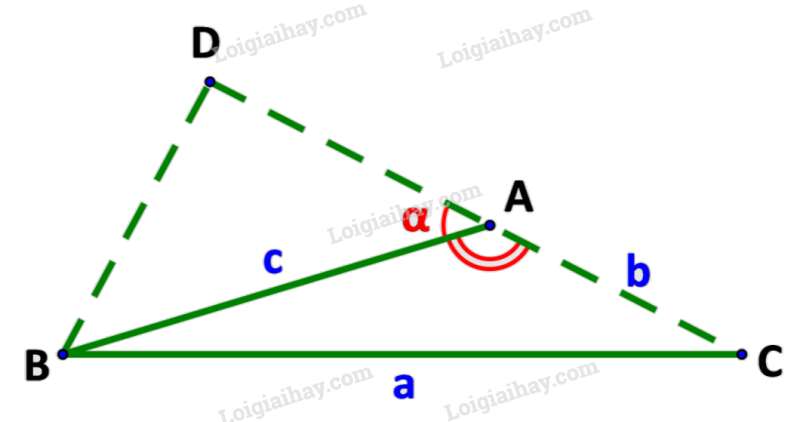
Phương pháp giải:
a) Áp dụng định lí Pythagore với tam giác BCD.
b) Bước 1: Tính BD theo DA và c (định lí Pythagore cho tam giác BDA)
Bước 2: Thay DC bởi DA + b.
Bước 3: Thế BD và DC ở trên vào biểu thức ở ý a)
c)
Bước 1: Tính theo .
Bước 2: Tính DA theo c và
Bước 3: Suy ra công thức tính DA theo c và
d)
Lời giải:
a) Xét tam giác BDC vuông tại D, theo định lý Pythagore ta có:
(1)
b) Xét tam giác vuông BDA ta có:
Lại có: DC = DA + AC = DA + b Thế vào (1)
(2)
c) Xét tam giác vuông BDA ta có:
Mà (do góc và góc A bù nhau)
d) Thế vào (2) ta được:
Giải Toán 10 trang 39 Tập 1 Kết nối tri thức
Lời giải:
Theo định lí cosin ta có:
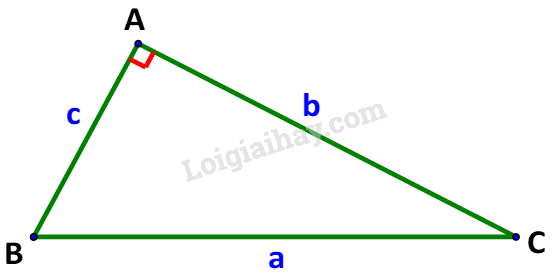
Mà
Vậy định lí Pythagore là một trường hợp đặc biệt của định lí cosin.
Phương pháp giải:
Từ định lí cosin cho tam giác ABC
Rút ra công thức tính cos A, cos B, cos C.
Lời giải:
Định lí cosin: Trong tam giác ABC
Ta có
Tương tự từ (2) và (3) ta suy ra ;
Phương pháp giải:
Bước 1: Tính cạnh BC (tương ứng là a) theo công thức
Bước 2: Tính cos B (theo công thức ) từ đó suy ra góc B.
Bước 3: Tính góc C.
Lời giải:
Áp dụng định lí cosin trong tam giác ABC
(trong đó: AB = c, BC = a và AC = b)
Ta được:
Từ (2) suy ra ;
Mà: a = BC =5,7; b =AC = 8; c =AB =5.
Vậy tam giác ABC có BC = 5,7,
Lời giải chi tiết:
Xét tam giác ABC như hình dưới:
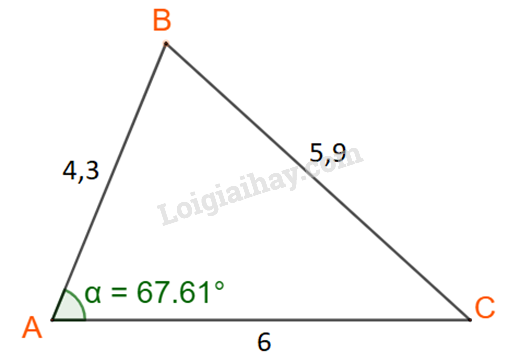
Áp dụng định lí cosin tại đỉnh A ta có:
Như vậy kết quả thu được từ định lí xấp xỉ với kết quả đo được.
Nói các khác định lí cosin tại đỉnh A là đúng.
Vận dụng 1 trang 39 Toán lớp 10: Dùng định lí cosin, tính khoảng cách được đề cập trong HĐ 1b.
Phương pháp giải:
Khoảng cách giữa tàu và cảng Vân Phong:
Lời giải:
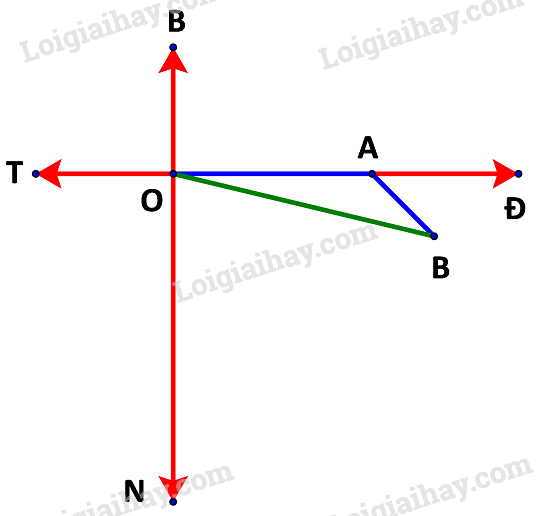
Tàu xuất phát từ cảng Vân Phong, đi theo thướng Đông với vận tốc 20km/h. Sau khi đi 1 giờ, tàu chuyển sang hướng đông nam rồi giữ nguyên vận tốc.
Giả sử sau 1,5 giờ tàu ở vị trí điểm B.
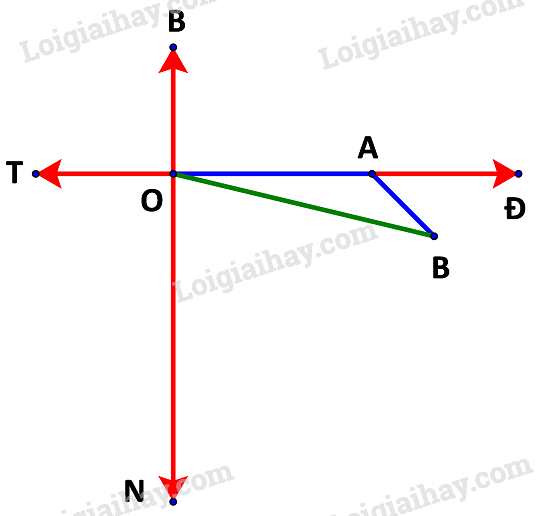
Ta đã có: quãng đường OA = 20 (km) và quãng đường AB =10 (km)
Ngoài ra (do tàu đi theo hướng đông nam)
Áp dụng định lí cosin tại đỉnh A ta được:
Vậy khoảng cách từ tàu tới cảng Vân Phong xấp xỉ 27,98 km.
2. Định lý sin
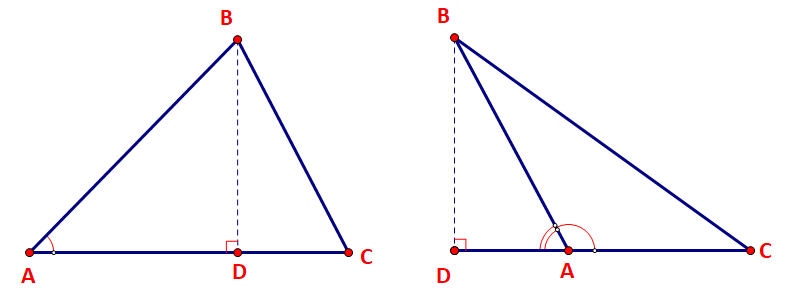
HĐ3 trang 39 Toán lớp 10: Trong mỗi hình dưới dây, hãy tính R theo a và sinA.
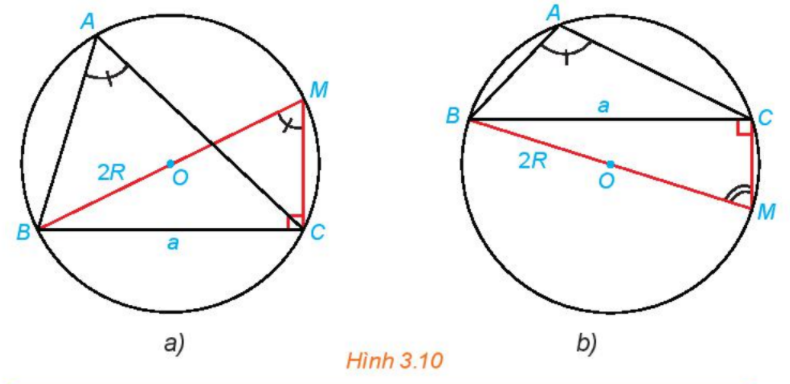
Phương pháp giải:
Bước 1: Tính sin M. Từ đó tính R theo a và sinM.
Bước 2: Tìm mối liên hệ giữa sinA và sinM, suy ra công thức tính R theo sinA.
Lời giải:
Xét tam giác MBC vuông tại C ta có:
Lại có: Hình 3.10 a: (cùng chắn cung nhỏ BC )
Hình 3.10b: (cùng tứ giác ABMC nội tiếp đường tròn (O,R))
Vậy ở cả hai hình ta đều có: .
Giải Toán 10 trang 40 Tập 1 Kết nối tri thức
Phương pháp giải:
Bước 1: Tính sin, bằng cách áp dụng định lí sin tại đỉnh B và C. Từ đó suy ra số đo góc C.
Bước 2: Tính và suy ra a dựa vào định lí sin.
Bước 3: Tính R.
Lời giải:
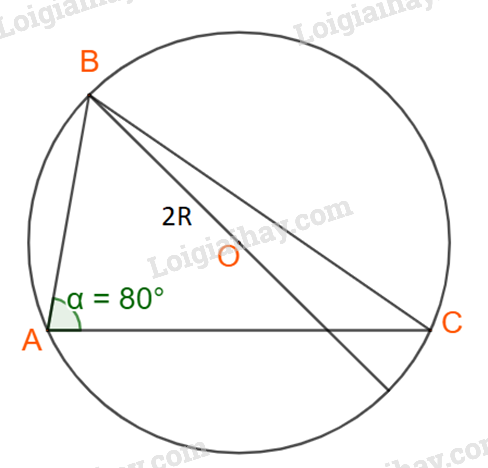
Áp dụng định lí sin cho tam giác ABC ta có:
Lại có:
Theo định lí sin, ta suy ra
Và
Vậy tam giác ABC có ; ; và
3. Giải tam giác và ứng dụng thực tế
Luyện tập 3 trang 40 Toán lớp 10: Giải tam giác ABC, biết b = 32, c =45,
Phương pháp giải:
Tính độ dài các cạnh và các góc còn lại của tam giác.
Bước 1: Tính a:
Bước 2: Tính sinB, suy ra góc B, góc C.
Lời giải:
Ta cần tính cạnh BC, góc B và góc C.
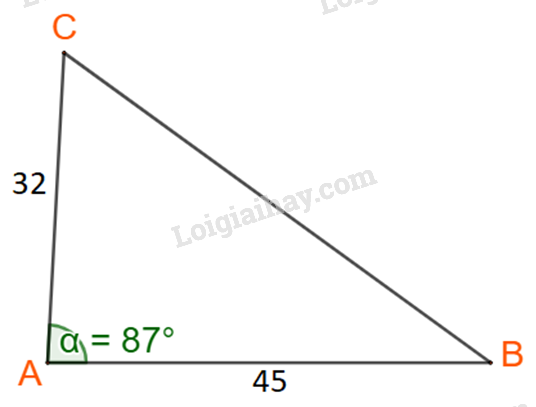
Áp dụng định lí cosin tại đỉnh A ta có:
Theo định lí sin, ta có:
hoặc (Loại vì )
Vậy tam giác ABC có ; và .
Phương pháp giải:
Bước 1: Cố định vị trí đứng ngắm, xác định góc ngắm .
Bước 2: Đo khoảng cách từ vị trí ngắm tới từng đỉnh núi..
Bước 3: Áp dụng định lí cosin để xác định khoảng cách giữa hai đỉnh núi.
Lời giải:
Bước 1: Tại khu vực quan sát, đặt một cọc tiêu cố định tại vị trí A. Kí hiệu hai đỉnh núi lần lượt là điểm B và điểm C.
+) Đứng tại A, ngắm điểm B và điểm C để đo góc tạo bởi hai hướng ngắm đó.
Bước 2: Đo khoảng cách từ vị trí ngắm đến từng đỉnh núi, tức là tính AB, AC.
+) Đứng tại A, ngắm đỉnh núi B để xác định góc ngắm so với mặt đất, kí hiệu là góc .
+) Theo hướng ngắm, đặt tiếp cọc tiêu tại D gần đỉnh núi hơn và đo đoạn AD. Xác định góc ngắm tại điểm D, kí hiệu là góc
Hình vẽ:
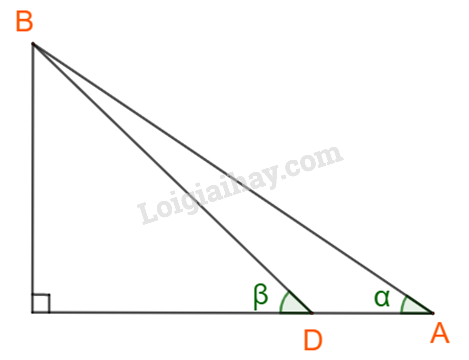
Dễ dàng tính được góc
Áp dụng định lí sin cho tam giác ABD ta được:
Bước 3: Tính khoảng cách giữa hai đỉnh núi, bằng cách áp dụng định lí cosin cho tam giác ABC để tính độ dài cạnh BC.
4. Công thức tính diện tích tam giác
Giải Toán 10 trang 41 Tập 1 Kết nối tri thức
HĐ4 trang 41 Toán lớp 10: Cho tam giác ABC với I là tâm đường trong nội tiếp tam giác.
a) Nêu mối liên hệ giữa diện tích tam giác ABC và diện tích các tam giác IBC, ICA, IAB.
b) Tính diện tích tam giác ABC theo r,a,b,c.
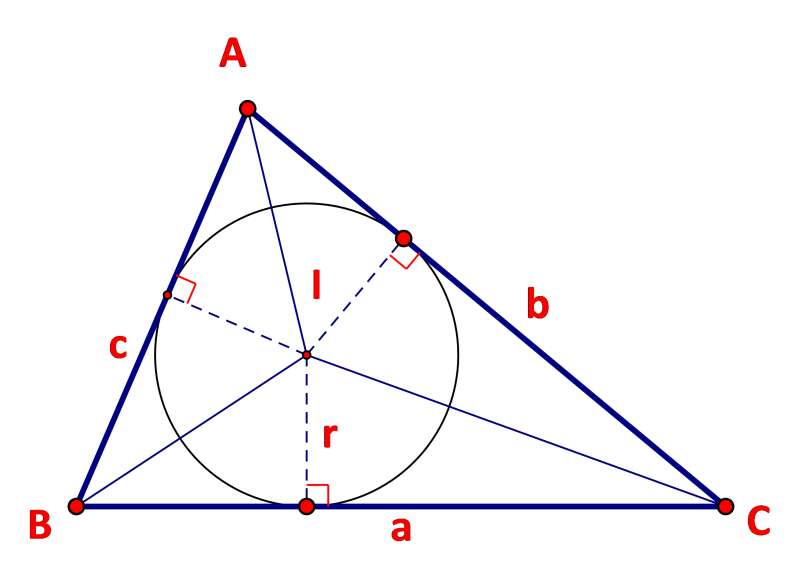
Phương pháp giải:
a) Tính diện tích tam giác ABC theo diện tích các tam giác IBC, ICA, IAB.
b) Diện tích tam giác IBC: .
Lời giải:
a) Diện tích tam giác ABC là:
b)
Kí hiệu: D,E, F lần lượt là hình chiếu của I trên AB, BC, AC.
Ta có:
Vậy diện tích tam giác ABC tính theo r, a, b, c là .
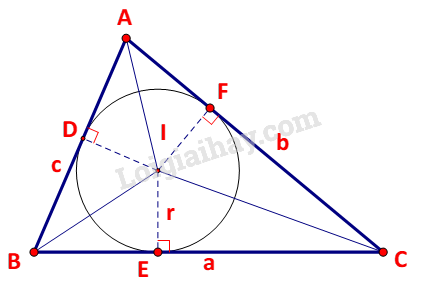
HĐ5 trang 41 Toán lớp 10: Cho tam giác ABC với đường cao BD.
a) Biểu thị BD theo AB và sinA.
b) Viết công thức tính diện tích S của tam giác ABC theo b,c, sin A.
Phương pháp giải:
a) Biểu thị BD dựa vào sin A (hoặc ) trong tam giác vuông ABD.
b)
+) Tính
+) Thay BD ở ý a) để suy ra công thức tính S theo b,c và sin A.
Lời giải:
a) Xét tam giác vuông ABD vuông tại D ta có:
TH1: góc A nhọn
TH2: góc A tù
Vậy
b) Ta có diện tích S của tam giác ABC là:
Mà ; BC = a. Thế vào (*) ta được:
hay
Vậy diện tích S của tam giác ABC theo b, c, sin A là
Luyện tập 4 trang 41 Toán lớp 10: Tính diện tích tam giác ABC có .
Phương pháp giải:
Bước 1: Tính c bằng cách áp dụng định lí sin.
Bước 2: Tính góc , tính
Lời giải:
Áp dụng định lí sin cho tam giác ABC ta có:
Lại có:
Do đó diện tích tích S của tam giác ABC là:
Vậy diện tích tam giác ABC là .
Phương pháp giải:
Nhắc lại:
+) công thức tính diện tích tam giác ABC:
+)
Bước 1: Tính sin A theo cos A. Lưu ý:
Bước 2: Thay sin A vào Rút gọn biểu thức rồi kết luận.
Lời giải:
Từ định lí cosin trong tam giác ABC, ta suy ra:
Mà
Do nên hay
Ta có:
Thế vào công thức tính diện tích tam giác ABC ta được:
Chú ý:
Nếu tiếp tục biến đổi công thức diện tích ta được
Đến đây, đặt , là nửa chu vi tam giác ABC, ta suy ra:
Giải Toán 10 trang 42 Tập 1 Kết nối tri thức
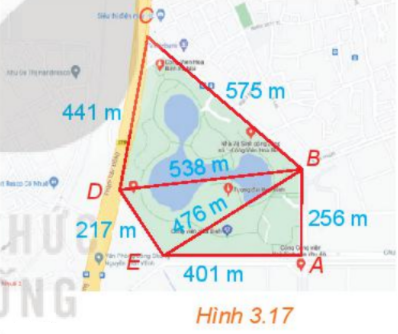
Phương pháp giải:
Bước 1: Tính diện tích các tam giác CBD, DBE, EBA bằng công thức Herong:
Bước 2: Tính diện tích ngũ giác ABCDE, bằng tổng diện tích các tam giác CBD, DBE, EBA.
Lời giải:
Xét tam giác CDB, ta có: CD = 441, CB = 575 và DB = 538 (đơn vị: m)
Và nửa chu vi là:
Do đó:
Xét tam giác DBE, ta có: DE = 217, EB = 476 và DB = 538 (đơn vị: m)
Và nửa chu vi là:
Do đó:
Xét tam giác ABE, ta có: AE = 401, EB = 476 và BA =256 (đơn vị: m)
Và nửa chu vi là:
Do đó:
Vậy diện tích S của ngũ giác ABCDE là:
Chú ý
+) Để tính diện tích ngũ giác ABCDE thông qua các tam giác nhỏ, ta cần chọn các tam giác thỏa mãn: “phần trong của chúng không đè lên nhau” và “ghép lại vừa khít tạo thành ngũ giác ABCDE”
+) Ưu tiên tính thông qua các tam giác đã biết đủ các cạnh.
Bài tập
Bài 3.5 trang 42 Toán lớp 10: Cho tam giác ABC có a = 6, b = 5, c =8. Tính cos A, S,r.
Phương pháp giải:
Bước 1: Tính cos A bằng công thức:
Bước 2: Tính S bằng công thức Herong: với
Bước 3: Tính r bằng công thức .
Lời giải:
Từ định lí cosin ta suy ra
Tam giác ABC có nửa chu vi là:
Theo công thức Herong ta có:
Lại có:
Vậy ; và
Bài 3.6 trang 42 Toán lớp 10: Cho tam giác ABC có . Tính R,b,c.
Phương pháp giải:
Bước 1: Tính R và b bằng định lí sin:
Bước 2: Tính và suy ra c bằng định lí sin.
Lời giải:
Áp dụng định lí sin trong tam giác ABC ta có:
Mà
Mặt khác:
Từ định lí sin ta suy ra:
Vậy ;
Bài 3.7 trang 42 Toán lớp 10: Giải tam giác ABC và tính diện tích của tam giác đó, biết .
Phương pháp giải:
Tính a, b, và S
Bước 1: Tính rồi suy ra a, b bằng định lí sin:
Bước 2: Tính .
Lời giải:
Ta có:
Áp dụng định lí sin trong tam giác ABC ta có:
Mà
Diện tích tam giác ABC là
Vậy ; ;
a) Tính khoảng cách từ cảng A tới đảo nơi tàu neo đậu.
b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu.
a,
Tính khoảng cách từ cảng A tới đảo nơi tàu neo đậu
Phương pháp giải:
Bước 1: Vẽ hình mô tả đường đi từ cảng A, đến nơi mà động cơ hỏng (kí hiệu là B) và hòn đảo (kí hiệu là C) nơi tàu neo đậu.
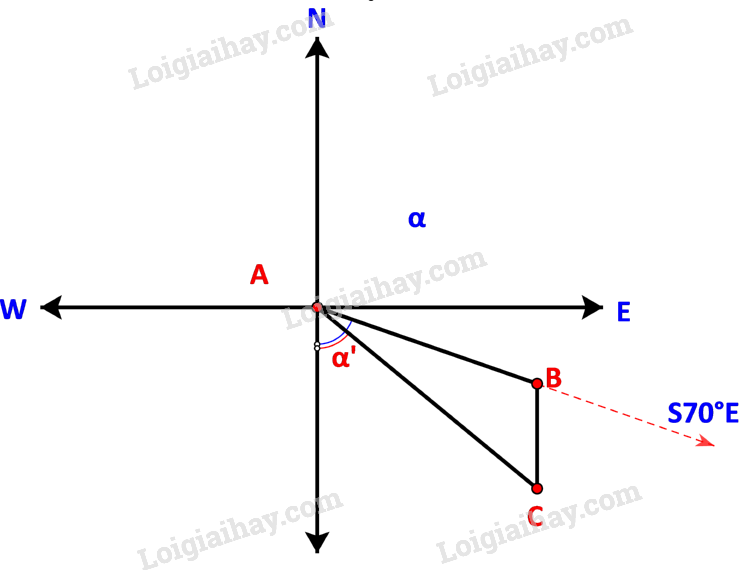
Bước 2: Tính góc , quãng đường tàu đi được sau 90 phút () và quãng đường tàu trôi tự do ().
Bước 3: Tính khoảng cách từ cảng tới nơi tàu neo đậu (đoạn AC) bằng cách áp dụng định lí cosin tại đỉnh B.
Lời giải:
Ta có sơ đồ đường đi như sau:
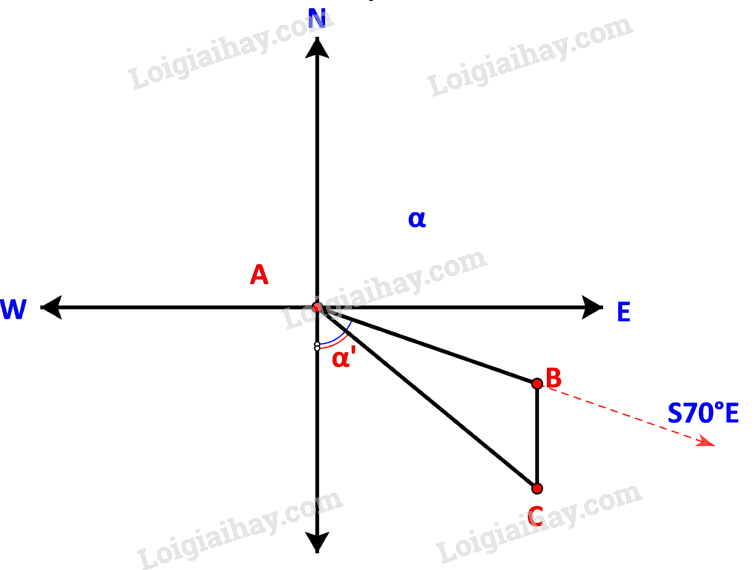
Trong đó: B là nơi động cơ bị hỏng, C là ví trí neo đậu của tàu trên hòn đảo.
Khoảng cách từ cảng A tới đảo nơi tàu neo đậu là đoạn AC (hay b).
Ban đầu tàu di chuyển theo hướng nên . Sau khi động cơ bị hỏng, tàu trôi theo hướng Nam do đó BC song song với AS.
Quãng đường tàu đi được sau 90 phút hay 1,5 giờ (ngay trước khi hỏng động cơ) là:
70.1,5 = 105 (km) hay c = 105.
Quãng đường tàu trôi tự do là:
8.2 = 16 (km) hay a = 16.
Áp dụng định lí cosin cho tam giác ABC ta có:
Vậy khoảng cách từ cảng A tới đảo nơi tàu neo đậu là khoảng 110,23 km.
b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu.
Phương pháp giải:
Bước 1: Trên sơ đồ: xác định góc nào là hướng từ cảng A tới đảo nơi tàu neo đậu.
Bước 2: Tính sin dựa vào định lí sin
Bước 3: Suy ra góc cần tính và kết luận.
Lời giải:
Theo sơ đồ, hướng từ cảng A tới đảo nơi tàu neo đậu là với .
Áp dụng định lí sin cho tam giác ABC ta có:
Mà ; ; a = 16.
Vậy hướng từ cảng A tới đảo nơi tàu neo đậu là .
a) Tính các góc của tam giác ABC.
b) Tính chiều cao của tòa nhà.
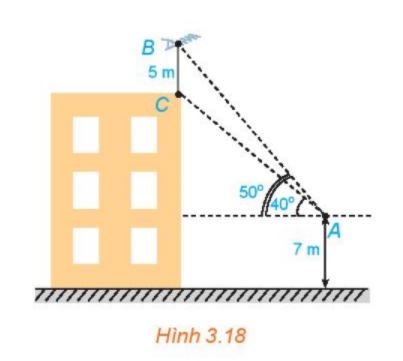
a) Tính các góc của tam giác ABC.
Phương pháp giải:
Nhắc lại: Tổng ba góc của một tam giác luôn bằng .
Bước 1: Gọi H là hình chiếu của A lên đường thẳng BC.
Bước 2: Tính góc , góc => góc .
Lời giải:
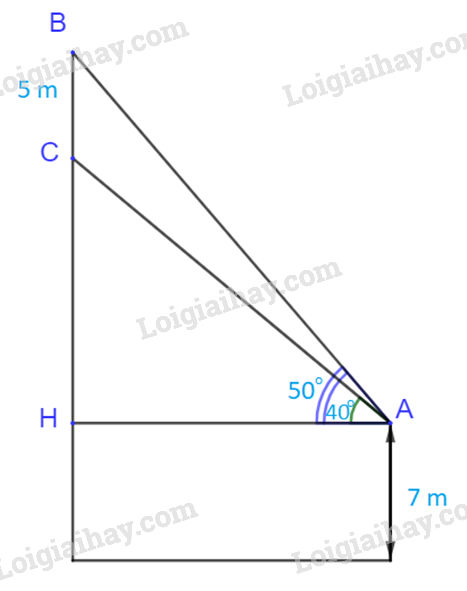
Gọi H là hình chiếu của A lên đường thẳng BC.
Ta có: ;
(1)
Xét tam giác ABH, vuông tại H ta có:
hay . (2)
Từ (1) và (2), suy ra:
Vậy ba góc của tam giác ABC lần lượt là: .
b) Tính chiều cao của tòa nhà.
Phương pháp giải:
Bước 1: Tính AB:
Bước 2: Tính BH => chiều cao của tòa nhà = BH + độ cao của vị trí quan sát.
Lời giải:
Áp dụng định lý sin cho tam giác ABC, ta được:
Mà:
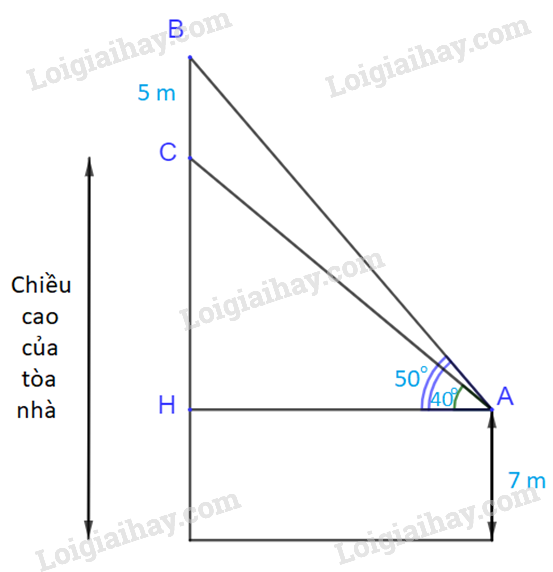
Xét tam giác ABH, vuông tại H ta có:
Mà:
Vậy chiều cao của tòa nhà là:

Lời giải:
Bước 1:
Đánh dấu vị trí quan sát tại điểm A, chiều rộng của hòn đảo kí hiệu là đoạn BC.
Gọi H là hình chiếu của A trên BC.
Trên tia đối của tia AH, lấy điểm M, ghi lại khoảng cách AM = a.
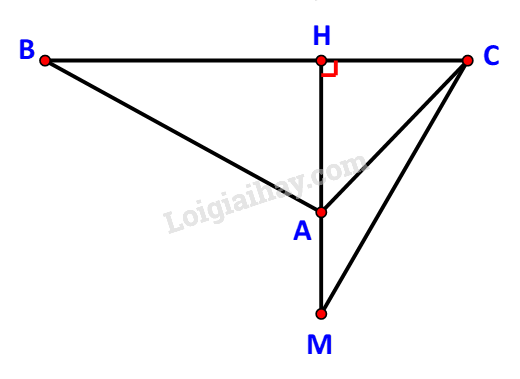
Bước 2:
Tại A, quan sát để xác định các góc .
Tiếp tục quan sát tại M, xác định góc .
Bước 3: Giải tam giác AMC, tính AC.
AM = a, và
Áp dụng định định lí sin trong tam giác AMC ta có:
Bước 4:
Áp dụng định lí sin cho tam giác ABC ta có:
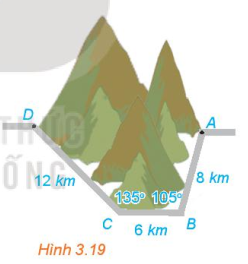
Phương pháp giải:
Bước 1: Tính AC:
Bước 2: Tính góc ACB, suy ra góc ACD.
Bước 3: Tính AD:
Bước 4: Tính số kilomet giảm đi so với đường cũ.
Lời giải:
Bước 1:
Áp dụng định lí cos trong tam giác ABC ta có:
Bước 2:
Lại có: Theo định lí sin thì
Bước 3:
Áp dụng định lí cos trong tam giác ACD ta có:
Bước 4:
Độ dài đường mới giảm số kilomet so với đường cũ là:
Lý thuyết Hệ thức lượng trong tam giác
1. Định lí Côsin
Đối với tam giác ABC, ta thường kí hiệu A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.
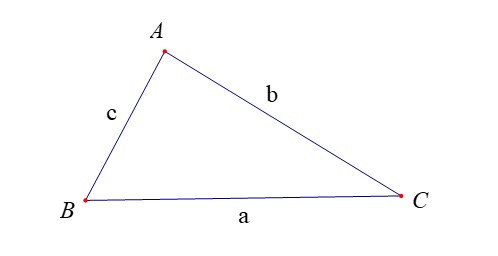
Định lí Côsin. Trong tam giác ABC:
a2 = b2 + c2 – 2bc.cosA.
b2 = c2 + a2 – 2ca.cosB.
c2 = a2 + b2 – 2ab.cosC.
Ví dụ: Cho tam giác ABC có góc A bằng 60° và AB = 2 cm, AC = 3 cm. Tính độ dài cạnh BC.
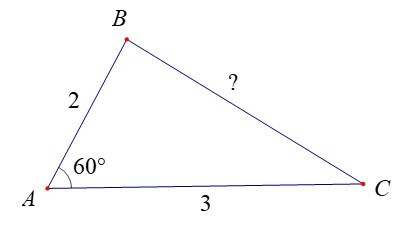
Hướng dẫn giải
Áp dụng Định lí côsin cho tam giác ABC, ta có:
BC2 = AB2 + AC2 – 2AB . AC . cos 60o = 22 + 32 – 2.2.3. = 7.
Suy ra BC = (cm)
Vậy BC = cm.
2. Định lí sin
Trong tam giác ABC: .
Ví dụ: Cho tam giác ABC có , , c = 10. Tính số đo góc C và a, b, R.
Hướng dẫn giải
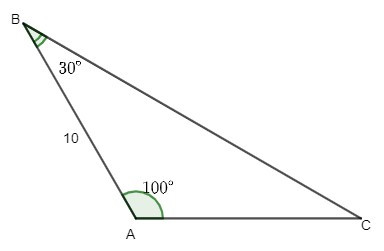
Theo Định lí tổng ba góc của tam giác, ta có: .
Suy ra .
Áp dụng Định lí sin, ta có:
.
Suy ra:
.
Vậy a = ; b = 10; R = 10; .
3. Giải tam giác và ứng dụng thực tế
- Việc tính độ dài các cạnh và số đo các góc của một tam giác khi biết một số yếu tố của tam giác đó được gọi là giải tam giác.
Chú ý: Áp dụng định lí côsin, sin và sử dụng máy tính cầm tay, ta có thể tính (gần đúng) các cạnh và các góc của một tam giác trong các trường hợp sau:
+ Biết hai cạnh và góc xen giữa.
+ Biết ba cạnh.
+ Biết một cạnh và hai góc kề.
Ví dụ: Giải tam giác ABC biết b = 12, , .
Hướng dẫn giải
Theo định lí tổng ba góc của tam giác, ta có: .
Suy ra .
Áp dụng định lí sin, ta có:
Suy ra:
Vậy tam giác ABC có: , , ; a ≈ 34,6 ; b = 12; c ≈ 30,4.
Ví dụ: Để đo khoảng cách giữa hai đầu C và A của một hồ nước người ta không thể đi trực tiếp từ C đến A, người ta tiến hành như sau: Chọn 1 điểm B sao cho đo được khoảng cách BC, BA và góc BCA. Sau khi đo, ta nhận được BC = 5m, BA = 12m, . Tính khoảng cách AC (làm tròn kết quả đến hàng phần trăm).
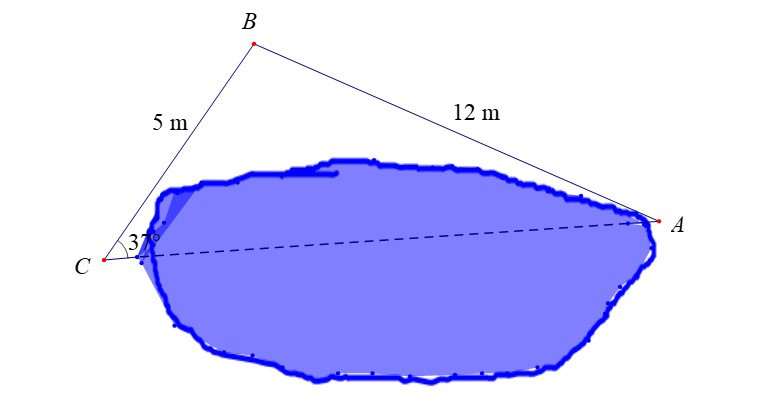
Hướng dẫn giải
Áp dụng định lí sin đối với tam giác ABC ta có:
⇒
⇒ sin A =
⇒ ≈ 14°31’
⇒ ≈ 180° – (37° + 14°31’) = 128°29’.
Áp dụng định lí sin, ta có:
⇒ AC = = ≈15,61 (m)
Vậy khoảng cách AC ≈ 15,61 m.
4. Công thức tính diện tích tam giác
Đối với tam giác ABC: A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.
Ta có các công thức tính diện tích tam giác ABC sau:
+) S = pr =
+) S = bc sin A = ca sin B =ab sin C.
+) S =
+) Công thức Heron: S = .
Ví dụ:
a) Tính diện tích tam giác ABC biết các cạnh b = 14 cm, c = 35 cm và .
b) Tính diện tích tam giác ABC và bán kính đường tròn nội tiếp, ngoại tiếp tam giác ABC, biết các cạnh a = 4 cm, b = 5 cm, c = 3 cm.
Hướng dẫn giải
a) Áp dụng công thức tính diện tích tam giác ABC, ta có:
S = bc sin A = .14.35.sin 60° = .14.35.=(cm2).
Vậy diện tích tam giác ABC là: cm2.
b) Ta có nửa chu vi của tam giác ABC là: (cm).
Áp dụng công thức Heron, ta có diện tích tam giác ABC là:
S = (cm2).
Mặt khác: S = ⇒ R = = (cm).
Ta có: S = pr ⇒ r = = = 1 (cm).
Vậy diện tích tam giác ABC là 6 cm2, bán kính đường tròn ngoại tiếp là 2,5 cm; bán kính đường tròn nội tiếp là 1 cm.
Xem thêm các bài giải SGK Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 5: Giá trị lượng giác của một góc từ 0 đến 180
Bài 8: Tổng và hiệu của hai vectơ