Với giải Vận dụng 2 trang 40 Toán lớp 10 Kết nối tri thức với cuộc sống trong Bài 6: Hệ thức lượng trong tam giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 6: Hệ thức lượng trong tam giác
Vận dụng 2 trang 40 Toán lớp 10: Từ một khu vực có thể quan sát được hai đỉnh núi, ta có thể ngắm và đo để xác định khoảng cách giữa hai đỉnh núi đó. Hãy thảo luận để đưa ra các bước cho một cách đo.
Phương pháp giải:
Bước 1: Cố định vị trí đứng ngắm, xác định góc ngắm .
Bước 2: Đo khoảng cách từ vị trí ngắm tới từng đỉnh núi..
Bước 3: Áp dụng định lí cosin để xác định khoảng cách giữa hai đỉnh núi.
Lời giải:
Bước 1: Tại khu vực quan sát, đặt một cọc tiêu cố định tại vị trí A. Kí hiệu hai đỉnh núi lần lượt là điểm B và điểm C.
+) Đứng tại A, ngắm điểm B và điểm C để đo góc tạo bởi hai hướng ngắm đó.
Bước 2: Đo khoảng cách từ vị trí ngắm đến từng đỉnh núi, tức là tính AB, AC.
+) Đứng tại A, ngắm đỉnh núi B để xác định góc ngắm so với mặt đất, kí hiệu là góc .
+) Theo hướng ngắm, đặt tiếp cọc tiêu tại D gần đỉnh núi hơn và đo đoạn AD. Xác định góc ngắm tại điểm D, kí hiệu là góc
Hình vẽ:
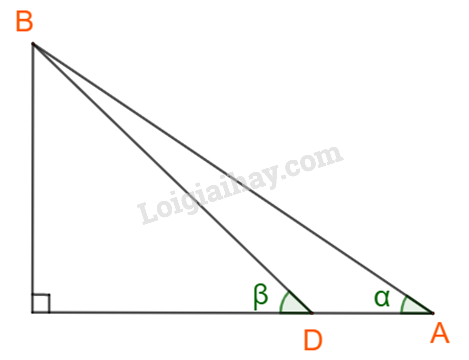
Dễ dàng tính được góc
Áp dụng định lí sin cho tam giác ABD ta được:
Bước 3: Tính khoảng cách giữa hai đỉnh núi, bằng cách áp dụng định lí cosin cho tam giác ABC để tính độ dài cạnh BC.
Lý thuyết Giải tam giác và ứng dụng thực tế
- Việc tính độ dài các cạnh và số đo các góc của một tam giác khi biết một số yếu tố của tam giác đó được gọi là giải tam giác.
Chú ý: Áp dụng định lí côsin, sin và sử dụng máy tính cầm tay, ta có thể tính (gần đúng) các cạnh và các góc của một tam giác trong các trường hợp sau:
+ Biết hai cạnh và góc xen giữa.
+ Biết ba cạnh.
+ Biết một cạnh và hai góc kề.
Ví dụ: Giải tam giác ABC biết b = 12, , .
Hướng dẫn giải
Theo định lí tổng ba góc của tam giác, ta có: .
Suy ra .
Áp dụng định lí sin, ta có:
Suy ra:
Vậy tam giác ABC có: , , ; a ≈ 34,6 ; b = 12; c ≈ 30,4.
Ví dụ: Để đo khoảng cách giữa hai đầu C và A của một hồ nước người ta không thể đi trực tiếp từ C đến A, người ta tiến hành như sau: Chọn 1 điểm B sao cho đo được khoảng cách BC, BA và góc BCA. Sau khi đo, ta nhận được BC = 5m, BA = 12m, . Tính khoảng cách AC (làm tròn kết quả đến hàng phần trăm).
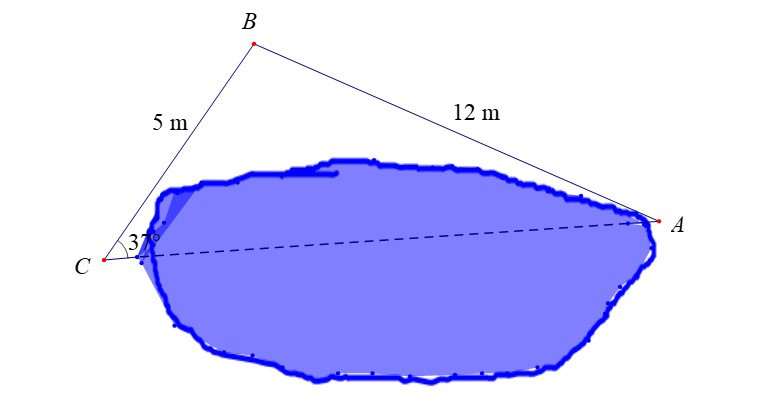
Hướng dẫn giải
Áp dụng định lí sin đối với tam giác ABC ta có:
⇒
⇒ sin A =
⇒ ≈ 14°31’
⇒ ≈ 180° – (37° + 14°31’) = 128°29’.
Áp dụng định lí sin, ta có:
⇒ AC = = ≈15,61 (m)
Vậy khoảng cách AC ≈ 15,61 m.
Xem thêm các bài giải Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:
Vận dụng 1 trang 39 Toán lớp 10: Dùng định lí cosin, tính khoảng cách được đề cập trong HĐ 1b...
HĐ3 trang 39 Toán lớp 10: Trong mỗi hình dưới dây, hãy tính R theo a và sinA...
Luyện tập 3 trang 40 Toán lớp 10: Giải tam giác ABC, biết b = 32, c =45, ...
HĐ4 trang 41 Toán lớp 10: Cho tam giác ABC với I là tâm đường trong nội tiếp tam giác...
HĐ5 trang 41 Toán lớp 10: Cho tam giác ABC với đường cao BD...
Luyện tập 4 trang 41 Toán lớp 10: Tính diện tích tam giác ABC có ...
Bài 3.5 trang 42 Toán lớp 10: Cho tam giác ABC có a = 6, b = 5, c =8. Tính cos A, S,r...
Bài 3.6 trang 42 Toán lớp 10: Cho tam giác ABC có . Tính R,b,c...
Bài 3.7 trang 42 Toán lớp 10: Giải tam giác ABC và tính diện tích của tam giác đó, biết ...
Xem thêm các bài giải SGK Toán 10 Kết nối tri thức hay, chi tiết khác:
Bài 5: Giá trị lượng giác của một góc từ 0 đến 180
Bài 6: Hệ thức lượng trong tam giác
Bài 8: Tổng và hiệu của hai vectơ