Câu hỏi trang 39 Toán lớp 10: Định lí Pythagore có phải là một trường hợp đặc biệt của định lí cosin hay không?

Lời giải:

Theo định lí cosin ta có:

$\begin{array}{l}{a}^2=b^2+c^2-2bc.\cos A\\ b^2=a^2+c^2-2ac.\cos B\\ c^2=b^2+a^2-2ab.\cos C\end{array}$

Mà $\cos A=\cos {90}^o=0;\cos B=\frac{c}{a};\cos C=\frac{b}{a}$

 $\Rightarrow \{\begin{array}{l}{a}^2=b^2+c^2-2bc.0\\ b^2=a^2+c^2-2ac.\frac{c}{a}\\ c^2=b^2+a^2-2ab.\frac{b}{a}\end{array}$$\iff \{\begin{array}{l}{a}^2=b^2+c^2\\ b^2=a^2+c^2-2a^2\\ c^2=b^2+a^2-2b^2\end{array}\iff a^2=b^2+c^2$

Vậy định lí Pythagore là một trường hợp đặc biệt của định lí cosin.

Khám phá trang 39 Toán lớp 10: Từ định lí cosin hãy viết các công thức tính cos A, cos B, cos C theo độ dài các cạnh a, b, c của tam giác ABC.

Phương pháp giải:

Từ định lí cosin cho tam giác ABC

$\begin{array}{l}{a}^2=b^2+c^2-2bc.\cos A\\ b^2=a^2+c^2-2ac.\cos B\\ c^2=b^2+a^2-2ab.\cos C\end{array}$

Rút ra công thức tính cos A, cos B, cos C.

Lời giải:

Định lí cosin: Trong tam giác ABC

$\begin{array}{l}{a}^2=b^2+c^2-2bc.\cos A(1)\\ b^2=a^2+c^2-2ac.\cos B(2)\\ c^2=b^2+a^2-2ab.\cos C(3)\end{array}$

Ta có $(1)\iff 2bc\cos A=b^2+c^2-a^2\iff \cos A=\frac{b^2+c^2-a^2}{2bc}.$

Tương tự từ (2) và (3) ta suy ra $\cos B=\frac{a^2+c^2-b^2}{2ac}$; $\cos C=\frac{b^2+a^2-c^2}{2ba}$

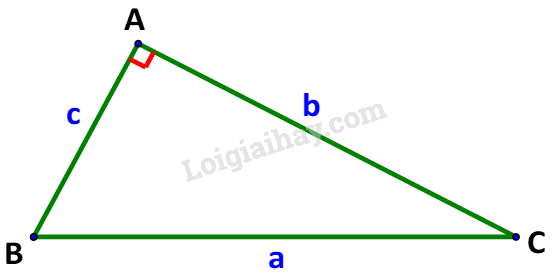
Luyện tập 1 trang 39 Toán lớp 10: Cho tam giác ABC có AB = 5, AC = 8 và $\hat{A}={45}^o$. Tính độ dài các cạnh và độ lớn các góc còn lại của tam giác.

Phương pháp giải:

Bước 1: Tính cạnh BC (tương ứng là a) theo công thức $a^2=b^2+c^2-2bc.\cos A$

Bước 2: Tính cos B (theo công thức $\cos B=\frac{a^2+c^2-b^2}{2ac}$) từ đó suy ra góc B.

Bước 3: Tính góc C.

Lời giải:

Áp dụng định lí cosin trong tam giác ABC

$\begin{array}{l}{a}^2=b^2+c^2-2bc.\cos A(1)\\ b^2=a^2+c^2-2ac.\cos B(2)\end{array}$

(trong đó: AB = c, BC = a và AC = b)

Ta được:  $B{C}^2=a^2=8^2+5^2-\mathrm{2.8.5.}\cos {45}^o=89-40\sqrt{2}$$\Rightarrow BC\approx 5,7$

Từ (2) suy ra $\cos B=\frac{a^2+c^2-b^2}{2ac}$;

Mà: a = BC =5,7; b =AC = 8; c =AB =5.

$\Rightarrow \cos B\approx \frac{-217}{1900}\Rightarrow \hat{B}\approx {97}^o\Rightarrow \hat{C}\approx {38}^o$

Vậy tam giác ABC có BC = 5,7, $\hat{B}={97}^o,\hat{C}={38}^o$

Trải nghiệm trang 39 Toán lớp 10: Vẽ một tam giác ABC, sau đó đo độ dài các cạnh, số đo góc A và kiểm tra tính đúng đắn của Định lí cosin tại đỉnh A đối với tam giác đó.

Lời giải chi tiết:

Xét tam giác ABC như hình dưới:

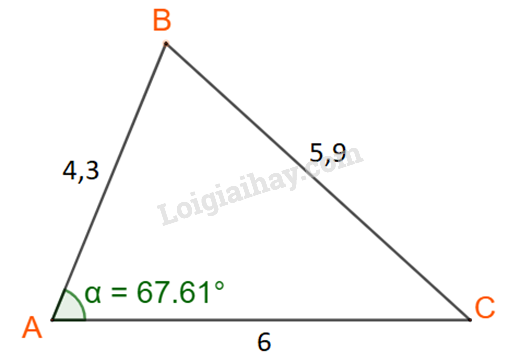
Áp dụng định lí cosin tại đỉnh A ta có:

$a^2=b^2+c^2-2bc.\cos A$

$\begin{array}{l}\iff B{C}^2=6^2+4,3^2-\mathrm{2.6.4},3.\cos 67,{61}^o\\ \iff B{C}^2\approx 34,835\\ \iff BC\approx 5,9\end{array}$

Như vậy kết quả thu được từ định lí xấp xỉ với kết quả đo được.

Nói các khác định lí cosin tại đỉnh A là đúng.

Vận dụng 1 trang 39 Toán lớp 10: Dùng định lí cosin, tính khoảng cách được đề cập trong HĐ 1b.

Phương pháp giải:

Khoảng cách giữa tàu và cảng Vân Phong: $O{B}^2=O{A}^2+A{B}^2-2.OA.AB.\cos \widehat{OAB}$

Lời giải:

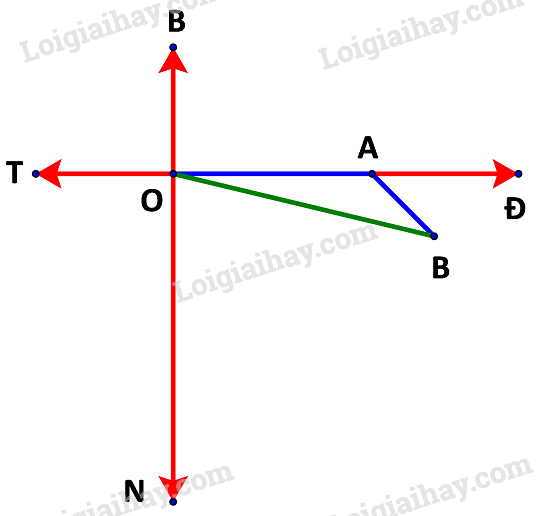
Tàu xuất phát từ cảng Vân Phong, đi theo thướng Đông với vận tốc 20km/h. Sau khi đi 1 giờ, tàu chuyển sang hướng đông nam rồi giữ nguyên vận tốc.

Giả sử sau 1,5 giờ tàu ở vị trí điểm B.

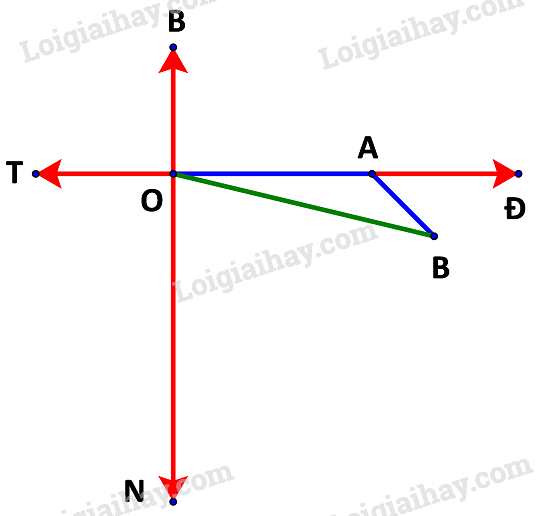
Ta đã có: quãng đường OA = 20 (km) và quãng đường AB =10 (km)

Ngoài ra $\widehat{OAB}={135}^o$ (do tàu đi theo hướng đông nam)

Áp dụng định lí cosin tại đỉnh A ta được:

 $O{B}^2=O{A}^2+A{B}^2-2.OA.AB.\cos \widehat{OAB}$

$\begin{array}{l}\iff O{B}^2={20}^2+{10}^2-\mathrm{2.20.10.}\cos {135}^o\\ \iff O{B}^2\approx 782,84\\ \iff OB\approx 27,98.\end{array}$

Vậy khoảng cách từ tàu tới cảng Vân Phong xấp xỉ 27,98 km.

2. Định lý sin

HĐ3 trang 39 Toán lớp 10: Trong mỗi hình dưới dây, hãy tính R theo a và sinA.

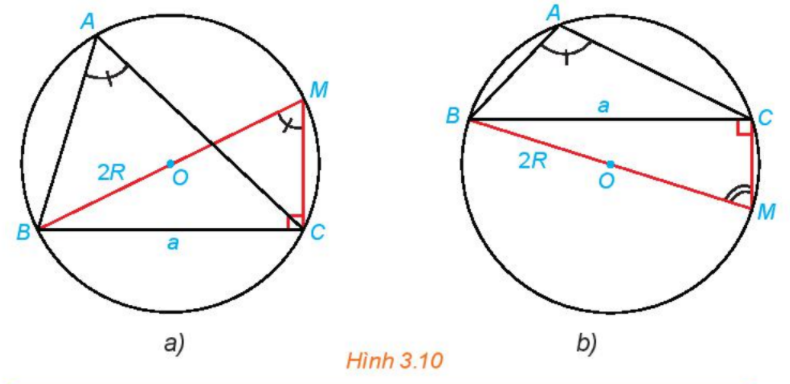
Phương pháp giải:

Bước 1: Tính sin M. Từ đó tính R theo a và sinM.

Bước 2: Tìm mối liên hệ giữa sinA và sinM, suy ra công thức tính R theo sinA.

Lời giải:

 Xét tam giác MBC vuông tại C ta có:

$\sin M={\displaystyle \frac{BC}{BM}}={\displaystyle \frac{a}{2R}}\Rightarrow R={\displaystyle \frac{a}{2\sin M}}$

Lại có: Hình 3.10 a:  $\hat{A}=\hat{M}$ (cùng chắn cung nhỏ BC )

$\Rightarrow \sin A=\sin M\Rightarrow R={\displaystyle \frac{a}{2\sin A}}$

Hình 3.10b: $\hat{A}+\hat{M}={180}^o$ (cùng tứ giác ABMC nội tiếp đường tròn (O,R))

$\Rightarrow \sin A=\sin M\Rightarrow R={\displaystyle \frac{a}{2\sin A}}$

Vậy ở cả hai hình ta đều có: $R={\displaystyle \frac{a}{2\sin A}}$.

Xem thêm lời giải Toán 10 Kết nối tri thức hay, chi tiết khác:

Giải Toán 10 trang 38 Tập 1 

Giải Toán 10 trang 39 Tập 1 

Giải Toán 10 trang 40 Tập 1 

Giải Toán 10 trang 41 Tập 1 

Giải Toán 10 trang 42 Tập 1