Bài 3.9 trang 43 Toán 10 tập 1 | Kết nối tri thức Giải Toán lớp 10

Thảo Ngày: 23-08-2024 Lớp 10

5.3 K

Với giải Bài 3.9 trang 43 Toán lớp 10 Kết nối tri thức với cuộc sống trong Bài 6: Hệ thức lượng trong tam giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 6: Hệ thức lượng trong tam giác

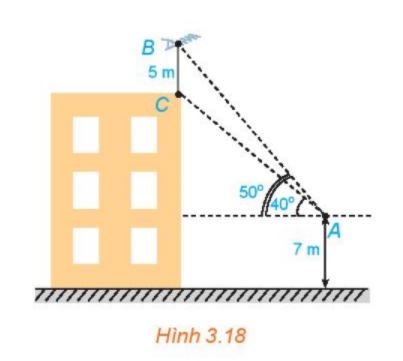
Bài 3.9 trang 43 Toán lớp 10: Trên nóc một tòa nhà có một cột ăng-ten cao 5m. Từ một vị trí quan sát A cao 7 m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng-ten, với các góc tương ứng là $50^{o}$ và $40^{o}$ so với phương nằm ngang (H.3.18).

a) Tính các góc của tam giác ABC.

b) Tính chiều cao của tòa nhà.

Bài 3.8 trang 42 Toán lớp 10 Tập 1 | Kết nối tri thức (ảnh 1)

a) Tính các góc của tam giác ABC.

Phương pháp giải:

Nhắc lại: Tổng ba góc của một tam giác luôn bằng $180^{o}$ .

Bước 1: Gọi H là hình chiếu của A lên đường thẳng BC.

Bước 2: Tính góc $\hat{B A C}$ , góc $\hat{A B C}$ => góc $\hat{B C A}$ .

Lời giải:

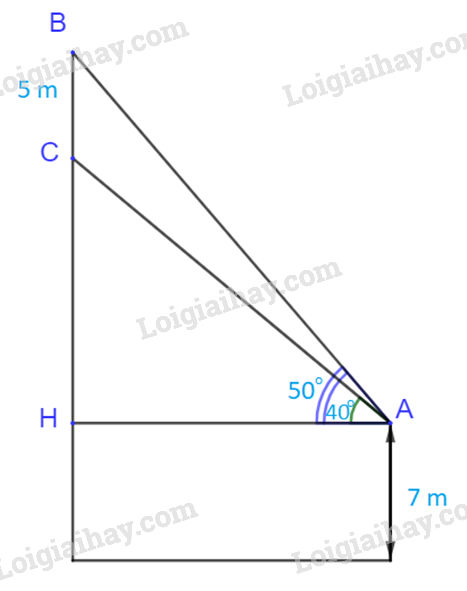
Bài 3.8 trang 42 Toán lớp 10 Tập 1 | Kết nối tri thức (ảnh 2)

Gọi H là hình chiếu của A lên đường thẳng BC.

Ta có: $\hat{H A B} = 50^{o}$ ; $\hat{H A C} = 40^{o}$

$\Rightarrow \hat{B A C} = 50^{o} - 40^{o} = 10^{o}$ (1)

Xét tam giác ABH, vuông tại H ta có:

$\hat{H} = 90^{o}; \hat{B A H} = 50^{o} .$

$\Rightarrow \hat{H B A} = 180^{o} - 90^{o} - 50^{o} = 40^{o}$ hay $\hat{C B A} = 40^{o}$ . (2)

Từ (1) và (2), suy ra: $\hat{B C A} = 180^{o} - 40^{o} - 10^{o} = 130^{o} .$

Vậy ba góc của tam giác ABC lần lượt là: $\hat{A} = 10^{o}; \hat{B} = 40^{o}; \hat{C} = 130^{o}$ .

b) Tính chiều cao của tòa nhà.

Phương pháp giải:

Bước 1: Tính AB: $A B = \frac{B C . \sin C}{\sin A}$

Bước 2: Tính BH => chiều cao của tòa nhà = BH + độ cao của vị trí quan sát.

Lời giải:

Áp dụng định lý sin cho tam giác ABC, ta được:

$\frac{B C}{\sin A} = \frac{A C}{\sin B} = \frac{A B}{\sin C}$ $\Rightarrow A B = \frac{B C . \sin C}{\sin A}$

Mà: $B C = 5 (m); \hat{C} = 130^{o}; \hat{A} = 10^{o}$

$\Rightarrow A B = \frac{5. \sin 130^{o}}{\sin 10^{o}} \approx 22 (m)$

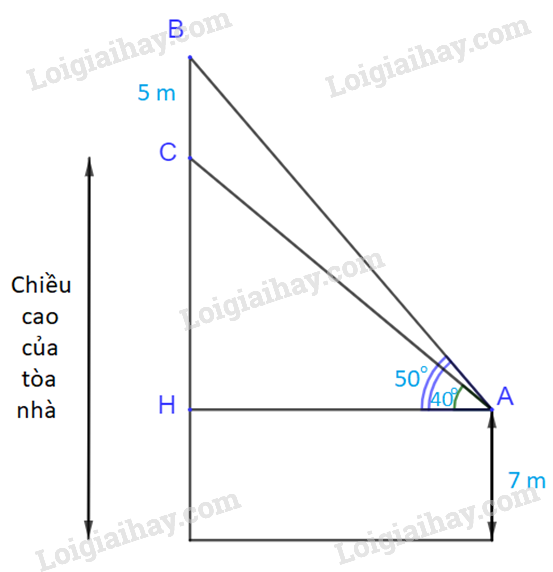
Bài 3.8 trang 42 Toán lớp 10 Tập 1 | Kết nối tri thức (ảnh 3)

Xét tam giác ABH, vuông tại H ta có:

$\sin \hat{B A H} = \frac{B H}{A B}$ $\Rightarrow B H = A B . \sin \hat{B A H}$

Mà: $A B \approx 22 (m); \hat{B A H} = 50^{o}$

$\Rightarrow B H \approx 22. \sin 50^{o} \approx 16, 85 (m)$

Vậy chiều cao của tòa nhà là: $B H - B C + 7 = 16, 85 - 5 + 7 = 18, 85 (m)$

Bài tập vận dụng:

Bài 1: Giải tam giác ABC biết AB = 15, BC = 35, $\hat{B} = 60 °$ . (Độ dài cạnh AC làm tròn đến chữ số thập phân thứ nhất, số đo góc A và C làm tròn đến độ).

Hướng dẫn giải

Áp dụng định lí côsin cho tam giác ABC, ta có:

AC² = AB² + BC² – 2. AB. BC . cos B

= 15² + 35² – 2. 15. 35. cos 60° = 925.

Do đó AC = $\sqrt{925}$ ≈ 30,4.

Mặt khác:

BC² = AB² + AC² – 2. AB. AC . cos A

⇒ cos A = $\frac{{AB}^{2} + {AC}^{2} - {BC}^{2}}{2. AB . AC}$ = $\frac{15^{2} + 925 - 35^{2}}{2.15. \sqrt{925}} \approx - 0, 08$ .

⇒ $\hat{A} \approx 95 °$

⇒ $\hat{C} = 180 ° - (\hat{A} + \hat{B}) \approx 180 ° - (95 ° + 60 °) = 25 °$

Vậy tam giác ABC có:

$\hat{A} \approx 95 °$ ; $\hat{B} = 60 °$ ; $\hat{C} \approx 25 °$ .

AB = 15, AC ≈ 30,4; BC = 35.

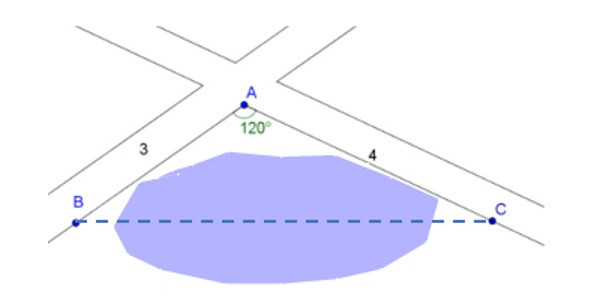
Bài 2: Một hồ nước nằm ở góc tạo bởi hai con đường. Hãy tính khoảng cách từ B đến C, biết góc tạo bởi hai con đường là góc A bằng 120° và khoảng cách từ A đến B là 3 km, khoảng cách từ A đến C là 4 km.

Hệ thức lượng trong tam giác (Lý thuyết + Bài tập Toán lớp 10) – Kết nối tri thức (ảnh 1)