Tailieumoi.vn xin giới thiệu Giải bài tập Toán 9 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có ngoài ở bên trong đường tròn hay, chi tiết giúp học sinh dễ dàng làm bài tập Góc có đỉnh ở bên trong đường tròn. Góc có ngoài ở bên trong đường tròn lớp 9.

Giải bài tập Toán lớp 9 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có ngoài ở bên trong đường tròn

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 81 SGK Toán lớp 9 Tập 2: Hãy chứng minh định lí: Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.

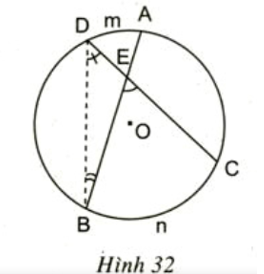
Gợi ý: Xem hình 32. Sử dụng góc ngoài của tam giác, chứng minh:

$\mathrm{BEC}=\frac{\mathrm{s}\text{d }\stackrel{⏜}{\text{BnC}}+\mathrm{sd}\stackrel{⏜}{\mathrm{AmD}}}{2}$

Lời giải:

Xét đường tròn (O) có:

Góc BDC là góc nội tiếp chắn cung BnC

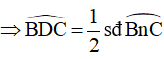
Góc DBA là góc nội tiếp chắn cung DmA 

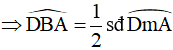
Xét tam giác BDE có:

Góc BEC là góc ngoài tại đỉnh E

Xét đường tròn (O) có:

Góc BDC là góc nội tiếp chắn cung BnC sđ

Góc DBA là góc nội tiếp chắn cung DmA sđ

Xét tam giác BDE có:

Góc BEC là góc ngoài tại đỉnh E

$$\begin{gathered} \Rightarrow \widehat{BEC}=\widehat{CDB}+ \widehat{ADB} \\ =\frac{1}{2}sđ \stackrel{⏜}{BnC}+\frac{1}{2}sđ\stackrel{⏜}{DmA} \\ =\frac{1}{2}(sđ\stackrel{⏜}{BnC}+ sđ\stackrel{⏜}{DmA}) \left(đpcm\right) \end{gathered}$$

Câu hỏi 2 trang 82 SGK Toán lớp 9 Tập 2: Hãy chứng minh định lí: Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.

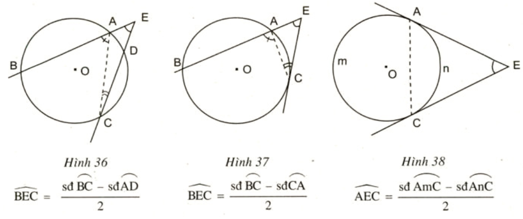
Gợi ý: Sử dụng góc ngoài của tam giác trong ba trường hợp ở hình 36, 37, 38 (các cung nêu ra dưới hình là những cung bị chắn).

Lời giải:

TH1: Hình 36

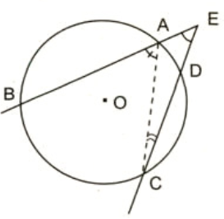
Xét đường tròn (O):

Góc BAC là góc nội tiếp chắn cung nhỏ BC của đường tròn (O)

Góc ACE là góc nội tiếp chắn cung nhỏ AD của đường tròn (O)

Xét tam giác AEC có:

Góc BAC là góc ngoài tại đỉnh A

TH2: Hình 37

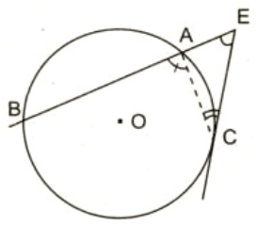
Xét đường tròn (O):

Góc BAC là góc nội tiếp chắn cung nhỏ BC của đường tròn (O)

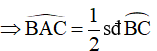
Góc ACE là góc nội tiếp chắn cung nhỏ AC của đường tròn (O)

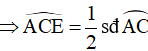
Xét tam giác AEC có:

Góc BAC là góc ngoài tại đỉnh A

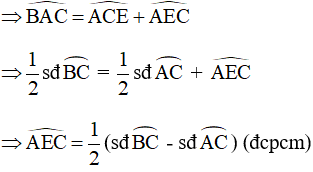
TH3: Hình 38

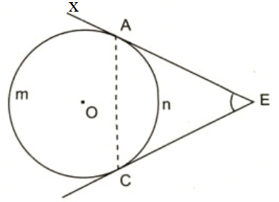
Góc CAx là góc tạo bởi tiếp tuyến Ax và dây cung AC chắn cung AmC của đường tròn (O)

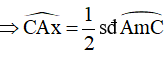
Góc ACE là góc nội tiếp chắn cung AnC của đường tròn (O)

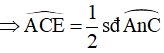
Xét tam giác ACE có:

Góc CAx là góc ngoài tại đỉnh A

Bài tập (trang 82)

Bài 36 trang 82 SGK Toán lớp 9 Tập 2: Cho đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của cung AB và cung AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh tam giác AEH là tam giác cân.

Lời giải:

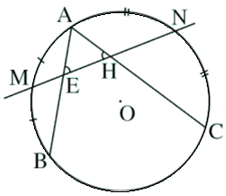
Xét đường tròn (O)

Góc AEN là góc có đỉnh nằm trong đường tròn (O)

Góc AHM là góc có đỉnh nằm trong đường tròn (O)

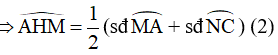
Theo giả thiết ta có:

M là điểm chính giữa cung AB

N là điểm chính giữa cung AC

Từ (1), (2), (3) và (4) ta suy ra: $\widehat{AEN}=\widehat{AHM}$

Xét tam giác AEH có: $\widehat{AEN}=\widehat{AHM}$

Do đó, tam giác AEH cân tại A.

Bài 37 trang 82 SGK Toán lớp 9 Tập 2:Cho đường tròn (O) và hai dây AB, AC bằng nhau. Trên cung nhỏ AC lấy một điểm M. Gọi S là giao điểm của AM và BC. Chứng minh .

Lời giải:

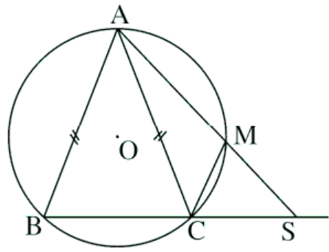
Xét đường tròn (O)

Góc ASC là góc có đỉnh nằm ngoài đường tròn (O)

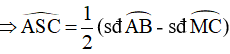
Theo giả thiết, ta có: AB = AC

Mà dây AB chắn cung AB, dây AC chắn cung AC

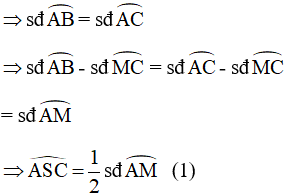
Mặt khác, ta lại có: Góc MCA là góc nội tiếp chắn cung AM

Từ (1) và (2) ta suy ra: $\widehat{ASC}=\widehat{MCA}$

Xét tam giác BAC có:

$\widehat{ASC}=\widehat{MCA}$ (đcpcm)

Bài 38 trang 82 SGK Toán lớp 9 Tập 2: Trên một đường tròn, lấy liên tiếp ba cung AC, CD, DB sao cho sđ$\stackrel{⏜}{AC}$= sđ$\stackrel{⏜}{CD}$ = sđ$\stackrel{⏜}{DB}$= ${60}^0$. Hai đường thẳng AC và BD cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:

a) $\widehat{AEB}=\widehat{BTC}$;

b) CD là tia phân giác của $\widehat{BCT}$.

Lời giải:

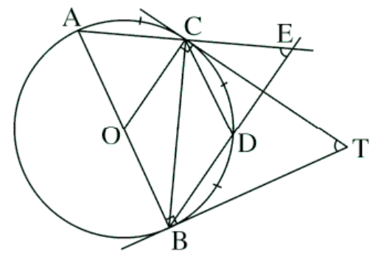
a)

Ta có: AB là đường kính của (O)

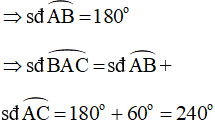
Mặt khác ta có: 

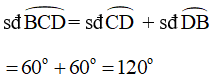
Góc BTC là góc có đỉnh nằm bên ngoài đường tròn (O) nên ta có:

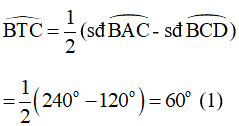
Góc AEB là góc có đỉnh nằm bên ngoài đường tròn (O) nên ta có:

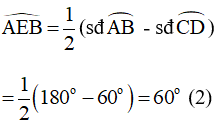
Từ (1) và (2) ta suy ra: $\widehat{BTC}=\widehat{AEB}$ (đcpcm)

b)

Góc DCT là góc tạo bởi tiếp tuyến CT và dây cung CD của (O)

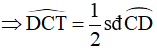
Lại có: Góc BCD là góc nội tiếp chắn cung CB của (O)

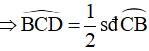
Mà

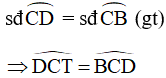
Do đó, CD là tia phân giác của góc BCT .

Luyện tập trang 83

Bài 39 trang 83 SGK Toán lớp 9 Tập 2: Cho AB và CD là hai đường kính vuông góc của đường tròn (O). Trên cung nhỏ BD lấy một điểm M. Tiếp tuyến tại M cắt tia AB ở E, đoạn thẳng CM cắt AB ở S. Chứng minh ES = EM.

Lời giải:

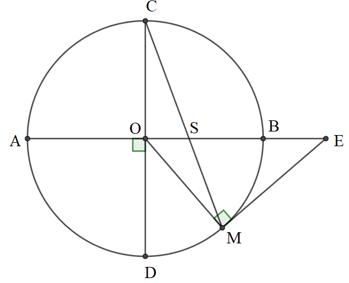
AB, CD là hai đường kính vuông góc

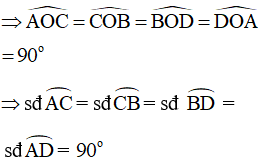
Ta có:

Góc EMS là góc tạo bởi tia tiếp tuyến ME và dây cung MC

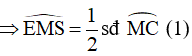
Góc BSM là góc có đỉnh nằm trong đường tròn (O) nên ta có:

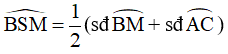
Mà: sđ $\stackrel{⏜}{AC}$= sđ $\stackrel{⏜}{CB}$ (chứng minh trên)

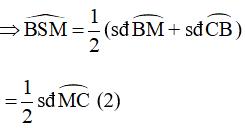
Từ (1) và (2) ta suy ra:  $\widehat{EMS}=\widehat{BSM}$

Xét tam giác ESM có: $\widehat{EMS}=\widehat{BSM}$

Do đó, tam giác ESM cân tại E

$\Rightarrow$ES = EM.

Bài 40 trang 83 SGK Toán lớp 9 Tập 2: Qua điểm S nằm bên ngoài đường tròn (O), vẽ tiếp tuyến SA và cắt cát tuyến SBC của đường tròn . Tia phân giác của góc BAC cắt dây BC tại D. Chứng minh SA = SD.

Lời giải:

Xét đường tròn (O)

Góc SAE là góc tạo bởi tia tiếp tuyến SA và dây cung AE

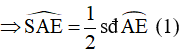
Góc ADS là góc có đỉnh nằm bên trong (O) 

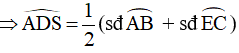
Ta có: AE là tia phân giác của góc BAC (gt)

Mà góc BAD là góc nội tiếp chắn cung BE, góc DAC là góc nội tiếp chắn cung EC

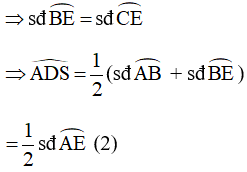
Từ (1) và (2) ta suy ra: $\widehat{SAE}=\widehat{ADS}$ hay $\widehat{SAD}=\widehat{ADS}$

Xét tam giác SAD có: $\widehat{SAD}=\widehat{ADS}$

Do đó, tam giác SAD cân tại S

$\Rightarrow SA=SD$ (đcpcm).

Bài 41 trang 83 SGK Toán lớp 9 Tập 2: Qua điểm A nằm bên ngoài đường tròn (O) vẽ hai cát tuyến ABC và AMN sao cho hai đường thẳng BN và CM cắt nhau tại một điểm S nằm bên tròn đường tròn. Chứng minh: $\widehat{A}+\widehat{BSM}=2\widehat{CMN}$.

Lời giải:

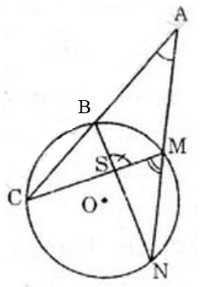
Xét đường tròn (O):

Góc A là góc có đỉnh nằm ngoài (O) chắn hai cung BM và CN

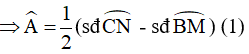
Góc BSM là góc có đỉnh nằm trong (O) chắn hai cung BM và CN

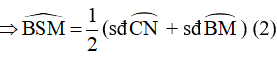
Từ (1) và (2) ta suy ra:

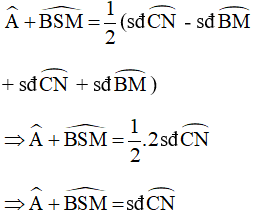
Mà: Góc CMN là góc nội tiếp chắn cung CN

Bài 42 trang 83 SGK Toán lớp 9 Tập 2:Cho tam giác ABC nội tiếp đường tròn. P, Q, R theo thứ tự là các điểm chính giữa của các cung bị chắn BC, CA, AB bởi các góc A, B, C.

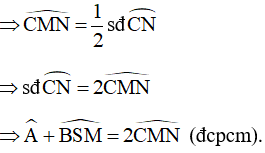
a) Chứng minh $\mathrm{AP}\perp \mathrm{QR}$

b) AP cắt CR tại I. Chứng minh tam giác CPI là tam giác cân.

Lời giải:

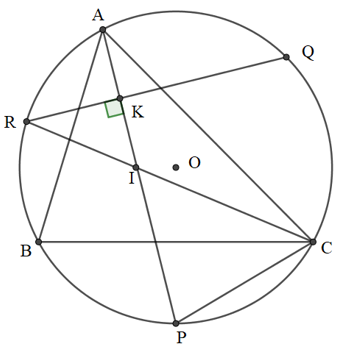
a)

Gọi K là giao điểm của AP và QR.

P là điểm chính giữa cung BC

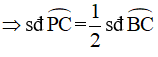
Q là điểm chính giữa cung AC 

R là điểm chính giữa cung AB

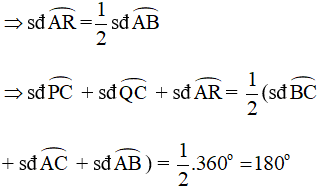
Xét đường tròn (O) ta có:

Góc AKR là góc có đỉnh bên trong đường tròn chắn hai cung AB và QP

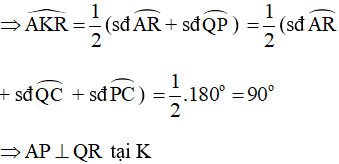
b)

Xét đường tròn (O) ta có:

Góc CIP là góc có đỉnh ở bên trong đường tròn chắn hai cung AR và CP

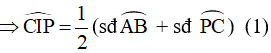
Góc PCI là góc nội tiếp chắn cung PR nên ta có:

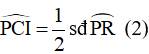
Theo giả thiết ta có:

R là điểm chính giữa cung AB

$\Rightarrow \stackrel{⏜}{AR}=\stackrel{⏜}{RB}$ (3)

P là điểm chính giữa cung BC

$\Rightarrow \stackrel{⏜}{CP}=\stackrel{⏜}{BP}$ (4)

Từ (1), (2), (3) và (4) ta có: $\widehat{CIP}=\widehat{PCI}$

Xét tam giác CPI có: $\widehat{CIP}=\widehat{PCI}$

Do đó , tam giác CPI cân tại P.

Bài 43 trang 83 SGK Toán lớp 9 Tập 2:Cho đường tròn (O) và hai dây cung song song AB, CD (A và C nằm trong cùng một nửa mặt phẳng bờ BD); AD cắt BC tại I. Chứng minh $\widehat{AOC}=\widehat{AIC}$.

Lời giải:

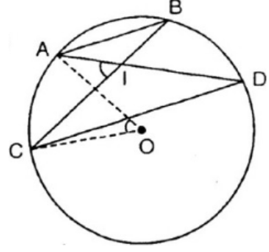
Xét đường tròn (O)

Do AB // CD (gt) nên ta có: $\stackrel{⏜}{AC}=\stackrel{⏜}{BD}$ (1) (tính chất 2 dây cung song song căng 2 cung bằng nhau).    

Góc AIC là góc có đỉnh bên trong (O) chắn hai cung AC và BD

Từ (1) và (2) ta suy ra: 

Mà góc AOC là góc ở tâm chắn cung AC