Với giải Bài 38 trang 82 Toán lớp 9 chi tiết trong Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có ngoài ở bên trong đường tròn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán lớp 9 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có ngoài ở bên trong đường tròn
Bài 38 trang 82 SGK Toán lớp 9 Tập 2: Trên một đường tròn, lấy liên tiếp ba cung AC, CD, DB sao cho sđ= sđ = sđ= . Hai đường thẳng AC và BD cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:
a) ;
b) CD là tia phân giác của .
Lời giải:
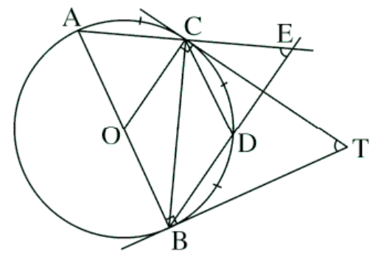
a)
Ta có: AB là đường kính của (O)
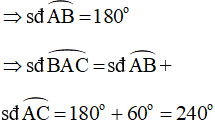
Mặt khác ta có:
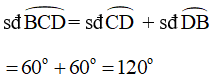
Góc BTC là góc có đỉnh nằm bên ngoài đường tròn (O) nên ta có:
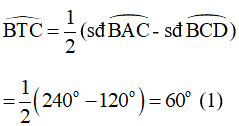
Góc AEB là góc có đỉnh nằm bên ngoài đường tròn (O) nên ta có:
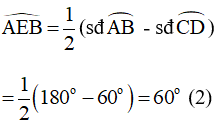
Từ (1) và (2) ta suy ra: (đcpcm)
b)
Góc DCT là góc tạo bởi tiếp tuyến CT và dây cung CD của (O)
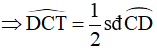
Lại có: Góc BCD là góc nội tiếp chắn cung CB của (O)
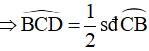
Mà
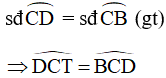
Do đó, CD là tia phân giác của góc BCT .
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
