Với giải Bài 42 trang 83 Toán lớp 9 chi tiết trong Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có ngoài ở bên trong đường tròn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán lớp 9 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có ngoài ở bên trong đường tròn

Bài 42 trang 83 SGK Toán lớp 9 Tập 2:Cho tam giác ABC nội tiếp đường tròn. P, Q, R theo thứ tự là các điểm chính giữa của các cung bị chắn BC, CA, AB bởi các góc A, B, C.

a) Chứng minh $\mathrm{AP}\perp \mathrm{QR}$

b) AP cắt CR tại I. Chứng minh tam giác CPI là tam giác cân.

Lời giải:

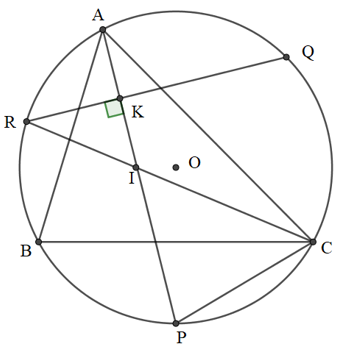
a)

Gọi K là giao điểm của AP và QR.

P là điểm chính giữa cung BC

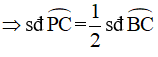
Q là điểm chính giữa cung AC 

R là điểm chính giữa cung AB

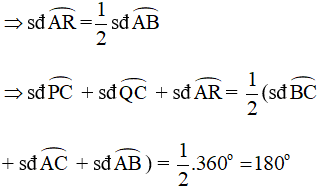
Xét đường tròn (O) ta có:

Góc AKR là góc có đỉnh bên trong đường tròn chắn hai cung AB và QP

b)

Xét đường tròn (O) ta có:

Góc CIP là góc có đỉnh ở bên trong đường tròn chắn hai cung AR và CP

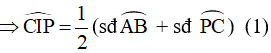
Góc PCI là góc nội tiếp chắn cung PR nên ta có:

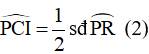
Theo giả thiết ta có:

R là điểm chính giữa cung AB

$\Rightarrow \stackrel{⏜}{AR}=\stackrel{⏜}{RB}$ (3)

P là điểm chính giữa cung BC

$\Rightarrow \stackrel{⏜}{CP}=\stackrel{⏜}{BP}$ (4)

Từ (1), (2), (3) và (4) ta có: $\widehat{CIP}=\widehat{PCI}$

Xét tam giác CPI có: $\widehat{CIP}=\widehat{PCI}$

Do đó , tam giác CPI cân tại P.