Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh bộ câu hỏi trắc nghiệm Toán lớp 9 Bài 5: Góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn chọn lọc, có đáp án. Tài liệu có 24 trang gồm 30 câu hỏi trắc nghiệm cực hay bám sát chương trình sgk Toán 9. Hi vọng với bộ câu hỏi trắc nghiệm Góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn có đáp án này sẽ giúp bạn ôn luyện trắc nghiệm để đạt kết quả cao trong bài thi trắc nghiệm môn Toán 9.

Giới thiệu về tài liệu:

- Số trang: 24 trang

- Số câu hỏi trắc nghiệm: 30 câu

- Lời giải & đáp án: có

Mời quí bạn đọc tải xuống để xem đầy đủ tài liệu Trắc nghiệm Góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn có đáp án – Toán lớp 9:

Góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn

Câu 1: Cho hình vẽ dưới đây, góc BIC có số đo bằng:

Lời giải:

Số đo góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn

Đáp án cần chọn là: B

Câu 2: Góc có đỉnh bên ngoài đường tròn có số đo

A. Bằng nửa hiệu số đo hai cung bị chắn

B. Bằng nửa tổng số đo hai cung bị chắn

C. Bằng số đo cung lớn bị chắn

D. Bằng số đo cung nhỏ bị chắn

Lời giải:

Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn

Đáp án cần chọn là: A

Câu 3: Cho hình vẽ dưới đây, góc DIE có số đo bằng

Lời giải:

Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn

Đáp án cần chọn là: A

Câu 4: Góc có đỉnh bên trong đường tròn có số đo:

A. Bằng nửa hiệu số đo hai cung bị chắn

B. Bằng nửa tổng số đo hai cung bị chắn

C. Bằng số đo cung lớn bị chắn

D. Bằng số đo cung nhỏ bị chắn

Lời giải:

Số đo góc có đỉnh bên trong đường tròn có số đo bằng nửa tổng số đo hai cung bị chắn

Đáp án cần chọn là: B

Câu 5: Cho nửa đường tròn (O) đường kính AB và C là điểm trên cung nhỏ AB (cung CB nhỏ hơn cung CA). Tiếp tuyến tại C của nửa đường tròn cắt đường thẳng AB tại D. Biết tam giác ADC cân tại C. Tính góc ADC

A. 40^o         

B. 45^o         

C. 60^o         

D. 30^o

Lời giải:

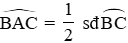
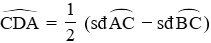
Xét nửa (O) có   (góc nội tiếp chắn cung BC) và  (góc có đỉnh bên ngoài đường tròn)

Đáp án cần chọn là: D

Câu 6: Cho đường tròn (O) và điểm E nằm ngoài đường tròn. Vẽ cát tuyến EAB và ECD với đường tròn (A nằm giữa E và B, C nằm giữa E và D). Gọi F là một điểm trên đường tròn sao cho B nằm chính giữa cung DF, I là giao điểm của FA và BC. Biết 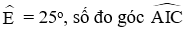 là:

A. 20^o         

B. 50^o         

C. 25^o         

D. 30^o

Lời giải:

B nằm chính giữa cung DF nên 

Mặt khác góc tại E và I là hai góc có đỉnh bên ngoài đường tròn nên

Đáp án cần chọn là: C

Câu 7: Trên (O) lấy bốn điểm A, B, C, D theo thứ tự sao cho cung AB = cung BC = cung CD. Gọi I là giao điểm của BD và AC, biết 

A. 20^o         

B. 15^o         

C. 35^o         

D. 30^o

Lời giải:

Vì cung AB = cung BC = cung CD nên gọi số đo mỗi cung là a độ. Ta có số đo cung AD là 360^o – 3a

Vì 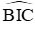  là góc có đỉnh bên trong đường tròn nên:

Đáp án cần chọn là: B

Câu 8: Trên (O) lấy bốn điểm A, B, C, D theo thứ tự sao cho cung AB = cung BC = cung CD. Gọi I là giao điểm của BD và AC, biết 

A. 20^o         

B. 15^o         

C. 35^o         

D. 30^o

Lời giải:

Vì cung AB = cung BC = cung CD nên gọi số đo mỗi cung là a độ. Ta có số đo cung AD là 360^o – 3a

Vì 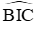  là góc có đỉnh bên trong đường tròn nên:

Đáp án cần chọn là: D

Câu 9: Cho (O; R) và dây AB bất kỳ. Gọi M là điểm chính giữa cung nhỏ AB; E, F là hai điểm bất kì trên dây AB. Gọi C, D lần lượt là giao điểm của ME, MF với (O). Khi đó 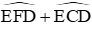 bằng

A. 180^o      

B. 150^o       

C. 135^o       

D. 120^o

Lời giải:

Ta có  là góc có đỉnh bên trong đường tròn nên  

Đáp án cần chọn là: A

Câu 10: Cho (O; R) và dây AB bất kỳ. Gọi M là điểm chính giữa cung nhỏ AB; E, F là hai điểm bất kì trên dây AB. Gọi C, D lần lượt là giao điểm của ME, MF với (O). Khi đó 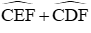 bằng:

A. 180^o      

B. 150^o       

C. 145^o       

D. 180^o

Lời giải:

Ta có  là góc có đỉnh bên trong đường tròn nên  

Đáp án cần chọn là: D

Câu 11: Cho (O; R) có hai đường kính AB, CD vuông góc với nhau. Gọi M là điểm chính giữa cung BC. Dây AM cắt OC tại E, dây CM cắt đường thẳng AB tại N. Tam giác MCE là tam giác gì?

A. ∆MEC cân tại E                          

B. ∆MEC cân tại M

C. ∆MEC cân tại C                           

D. ∆MEC đều

Lời giải:

Xét (O) có 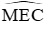 là góc có đỉnh bên trong đường tròn nên

Mà cung MB = cung MC và cung AD = cung BD

Từ đó 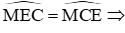 ⇒ ∆MEC cân tại M

Đáp án cần chọn là: B

Vận dụng: Cho (O; R) có hai đường kính AB, CD vuông góc với nhau. Gọi M là điểm chính giữa cung BC. Dây AM cắt OC tại E, dây CM cắt đường thẳng AB tại N. Hai đoạn thẳng nào sau đây bằng nhau?

A. BN; BC 

B. BN; NC 

C. BC; NC 

D. BC; OC

Lời giải:

Xét (O) 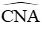 là góc có đỉnh bên ngoài đường tròn nên  

Đáp án cần chọn là: A

Vận dụng: Cho (O; R) có hai đường kính AB, CD vuông góc với nhau. Gọi M là điểm chính giữa cung BC. Dây AM cắt OC tại E, dây CM cắt đường thẳng AB tại N. Tính diện tích tam giác CBN theo R

Lời giải:

Đáp án cần chọn là: B

Câu 12: Cho (O; R) có hai đường kính AB, CD vuông góc với nhau. Gọi M là điểm chính giữa cung BC. Dây AM cắt OC tại E, dây CM cắt đường thẳng AB tại N. Số đo góc MEC bằng:

A. 68^o         

B. 70^o         

C. 60^o         

D. 67,5^o

Lời giải:

Vì hai đường kính AB và CD vuông góc với nhau nên

Xét (O) có 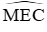 là góc có đỉnh bên trong đường tròn nên

Đáp án cần chọn là: D

Vận dụng: Cho (O; R) có hai đường kính AB, CD vuông góc với nhau. Gọi M là điểm chính giữa cung BC. Dây AM cắt OC tại E, dây CM cắt đường thẳng AB tại N. Số đo góc CNA bằng:

A. 45^o         

B. 30^o         

C. 22,5^o      

D. 67,5^o

Lời giải:

Xét (O) có 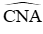 là góc có đỉnh bên ngoài đường tròn nên

Đáp án cần chọn là: C

Vận dụng: Cho (O; R) có hai đường kính AB, CD vuông góc với nhau. Gọi M là điểm chính giữa cung BC. Dây AM cắt OC tại E, dây CM cắt đường thẳng AB tại N. Tính diện tích tam giác CON theo R

Lời giải:

Xét (O) có 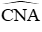 là góc có đỉnh bên ngoài đường tròn nên

Lại có 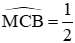  số đo cung MB (góc nội tiếp) nên:

Đáp án cần chọn là: A

Câu 13: Từ A ở ngoài (O) vẽ tiếp tuyến AB và cát tuyến ACD. Tia phân giác 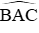 cắt BC, BD lần lượt tại M, N. Vẽ dây BF vuông góc với MN tại H và cắt CD tại E. Tam giác BMN là tam giác gì?

A. ∆BMN cân tại N                                   

B. ∆BMN cân tại M

C. ∆BMN cân tại B                                   

D. ∆BMN đều

Lời giải:

Xét (O) có đường thẳng AM cắt đường tròn tại I; K. Khi đó:

Đáp án cần chọn là: C

Vận dụng: Từ A ở ngoài (O) vẽ tiếp tuyến AB và cát tuyến ACD. Tia phân giác 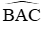 cắt BC, BD lần lượt tại M, N. Vẽ dây BF vuông góc với MN tại H và cắt CD tại E. Tích FE. FB bằng:

A. BE²       

B. BF²        

C. DB²       

D. FD²

Lời giải:

Xét (O) có đường thẳng AM cắt đường tròn tại I; K. Khi đó:

Vì tam giác BMN cân tại B có BH là đường cao nên BH cũng là đường phân giác

Đáp án cần chọn là: D

Câu 14: Trên đường tròn (O; R) vẽ ba dây liên tiếp bằng nhau AB = BC = CD, mỗi dây có độ dài nhỏ hơn R. Các đường thẳng AB, CD cắt nhau tại I, các tiếp tuyến của (O) tại B và D cắt nhau tại K. Góc BIC bằng góc nào dưới đây?

Lời giải:

Đáp án cần chọn là: B

Vận dụng: Trên đường tròn (O; R) vẽ ba dây liên tiếp bằng nhau AB = BC = CD, mỗi dây có độ dài nhỏ hơn R. Các đường thẳng AB, CD cắt nhau tại I, các tiếp tuyến của (O) tại B và D cắt nhau tại K.BC là tia phân giác của góc nào dưới đây?

Lời giải:

Xét (O) có 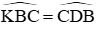 (hệ quả góc tạo bởi tiếp tuyến và dây cung)

Lại có 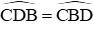 (hai góc nội tiếp chắn hai cung bằng nhau)

Nên 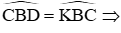 BC là tia phân giác góc KBD

Đáp án cần chọn là: A

Câu 15: Cho tam giác nhọn ABC nội tiếp (O). Các tiếp tuyến tại B, C của (O) cắt nhau tại M. Biết 

A. 45^o         

B. 50^o         

C. 72^o         

D. 120^o

Lời giải:

Xét (O) có: 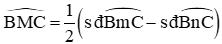 (góc có đỉnh bên ngoài đường tròn)

Đáp án cần chọn là: C

Câu 16: Cho tam giác nhọn ABC nội tiếp (O). Các tiếp tuyến tại B, C của (O) cắt nhau tại M. Biết 

A. 36^o         

B. 72^o         

C. 60^o         

D. 120^o

Lời giải:

Xét (O) có: 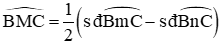 (góc có đỉnh bên ngoài đường tròn)

Đáp án cần chọn là: A

Câu 17: Cho đường tròn (O) và một dây AB. Vẽ đường kính CD ⊥ AB (D thuộc cung nhỏ AB). Trên cung nhỏ BC lấy điểm M. Các đường thẳng CM, DM cắt đường thẳng AB lần lượt tại E và F. Tiếp tuyến của đường tròn tại M cắt đường thẳng AB tại N. Hai đoạn thẳng nào dưới đây không bằng nhau?

A. NM; NE

B. NM; NF 

C. NE; NF  

D. EN; AE

Lời giải:

Xét (O) có D là điểm chính giữa cung AB (Vì đường kính CD ⊥ AB nên đi qua điểm chính giữa cung AB)

 (góc tạo bởi tiếp tuyến và dây cung)

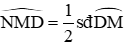
Đáp án cần chọn là: D

Câu 18: Cho (O; R) có hai đường kính AB, CD vuông góc với nhau. Trên đường kính AB lấy điểm E sao cho AE = R√2. Vẽ dây CF đi qua E. Tiếp tuyến của đường tròn tại F cắt đường thẳng CD tại M, dây AF cắt CD tại N. Chọn khẳng định sai.

A. AC // MF                            

B. ∆ACE cân tại A

C. ∆ABC cân tại C                 

D. AC // FD

Lời giải:

Mà hai góc ở vị trí so le trong nên AC // MF

Xét tam giác CAB có CO là đường trung trực của AB nên ∆ACB cân tại C

Phương án A, B, C đúng

Đáp án cần chọn là: D

Câu 19: Cho (O; R) có hai đường kính AB, CD vuông góc với nhau. Trên đường kính AB lấy điểm E sao cho AE = R√2. Vẽ dây CF đi qua E. Tiếp tuyến của đường tròn tại F cắt đường thẳng CD tại M, dây AF cắt CD tại N. Tính độ dài ON theo R

Lời giải:

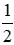
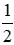
Hay (số đo cung AD + số đo cung DF) = (số đo cung AC + số đo cung BF)

mà cung AD = cung AC nên cung DF = cung BF

Đáp án cần chọn là: C

Câu 20: Cho ABC nhọn nội tiếp đường tròn (O). Vẽ phân giác trong AD của góc A (D ≠ O). Lấy điểm E thuộc cung nhỏ AC. Nối BE cắt AD và AC lần lượt tại I và tại K, nối DE cắt AC tại J. Kết luận nào đúng?

Lời giải:

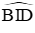
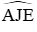
Ta có  là góc có đỉnh nằm trong đường tròn (O) chắn hai cung BD và AE

+)  là góc có góc có đỉnh nằm trong đường tròn (O) chắn cung CD và AE

Đáp án cần chọn là: A

Bài giảng Toán 9 Bài 5: Góc có đỉnh ở bên trong đường tròn góc có đính ở bên ngoài đường tròn