Với giải Bài 41 trang 83 Toán lớp 9 chi tiết trong Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có ngoài ở bên trong đường tròn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán lớp 9 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có ngoài ở bên trong đường tròn
Bài 41 trang 83 SGK Toán lớp 9 Tập 2: Qua điểm A nằm bên ngoài đường tròn (O) vẽ hai cát tuyến ABC và AMN sao cho hai đường thẳng BN và CM cắt nhau tại một điểm S nằm bên tròn đường tròn. Chứng minh: .
Lời giải:
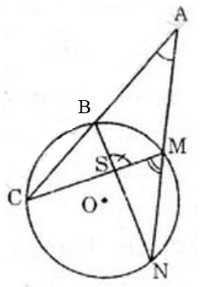
Xét đường tròn (O):
Góc A là góc có đỉnh nằm ngoài (O) chắn hai cung BM và CN
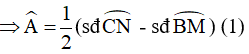
Góc BSM là góc có đỉnh nằm trong (O) chắn hai cung BM và CN
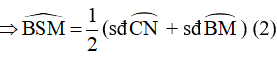
Từ (1) và (2) ta suy ra:
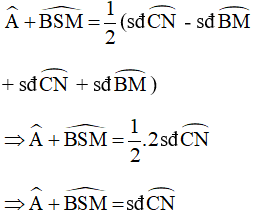
Mà: Góc CMN là góc nội tiếp chắn cung CN
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
